cs224w 图神经网络 学习笔记(八)Graph Representation Learning 图表示学习
课程链接:CS224W: Machine Learning with Graphs
课程视频:【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)
目录
-
- 1. 前言——Network Embedding
- 2. Embedding Nodes
-
- 2.1 Random Walk Approaches to Node Embeddings
- 2.2 Node2Vec
- 2.3 小结
- 3. Translating Embedding for Modeling Multi-relational Data——An Application of Embeddings to the Knowledge Graph
- 4. Embedding entire graph
1. 前言——Network Embedding
在图结构上进行机器学习的任务有节点分类、关系预测等。一本来说,有监督的机器学习都要经历以下几个步骤:首先在原始数据上进行特征工程,得到结构化的数据,接着确定机器学习算法,最终训练得到模型。在这个过程中,特征工程是十分耗时费力的。因此我们更喜欢能够自动获取这些特征的方式(如深度学习)。下面我们就来看一下基于图的特征学习(feature learning on graphs)。
基于图的特征学习的目标,是希望能够高效地完成机器学习过程中基于图的特征工程。如下图所示,通常会将节点表示成一个特征向量,向量的维度表示包含信息的多少。
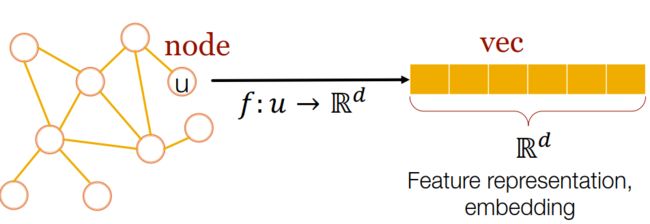
Network Embedding类似于NLP中的word embedding,主要任务是将网络中的每个节点映射到低维空间中。

Network Embedding有以下特点:
- embedding后的向量是节点的分布式表示
- 节点间embedding向量的相似度表示节点间的网络(结构)相似度
- 可以通过编码网络节点信息生成节点表示
下面是一个案例,将左边的图结构的节点用一个二维向量来表示(当然在实际项目中,embedding向量通常会有几十甚至几百个维度,这里采用二维向量只是为了方便可视化)。可以看到,在右边的图上,比较接近的点在网络中的关系也比较紧密。

但是,传统的深度学习框架很难解决Network Embedding,主要原因有以下几点:
- CNN用于固定大小的图像/网格,即像素点的拓扑结构使单一的、固定的。

- RNNs或word2vec用于文本/序列,即节点的次序是固定的。

- 而网络(Networks)的结构要复杂的多得多!网络拥有更加复杂的拓扑结构,且节点的顺序并不是固定的。更有甚者,网络是动态变化的。
因此,我们接下来讨论网络中的embedding nodes。
2. Embedding Nodes
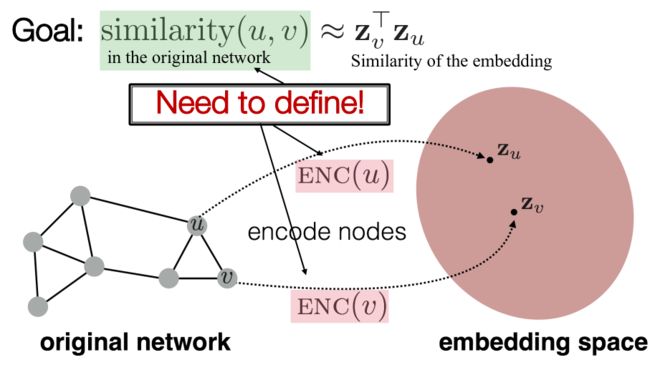
假设有图 G G G, V V V表示节点集合, A A A为邻接矩阵,Embedding Nodes的目标就是对节点进行编码,使Embedding向量空间中两个节点的相似性(例如,点积)近似于原始网络中两个节点的相似性。
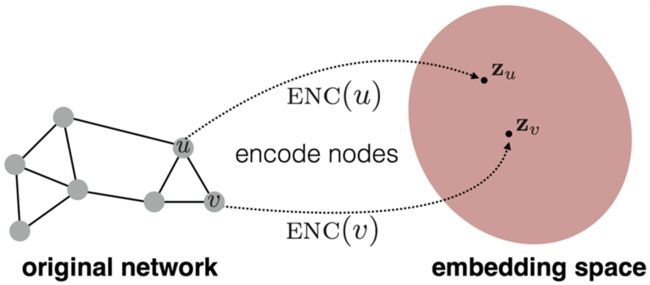
因此,我们的目标就是:
s i m i l a r i t y ( u , v ) ≈ z v T z u similarity(u,v) \approx {z}_v^{T}z_u similarity(u,v)≈zvTzu
(1)首先,定义一个编码器(从节点到嵌入向量的映射)。 E N C ( v ) = z v ENC(v)=z_v ENC(v)=zv, v v v表示图中的节点, z v z_v zv是一个 d d d维向量。最简单的编码器就是一个embedding-lookup,即 E N C ( v ) = Z v ENC(v)=Zv ENC(v)=Zv,其中 Z Z Z为 d × ∣ V ∣ d \times |V| d×∣V∣的矩阵,每一列都对应一个node embedding,这是我们需要学习的参数; v v v是一个 ∣ V ∣ |V| ∣V∣维的向量,节点编码的one-hot表示。这个方法中,每个节点被分配到一个唯一的嵌入向量。这是最简单的一个方法,后面会介绍更新的一些方法——DeepWalk, node2vec, TransE。
(2)其次,定义一个节点相似性函数(对原始网络节点相似度的计算函数),即 s i m i l a r i t y ( u , v ) similarity(u,v) similarity(u,v)。不同node embedding方法的核心区别在于他们怎么定义节点相似度。
(3)不断学习来优化编码器的参数,优化的目标是 s i m i l a r i t y ( u , v ) ≈ z v T z u similarity(u,v) \approx z_v^{T}z_u similarity(u,v)≈zvTzu。
2.1 Random Walk Approaches to Node Embeddings
首先,什么是random walk(随机游走)?给定一个图形和一个起点,我们随机选择它的一个邻居,并移动到这个邻居;然后我们随机选择这个点的一个邻居,然后移动到它那里,等等。以这种方式选择的(随机)点序列是在图上的随机游走。
那么 z v T z u z_v^{T}z_u zvTzu约等于节点 u u u和节点 v v v在网络随机游走中同时出现的概率。
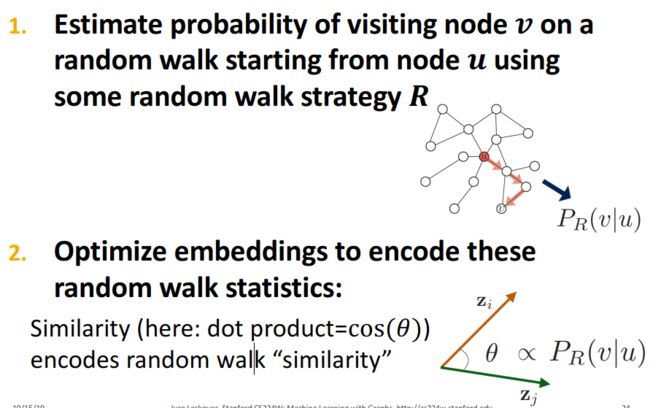
Random Walk算法有两个优势:
(1)表达性——节点相似计算的定义是灵活的、随机,包含了局部和高阶邻域信息
(2)效率高——训练时不需要考虑所有节点对;只需要考虑随机游动中同时发生的对
非监督的特征学习
非监督的特征学习的目标是希望能够将节点的one-hot向量embedded到一个 d d d维的向量空间,并能尽可能地保留节点之间的相似度。主要的思想在于学习node embedding ,使网络中邻近的节点更靠近。

给定图 G = ( V , E ) G=(V,E) G=(V,E),学习一种映射 z : u → R d z:u \to \Bbb{R}^d z:u→Rd,目标函数是似然函数 max z ∑ u ∈ V log P ( N R ( u ) ∣ z u ) \max_{z} \sum_{u \in V}\log P(N_R(u)|z_u) maxz∑u∈VlogP(NR(u)∣zu),这里的 N R ( u ) N_R(u) NR(u)是根据策略 R R R得到的节点 u u u的邻居。即给定节点 u u u,我们希望学习能够预测其邻居节点 N R ( u ) N_R(u) NR(u)的特征表示。
Random Walk Optimization
- 使用某种策略 R R R(如步长、random walk的次数等)从图上的每个节点开始进行短的固定长度的random walks。
- 对于每个节点 u u u,得到其在策略 R R R下的领域 N R ( u ) N_R(u) NR(u),需要注意的是 N R ( u ) N_R(u) NR(u)可以包含重复的节点,因为这些节点可以在random walk时被随机地重复访问。
- 根据最大似然函数(即上面提到的式子)对嵌入向量进行优化: max z ∑ u ∈ V log P ( N R ( u ) ∣ z u ) \max_{z} \sum_{u \in V}\log P(N_R(u)|z_u) maxz∑u∈VlogP(NR(u)∣zu)。
为此,我们可以得到损失函数:
L = ∑ u ∈ V ∑ v ∈ N R ( u ) − log ( P ( v ∣ z u ) ) \mathcal{L}=\sum_{u \in V} \sum_{v \in N_R(u)} - \log (P(v|z_u)) L=u∈V∑v∈NR(u)∑−log(P(v∣zu))

这里加了一个负号,即求最大似然函数最大值,相当于求损失函数的最小值。损失函数中概率相关的参数 P ( v ∣ z u ) P(v|z_u) P(v∣zu)通过softmax得到:
P ( v ∣ z u ) = e x p ( z u T z v ) ∑ n ∈ V e x p ( z u T z n ) P(v|z_u)=\frac {exp(z_u^T z_v)}{\sum_{n \in V} exp(z_u^T z_n)} P(v∣zu)=∑n∈Vexp(zuTzn)exp(zuTzv)
然而,新的问题出现了,要计算这个损失函数,其复杂度达到了 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2),导致复杂度这么高的主要原因在于softmax计算。解决方案是Negative Sampling。
Negative Sampling

Negative Sampling并非对所有节点执行归一化操作,而是随机选择 k k k个负样本进行归一化,其中 P V P_V PV是所有节点的随机分布。关于 k k k,有以下特点:
- k k k越大,估计的值越可靠;
- k k k越大,关于负样本的偏差就越大;
- 按照经验, k k k通常取5-20。
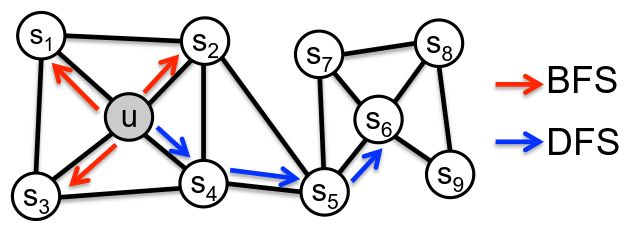
random walk的策略
最简单的想法——从每个节点开始进行固定长度的、没有偏差的random walk,参考论文DeepWalk from Perozzi et al., 2013,但是这种方法的问题在于对于相似度的定义太过于固定( The issue is that such notion of similarity is too constrained),无法检测到距离比较远但是相似度很高的节点。
2.2 Node2Vec
目标——使相似节点在特征空间中的embedded 向量尽可能地接近。我们将此目标看作一个最大似然优化问题,独立于下游的预测任务。为了解决上面random walk关于节点相似度定义的问题,Node2Vec将扩展节点 u u u的邻域 N R ( u ) N_R(u) NR(u)的定义,来丰富embedded nodes的信息。解决方案就是采用另一种random walk策略 R R R(biased 2 n d 2^{nd} 2nd order random walk R R R)来生成节点 u u u的邻域 N R ( u ) N_R(u) NR(u)。
Biased Walk
使用灵活的、有偏差的随机游动,可以在网络的局部和全局视图之间进行权衡(参考论文Grover and Leskovec, 2016)
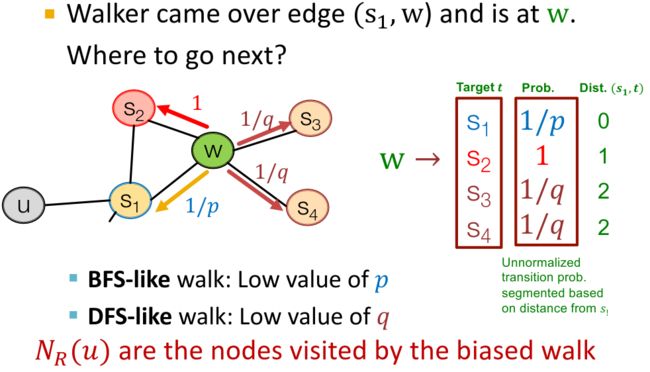
在该策略中,需要确定两个参数:
- Return parameter 返回参数 p p p——返回到上一个节点的概率
- In-out parameter q q q——Moving outwards (DFS) vs. inwards (BFS), q q q is the “ratio” of BFS vs. DFS。
例如:若节点进行BFS的概率为1,返回上一节点的概率为1/p,则进行DFS的概率为1/q(这里的概率是指未做归一化的概率)。这样的策略称为Biased Random Walks。——【CS224W课程笔记】Graph Representation Learning
(1)计算随机游走的概率
(2)模拟从每个节点 u u u开始的步长为 l l l的 r r r次随机游走
(3)利用随机梯度下降算法优化node2vec的目标(函数)。
Node2Vec算法的时间复杂度是线性的,且这三步是individually parallelizable的。
2.3 小结
How to use embeddings z i z_i zi of nodes?
训练好的节点嵌入向量可以应用于很多场景:
- 聚类/社区检测——Cluster points z i z_i zi
- 节点分类——根据节点 i i i的嵌入向量 z i z_i zi预测类别标签 f ( z i ) f(z_i) f(zi)
- 关系预测——根据不同的向量操作 f ( z i , z j ) f(z_i,z_j) f(zi,zj)预测边 ( i , j ) (i,j) (i,j)。
| 操作 | 计算式 |
|---|---|
| Concatenate 连接 | f ( z i , z j ) = g ( [ z i , z j ] ) f(z_i,z_j)=g([z_i,z_j]) f(zi,zj)=g([zi,zj]) |
| Hadamard 哈达玛乘积 | f ( z i , z j ) = g ( z i ∗ z j ) f(z_i,z_j)=g(z_i*z_j) f(zi,zj)=g(zi∗zj) |
| Sum/Avg 求和/求平均值 | f ( z i , z j ) = g ( z i + z j ) f(z_i,z_j)=g(z_i+z_j) f(zi,zj)=g(zi+zj) |
| Distance 求距离 | f ( z i , z j ) = g ( ∥ z i − z j ∥ 2 ) f(z_i,z_j)=g(\|z_i-z_j\|_2) f(zi,zj)=g(∥zi−zj∥2) |
需要说明的是,上面提到的两种方法在针对不同的任务时各有千秋。根据2017年的一个调查(Goyal and Ferrara, 2017 survey)显示,node2vec方法在节点分类任务上表现更好,multi-hop方法在链路/关系预测任务上表现更好。随机游走方法通常效率更高。
3. Translating Embedding for Modeling Multi-relational Data——An Application of Embeddings to the Knowledge Graph
下面介绍在知识图谱上的embedding。知识图谱是一系列有关联的实体。知识图谱的不完备性会极大地影响知识系统的运行效率。这样一来,知识图谱完备性的第一个任务就是关系预测(Link Prediction)。
Link Prediction
目的——我们需要一个从KG中的本地和全球连接模式中学习的链路预测模型,同时考虑到不同类型的实体和关系。
下游任务——relation predictions are performed by using the learned patterns to generalize observed relationships between an entity of interest and all the other entities.
Translating Embeddings
在TransE方法中,实体及其之间的关系通过三元组来表示:
h ( h e a d e n t i t y ) , l ( r e l a t i o n ) , t ( t a i l r n t i t y ) = > ( h , l , t ) h(head entity), l(relation), t(tail rntity) => (h,l,t) h(headentity),l(relation),t(tailrntity)=>(h,l,t)
首先,实体被embedded到实体向量空间 R k R^k Rk,这个过程类似之前的Node embedding的方法。在此基础上,关系通过translations来表示——如果 ( h , l , t ) (h,l,t) (h,l,t)是已知的三元组,则 h + l ≈ t h+l \approx t h+l≈t;否则 h + l ≠ t h+l \not= t h+l=t。

Translating Embeddings算法如下:
4. Embedding entire graph

将整个图进行embedded的任务有:区分有毒分子和无毒分子/异常图识别……。
(1)方法一——simple idea
z G = ∑ v ∈ G z v z_G=\sum_{v \in G} z_v zG=v∈G∑zv
Duvenaud et al., 2016曾经采用这种方法将不同的分子进行分类。
(2)方法二——“virtual node”
引入“虚拟节点”来表示子图,图中的其它节点均与该节点相连,然后在其上执行标准的图嵌入算法。
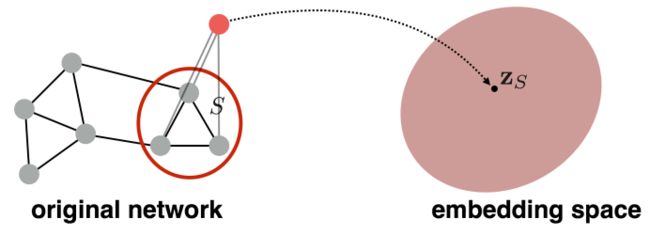
该方法由Li et al., 2016提出,作为一种通用的子图嵌入技术。
(3)方法三——anonymous walk