《剑指Offer》Java版中篇（面试题23-44，多种解题思路）

     《剑指Offer》第23道题-第44题的Java版的解题思路和代码示例。Github的地址为：https://github.com/hzka/Sword2OfferJava
（*）面试题27:二叉树的镜像
问题描述：
       操作给定的二叉树，将其变换为源二叉树的镜像。
解题思路一：
       根据源二叉树和镜像二叉树的对应关系，可以根据源二叉树的DRL得到镜像二叉树的先序遍历；根据源二叉树的RDL得到镜像二叉树的中序遍历，根据先序和中序遍历可得到唯一的重建后的二叉树。参考链接（面试题7：根据先序中序重建二叉树）：https://blog.csdn.net/weixin_38244174/article/details/89430151 但题目要求是在源二叉树进行转换，新建二叉树存在一些问题。故而舍弃掉。 Mine
解题思路二：
    （较优）根据源二叉树和镜像二叉树的对应关系，先序或者后序遍历，递归执行交换左右子树操作。直到root==null为止。递归递归递归啊！！！！考虑到直接交换左右子树，应该很简单的啊。
代码示例二：

    public void Mirror(TreeNode root) {
        if(root==null){
            return;
        }
        TreeNode tmp =  root.left;
        root.left = root.right;
        root.right = tmp;
        Mirror(root.left);
        Mirror(root.right);
}

面试题28:对称的二叉树
题目描述
     请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。
解题思路一：
       第一步：将二叉树克隆一份出来，复制左子树，复制右子树，复制根节点等等；第二步：得到二叉树的镜像，思路参考面试题27二叉树的镜像；第三步，比较两棵二叉树是否相同。思路参考面试题26树的子结构.Mine
代码示例一：

 static boolean isSymmetrical(TreeNode pRoot) {
        TreeNode pRoot_Mirror = pRoot;
        TreeNode pRoot_origin = CloneTree(pRoot);
        GetMirror(pRoot_Mirror);
        return getSimilarity(pRoot_origin, pRoot_Mirror);
    }
    private static TreeNode CloneTree(TreeNode pRoot) {
        TreeNode node = null;
        if (pRoot == null) return null;
        node = new TreeNode(pRoot.val);
        node.left = CloneTree(pRoot.left);
        node.right = CloneTree(pRoot.right);
        return node;
    }
    private static boolean getSimilarity(TreeNode pRoot, TreeNode pRoot_mirror) {
        if (pRoot != null && pRoot_mirror == null) return false;
        if (pRoot == null && pRoot_mirror != null) return false;
        if (pRoot == null && pRoot_mirror == null) return true;
        if (pRoot.val != pRoot_mirror.val) return false;
        return getSimilarity(pRoot.left, pRoot_mirror.left) && getSimilarity(pRoot.right, pRoot_mirror.right);
    }
    private static void GetMirror(TreeNode pRoot_mirror) {
        if (pRoot_mirror == null) return;
        TreeNode treeNode = pRoot_mirror.left;
        pRoot_mirror.left = pRoot_mirror.right;
        pRoot_mirror.right = treeNode;
        GetMirror(pRoot_mirror.left);
        GetMirror(pRoot_mirror.right);
}

解题思路二：
     （较优）分析之间的依赖关系，包括：首先根节点以及其左右子树，左子树的左子树和右子树的右子树相同，左子树的右子树和右子树的左子树相同即可，采用递归非递归也可，采用栈或队列存取各级子树根节点，其实我可以想到。
代码示例二：

    boolean isSymmetrical(TreeNode pRoot) {
        if(pRoot ==null)  return true;
        return compareWith(pRoot.left,pRoot.right);
    }
    private static boolean compareWith(TreeNode left, TreeNode right) {
        if(left ==null && right ==null) return true;
        if(left!=null && right!=null)
            return left.val == right.val && compareWith(left.left,right.right) 
                    && compareWith(left.right,right.left);
        return false;
}

面试题29:顺时针打印矩阵
题目描述
       输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵：1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
解题思路一：
       首先承认自己代码比较冗余，但思路应该没问题，写了一两个小时。使用一个优先级确保顺时针的遍历顺序。有一个标志矩阵数组，用来存储该节点访问与否，递归的参数包括了当前矩阵、当前行、当前列、标志数组以及优先级。越界判断很重要，优先级是变化的，根据优先级来改变访问顺序。访问顺序按照顺时针进行。Mine
代码示例一：

    private static ArrayList arrayList = new ArrayList();
    private static int priority_judge = 0;
    public static ArrayList printMatrix(int[][] matrix) {
        if (matrix.length == 0 && matrix[0].length == 0) return null;
        boolean[][] matrix_check = new boolean[matrix.length][matrix[0].length];
        traversing(matrix, 0, 0, matrix_check, priority_judge);
        return arrayList;
    }
    private static void traversing(int[][] matrix, int row, int column, boolean[][] matrix_check, int priority_judge) {
        arrayList.add(matrix[row][column]);
        matrix_check[row][column] = true;
        boolean isValid = false;
        switch (priority_judge) {
            case 0:
                if (column >= 0 && column < matrix[0].length - 1 && !matrix_check[row][column + 1]) {
                    //优先级为0,向右走。
                    traversing(matrix, row, column + 1, matrix_check, 0);
                }
                if (0 <= row && row < matrix.length - 1 && !matrix_check[row + 1][column]) {
                    //优先级为1,向下走。
                    traversing(matrix, row + 1, column, matrix_check, 1);
                }
                if (column - 1 >= 0 && !matrix_check[row][column - 1]) {
                    //优先级为2,向左走。
                    traversing(matrix, row, column - 1, matrix_check, 2);
                }
                if (row - 1 >= 0 && !matrix_check[row - 1][column]) {
                    //优先级为3,向上走。
                    traversing(matrix, row - 1, column, matrix_check, 3);
                }
                break;
            case 1:
                if (0 <= row && row < matrix.length - 1 && !matrix_check[row + 1][column]) {
                    //优先级为1,向下走。
                    traversing(matrix, row + 1, column, matrix_check, 1);
                }
                if (column - 1 >= 0 && !matrix_check[row][column - 1]) {
                    //优先级为2,向左走。
                    traversing(matrix, row, column - 1, matrix_check, 2);
                }
                if (row - 1 >= 0 && !matrix_check[row - 1][column]) {
                    //优先级为3,向上走。
                    traversing(matrix, row - 1, column, matrix_check, 3);
                }
                if (column >= 0 && column < matrix[0].length - 1 && !matrix_check[row][column + 1]) {
                    //优先级为0,向右走。
                    traversing(matrix, row, column + 1, matrix_check, 0);
                }
                break;
            case 2:
                if (column - 1 >= 0 && !matrix_check[row][column - 1]) {
                    //优先级为2,向左走。
                    traversing(matrix, row, column - 1, matrix_check, 2);
                }
                if (row - 1 >= 0 && !matrix_check[row - 1][column]) {
                    //优先级为3,向上走。
                    traversing(matrix, row - 1, column, matrix_check, 3);
                }
                if (column >= 0 && column < matrix[0].length - 1 && !matrix_check[row][column + 1]) {
                    //优先级为0,向右走。
                    traversing(matrix, row, column + 1, matrix_check, 0);
                }
                if (0 <= row && row < matrix.length - 1 && !matrix_check[row + 1][column]) {
                    //优先级为1,向下走。
                    traversing(matrix, row + 1, column, matrix_check, 1);
                }
                break;
            case 3:
                if (row - 1 >= 0 && !matrix_check[row - 1][column]) {
                    //优先级为3,向上走。
                    traversing(matrix, row - 1, column, matrix_check, 3);
                }
                if (column >= 0 && column < matrix[0].length - 1 && !matrix_check[row][column + 1]) {
                    //优先级为0,向右走。
                    traversing(matrix, row, column + 1, matrix_check, 0);
                }
                if (0 <= row && row < matrix.length - 1 && !matrix_check[row + 1][column]) {
                    //优先级为1,向下走。
                    traversing(matrix, row + 1, column, matrix_check, 1);
                }
                if (column - 1 >= 0 && !matrix_check[row][column - 1]) {
                    //优先级为2,向左走。
                    traversing(matrix, row, column - 1, matrix_check, 2);
                }
                break;
        }
        return;
    }

解题思路二：
    （较优）找规律问题，先找到转的圈数(Math.min(n,m)-1)/2+1。再分别从左向右打印；从上往下打印；判断是否会重复打印(从右向左的每行数据),首先保证右边再保证左边；判断是否会重复打印(从下往上的每一列数据),首先保证下边比上边大，再保证不要往上走越界了。接着循环。最后返回结果。
代码示例二：

   public static ArrayList printMatrix(int [][] array) {
        ArrayList result = new ArrayList ();
        if(array.length==0) return result;
        int n = array.length,m = array[0].length;//行数和列数
        if(m==0) return result;
        int layers = (Math.min(n,m)-1)/2+1;//圈数
        for(int i=0;i=i)&&(n-i-1!=i);k--)
                result.add(array[n-i-1][k]);
            //判断是否会重复打印(从下往上的每一列数据),首先保证下边比上边大，再保证不要往上走越界了，
            for(int j=n-i-2;(j>i)&&(m-i-1!=i);j--)
                result.add(array[j][i]);
        }
        return result;
}

面试题30:包含min函数的栈
题目描述：
       定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。 
算法思路一：
     （较优）确认过眼神，是一道用空间换时间的题。建立两个堆栈，一个stack用来存储元素，一个min_stack用来存储每一次操作的最小元素。在push函数中先进行判断，得到最小值，进行压栈。 在pop函数中进行弹栈。Stack和min_stack都要弹栈，然后使用peek去更新min_stack当中的最小值。Mine
代码示例一：

    private Stack stack = new Stack();
    private Stack min_stack = new Stack();
    private int min = Integer.MAX_VALUE;
    public void push(int node) {
        if (node <= min){
            min = node;
        }
        min_stack.push(min);
        stack.push(node);
    }
    //弹栈的时候有可能最小值就弹出去了。
    public void pop() {
        min_stack.pop();
        min = min_stack.peek();
        stack.pop();
    }
    public int top() {
        return stack.peek();
    }
    public int min() {
        return min;
    }    

算法思路二：
    原理一致，主要是对它的扩容感兴趣。
代码示例二：

   private int size;
    private int min = Integer.MAX_VALUE;
    private Stack minStack = new Stack();
    private Integer[] elements = new Integer[10];
    public void push(int node) {
        ensureCapacity(size+1);
        elements[size++] = node;
        if(node <= min){
            minStack.push(node);
            min = minStack.peek();
        }else{
            minStack.push(min);
        }
    }
    private void ensureCapacity(int size) {
        // TODO Auto-generated method stub
        int len = elements.length;
        if(size > len){
            int newLen = (len*3)/2+1; //每次扩容方式
            elements = Arrays.copyOf(elements, newLen);
        }
    }
    public void pop() {
        Integer top = top();
        if(top != null){
            elements[size-1] = (Integer) null;
        }
        size--;
        minStack.pop();
        min = minStack.peek();
        //    System.out.println(min+"");
    }
    public int top() {
        if(!empty()){
            if(size-1>=0)
                return elements[size-1];
        }
        return (Integer) null;
    }
    public boolean empty(){
        return size == 0;
    }
    public int min() {
        return min;
    }

面试题31:栈的压入、弹出序列
题目描述：
       输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）
算法思路一：（较优）
    （1）假设两个数组的长度都为零，则返回true;
    （2）假设两个数组的长度不相等，则返回false;
    （3）设定两个计数器，分别记录pushA数组和popA数组的下标位置，建立堆栈，先入栈再出栈：将pushA第一个元素push进栈，紧接着比较popA中的第一个元素，若peek出来的相等，弹栈，下标+1，while循环；若不等，则i++，压栈下一个元素，每一次都进行比较。注意当栈的大小大于等于1时，才能peek不会报错。结束条件是如果i==pushA.length&&j==popA.length，返回true;如果是i走完j没有走完亦或者是j走完i没有走完，返回false。
代码示例一：

public class Main {
    static Stack my_stack = new Stack();
    public static boolean IsPopOrder(int[] pushA, int[] popA) {
        if (pushA.length != popA.length) return false;
        if (pushA.length == popA.length && pushA.length == 0) return true;
        int i = 0, j = 0;
        while (i < pushA.length && j < popA.length) {
            my_stack.push(pushA[i]);
            while (my_stack.size() >= 1 && my_stack.peek() == popA[j]) {
                my_stack.pop();
                j++;
            }
            i++;
            if (i == pushA.length && j != popA.length) return false;
            if (i != pushA.length && j == popA.length)  return false;
        }
        return true;
    }
}

算法思路2：
       别人的结束条件比我写得好，其他一样。
代码示例2：

public class Solution {
    public boolean IsPopOrder(int [] pushA,int [] popA) {
        if(pushA.length == 0 || popA.length == 0)
            return false;
        Stack s = new Stack();
        //用于标识弹出序列的位置
        int popIndex = 0;
        for(int i = 0; i< pushA.length;i++){
            s.push(pushA[i]);
            //如果栈不为空，且栈顶元素等于弹出序列
            while(!s.empty() &&s.peek() == popA[popIndex]){
                //出栈
                s.pop();
                //弹出序列向后一位
                popIndex++;
            }
        }
        return s.empty();
    }
}

面试题32:从上往下打印二叉树
题目描述：
       从上往下打印出二叉树的每个节点，同层节点从左至右打印。
算法思路：
       说白了就是层次遍历，本科的时候老师就教过我们使用一个队列来暂存树中的节点。LinkedList(实现了queue,deque接口,List接口)实现队列，可以使用它去做这个Queue。（1）先在队列中添加root节点，判断当前队列是不是为空，若不为空，移除该节点并将该节点的值放入Arraylist中，随后将该节点的左孩子节点和右孩子节点添加进队列中；（2）若当前队列不为空，则继续移除队列头部的节点，并将其孩子节点放入队列中，直至队列空为止。最后返回Arraylist。注意两点：（1）在循环遍历时需要判断孩子节点是否为空，不为空再将其添加队列。一般来说，队列会添加空元素，添加之后报错。（2）刚开始，若root节点为空，则返回一个空数组，而不是一个null。
代码示例：

    public ArrayList PrintFromTopToBottom(TreeNode root) {
        ArrayList arraylist = new ArrayList();
        if(root == null){
            return arraylist;
        }
        Queue queue = new LinkedList();
        queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode nowParent = queue.remove();
            arraylist.add(nowParent.val);
            if (nowParent.left != null) {
                queue.add(nowParent.left);
            }
            if (nowParent.right != null) {
                queue.add(nowParent.right);
            }
        }
        return arraylist;
}

面试题33:二叉搜索树的后序遍历序列
题目描述
        输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
算法思路一：
        想发现后序遍历数组中的规律，很遗憾没有找到。但想到了1.二叉搜索树的先序遍历是一个有序递增的数组；2.根据先序和后序能够唯一的重建二叉树，如果能建成，则说明后序遍历结果没问题；如果建不成，则说明后序遍历结果有问题。参考了面试题6：重建二叉树。参考链接：https://blog.csdn.net/weixin_38244174/article/details/89430151  mine
代码示例一：

public class Solution {
    public boolean VerifySquenceOfBST(int [] sequence) {
        if(sequence.length == 0) return false;
        int [] in = Arrays.copyOf(sequence,sequence.length);
        Arrays.sort(sequence);
        try {
            reConstructBinaryTree(sequence, in);
            return true;
        }catch (Exception e){
            return false;
        }
    }
    public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
        if (pre == null || in == null || pre.length != in.length) {
            return null;
        }
        return construct(pre, 0, pre.length - 1, in, 0, in.length - 1);
    }
    private TreeNode construct(int[] pre, int pre_start, int pre_end, int[] in, int in_start, int in_end) {
        if (pre_start > pre_end) return null;
        //取前序遍历的第一个数字为根节点
        int value = pre[pre_start];
        //在中序中遍历寻找该根节点
        int index = in_start;
        while (index <= in_end && value != in[index]) {
            index++;
        }
        //判断溢出条件
        if (index > in_end) throw new RuntimeException("Invalid Input");
        TreeNode treeNode = new TreeNode(value);
        treeNode.left = construct(pre, pre_start + 1, pre_start + index - in_start, in, in_start, index - 1);
        treeNode.right = construct(pre, pre_start + index - in_start + 1, pre_end, in, index + 1, in_end);
        return treeNode;
    }
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) {
            val = x;
        }
    }
}

算法思路二：
      （较优）找住二叉查找树的特点：左子树<根<=右子树，使用分治思想。
代码示例二：

public class Solution {
    public boolean VerifySquenceOfBST(int [] sequence) {
        if(sequence.length == 0) return false;
        if(sequence.length == 1) return true;
        return judge(sequence,0,sequence.length-1);
    }
   public boolean judge(int []a,int start,int end){
       if(start>=end) return true;
       int i = start;
       while(a[i]

（*）面试题34:二叉树中和为某一值的路径
题目描述：
       输入一颗二叉树的跟节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)
算法思路：
      （1）递归先序遍历树， 把结点加入路径。（2）若该结点是叶子结点则比较当前路径和是否等于期待和。（3）弹出结点，每一轮递归返回到父结点时，当前路径也应该回退一个结点。未考虑到三点：（1）遍历至叶子节点需要返回时如何弹出动态数组中的值？解决方法：若递归过程左右子树都为null，则走到FindPath(root.right,target)，此时只需要remove掉当前动态数组中的最后一个即可。（2）在将当前动态数组存储进待返回动态数组时，一定要新建一个数组存储当前数组再Add进去。否则待返回数组所添加的当前数组是不断变化的，切记；（3）操作前，先判断root是否等于null。若等于null，直接返回即可。
代码示例：

public class Solution {
     public  ArrayList> alllist = new ArrayList>();
     public  ArrayList arraylist = new ArrayList();
     public ArrayList> FindPath(TreeNode root,int target)  {
        if (root != null) {
        arraylist.add(root.val);
        if (root.left == null && root.right == null) {
            int sum = 0;
            for (int i = 0; i < arraylist.size(); i++) {
                sum += arraylist.get(i);
            }
            if (sum == target) {
                alllist.add(new ArrayList(arraylist));
            }
        }
        FindPath(root.left, target);
        FindPath(root.right, target);
        arraylist.remove(arraylist.size() - 1);}
        return alllist;
    }
}

（**）面试题35:复杂链表的复制
题目描述
        输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点），返回结果为复制后复杂链表的head。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）
算法思路：
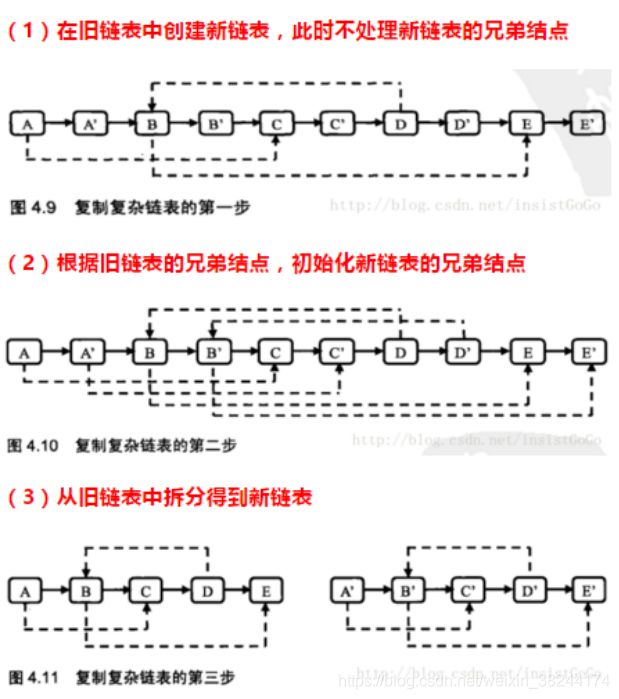
       1.遍历链表，复制每个结点，如复制结点A得到A1，将结点A1插到结点A后面；
       2.重新遍历链表，复制老结点的随机指针给新结点，如A1.random = A.random.next;
       3.拆分链表，将链表拆分为原链表和复制后的链表

                                          
代码示例：

public class Solution {
    public RandomListNode Clone(RandomListNode pHead)
       {
        if(pHead == null) return null;
        RandomListNode currentNode = pHead;
        //1.复制每一个节点，譬如复制节点A到节点A1，将节点A1插到节点A的后面,将指针指向NextNode位置，
        while(currentNode!=null){
            RandomListNode cloneNode = new RandomListNode(currentNode.label);
            RandomListNode nextNode = currentNode.next;
            currentNode.next = cloneNode;
            cloneNode.next = nextNode;
            currentNode = nextNode;
        }
        currentNode = pHead;
        //2.重新遍历链表，复制老节点的随机指针给新节点，譬如A1.random = A.random.next;
        while(currentNode!=null){
            currentNode.next.random = currentNode.random == null?null:currentNode.random.next;
            currentNode = currentNode.next.next;
        }
        //3.拆分链表，将链表拆分为原链表和复制后得链表
        currentNode = pHead;
        RandomListNode pCloneNode = pHead.next;
        while(currentNode!=null){
            RandomListNode cloneNode = currentNode.next;
            currentNode.next = cloneNode.next;
            cloneNode.next = cloneNode.next==null?null:cloneNode.next.next;
            currentNode = currentNode.next;
        }
        return pCloneNode;
    }
}

（***）面试题36:二叉搜索树与双向链表
题目描述：
       输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。
解题思路一：
      （非递归版较优） 1.核心是中序遍历的非递归算法。2.修改当前遍历节点与上一个历节点的指针指向。（1）使用堆栈暂存节点p，一直到p的左节点；（2）弹栈判断是不是第一个节点；（3）若不是第一个节点，则改变指针指向。遍历到p的right节点。
代码示例一：

    public static TreeNode Convert(TreeNode root) {
        if(root==null)  return null;
        Stack stack = new Stack();
        TreeNode p =root;
        TreeNode pre = null;//用于保存中序遍历的上一节点
        boolean isFirst = true;
        while (p!=null || !stack.isEmpty()){
            while (p!=null){
                stack.push(p);
                p = p.left;
            }
            p = stack.pop();
            if(isFirst){
                root = p;
                pre = root;
                isFirst = false;
            }else{
                pre.right = p;
                p.left = pre;
                pre = p;
            }
            p = p.right;
        }
       return root;
}

算法思路二：
      （递归版没搞懂）1.将左子树构造成双链表，并返回链表头节点。2.定位至左子树双链表最后一个节点。3.如果左子树链表不为空的话，将当前root追加到左子树链表。4.将右子树构造成双链表，并返回链表头节点。5.如果右子树链表不为空的话，将该链表追加到root节点之后。6.根据左子树链表是否为空确定返回的节点。
代码思路二：

    public static TreeNode Convert(TreeNode root) {
        if(root == null)  return null;
        if(root.left == null && root.right == null)  return root;
//        1.将左子树构造成双链表，并返回链表头节点。
        TreeNode left = Convert(root.left);
        TreeNode p = left;
//        2.定位至左子树双链表最后一个节点。
        while (p!=null && p.right!=null){
            p = p.right;
        }
//       3.如果左子树链表不为空的话，将当前root追加到左子树链表。
        if(left!=null){
            p.right = root;
            root.left = p;
        }
//       4.将右子树构造成双链表，并返回链表头节点。
        TreeNode right = Convert(root.right);
//       5.如果右子树链表不为空的话，将该链表追加到root节点之后。
       if(right!=null){
           right.left = root;
           root.right = right;
       }
       return left!=null?left:root;
    }

（**）面试题37:序列化二叉树
题目描述：
       请实现两个函数，分别用来序列化和反序列化二叉树。
解题思路：
     （1）序列化较为简单，递归先序遍历，假设node节点为null，则返回一个添加#,后的字符串；否则返回一个root.val+”,”的字符串；（2）反序列化后的二叉树只需要先序遍历即可确定唯一二叉树。（根据面试题7，重建二叉树我们知道：先序+中序或者中序+后序可唯一确定一棵二叉树）。先对字符串分割成数组，再判断分割后的字符串是否等于null，若等于null，则直接返回null即可。假设不为空，新建节点，递归重建即可。
代码示例：

public class Solution {
    int index = -1;
     String Serialize(TreeNode root) {
       StringBuilder sb = new StringBuilder();
       if(root == null) return sb.append("#,").toString();
       sb.append(root.val+",");
       sb.append(Serialize(root.left));
       sb.append(Serialize(root.right));
       return sb.toString();
    }
     TreeNode Deserialize(String str) {
        index++;
        String[] splits = str.split(",");
        TreeNode node = null;
        if(!splits[index].equals("#")){
            node = new TreeNode(Integer.valueOf(splits[index]));
            node.left = Deserialize(str);
            node.right = Deserialize(str);
        }
        return node;
    }
}

（***）面试题38:字符串的排列
题目描述：
       输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。
解题思路：

                                        
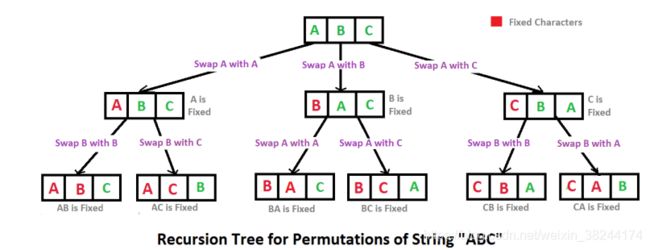
       对于无重复值的情况
       固定第一个字符，递归取得首位后面的各种字符串组合；再把第一个字符与后面每一个字符交换，并同样递归获得首位后面的字符串组合； *递归的出口，就是只剩一个字符的时候，递归的循环过程，就是从每个子串的第二个字符开始依次与第一个字符交换，然后继续处理子串。
       假如有重复值呢？
       由于全排列就是从第一个数字起，每个数分别与它后面的数字交换，我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这两个数就不交换了。例如abb，第一个数与后面两个数交换得bab，bba。然后abb中第二个数和第三个数相同，就不用交换了。但是对bab，第二个数和第三个数不 同，则需要交换，得到bba。 由于这里的bba和开始第一个数与第三个数交换的结果相同了，因此这个方法不行。
       换种思维，对abb，第一个数a与第二个数b交换得到bab，然后考虑第一个数与第三个数交换，此时由于第三个数等于第二个数，所以第一个数就不再用与第三个数交换了。再考虑bab，它的第二个数与第三个数交换可以解决bba。此时全排列生成完毕！
代码示例：

public class Main {
    public static void main(String[] args) {
        Permutation("ojbk");
    }
    public static ArrayList Permutation(String str) {
        ArrayList lists = new ArrayList();
        if (str != null && str.length() > 0) {
            PermutationHelper(str.toCharArray(), 0, lists);
            //按照字典序排序
            Collections.sort(lists);
        }
        return lists;
    }
    private static void PermutationHelper(char[] charArray, int i, ArrayList lists) {
        if (i == charArray.length - 1) {
            String val = String.valueOf(charArray);
            if(!lists.contains(val)){
                lists.add(val);
            }
        }else{
             //这一段就是回溯法，这里以"abc"为例
            //递归的思想与栈的入栈和出栈是一样的,某一个状态遇到return结束了之后，会回到被调用的地方继续执行
            //1.第一次进到这里是ch=['a','b','c'],list=[],i=0，我称为 状态A ，即初始状态
            //那么j=0，swap(ch,0,0)，就是['a','b','c']，进入递归，自己调自己，只是i为1，交换(0,0)位置之后的状态我称为 状态B
            //i不等于2，来到这里，j=1，执行第一个swap(ch,1,1)，这个状态我称为 状态C1 ,再进入fun函数，此时标记为T1，i为2，那么这时就进入上一个if，将"abc"放进list中
            /-------》此时结果集为["abc"]
            //2.执行完list.add之后，遇到return，回退到T1处，接下来执行第二个swap(ch,1,1)，状态C1又恢复为状态B
            //恢复完之后，继续执行for循环，此时j=2,那么swap(ch,1,2),得到"acb"，这个状态我称为C2,然后执行fun，此时标记为T2,发现i+1=2,所以也被添加进结果集，此时return回退到T2处往下执行
            /-------》此时结果集为["abc","acb"]
            //然后执行第二个swap(ch,1,2)，状态C2回归状态B,然后状态B的for循环退出回到状态A

            //             a|b|c(状态A)
            //               |
            //               |swap(0,0)
            //               |
            //             a|b|c(状态B)
            //             /  \
            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
            //           /      \
            //         a|b|c   a|c|b

            //3.回到状态A之后，继续for循环，j=1,即swap(ch,0,1)，即"bac",这个状态可以再次叫做状态A,下面的步骤同上
            /-------》此时结果集为["abc","acb","bac","bca"]

            //             a|b|c(状态A)
            //               |
            //               |swap(0,1)
            //               |
            //             b|a|c(状态B)
            //             /  \
            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
            //           /      \
            //         b|a|c   b|c|a

            //4.再继续for循环，j=2,即swap(ch,0,2)，即"cab",这个状态可以再次叫做状态A，下面的步骤同上
            /-------》此时结果集为["abc","acb","bac","bca","cab","cba"]

            //             a|b|c(状态A)
            //               |
            //               |swap(0,2)
            //               |
            //             c|b|a(状态B)
            //             /  \
            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
            //           /      \
            //         c|b|a   c|a|b

            //5.最后退出for循环，结束。
            for(int j = i;j

面试题39:数组中出现次数超过一半的数字
题目描述：
       数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。
解题思路一：
     （1）先判定数组长度为零和数组长度为一的情况；（2）Arrays.sort快速排序，获得排序后的数组。（3）从array[1]开始遍历判断，假设当前数字的和前一个数字相等，则计数器++，如果计数器+1大于数组长度的一半，则返回array[i]即可；否则则将计数器置零，若未提前返回，则最后返回零。
代码示例一：

public class Solution {
    public int MoreThanHalfNum_Solution(int [] array) {
        Arrays.sort(array);
        if(array.length == 0) return 0;
        if(array.length == 1) return array[0];
        int counting  = 0;
        for(int i = 1;i array.length/2) 
                    return array[i];
            }else{
                counting = 0;
            }
        }
        return 0;
    }
}

解题思路二：
       采用阵地攻守的思想：第一个数字作为第一个士兵，守阵地；count = 1；遇到相同元素，count++;遇到不相同元素，即为敌人，同归于尽,count--；当遇到count为0的情况，又以新的i值作为守阵地的士兵，继续下去，到最后还留在阵地上的士兵，有可能是主元素。再加一次循环，记录这个士兵的个数看是否大于数组一半即可。
代码示例二：

public class Solution {
    public int MoreThanHalfNum_Solution(int [] array) {
        if(array.length == 0) return 0;
        if(array.length == 1) return array[0];
        int counting = 1;
        int nownumber = array[0];
        for(int i  = 1;iarray.length/2)  return nownumber;
         }
        return 0;
    }
}

面试题40:最小的K个数
题目描述：
       输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。
算法思路一：
       先使用快排Arrays.sort()这一个API，再新建动态数组，将前k个最小值添加进去。需要注意的是：对于不合法输入的判断。
代码示例一：

    public ArrayList GetLeastNumbers_Solution(int [] input, int k) {
        Arrays.sort(input);
        ArrayList arraylist = new ArrayList();
        if(k>input.length) return arraylist;
        for(int i = 0;i < k;i++){
            arraylist.add(input[i]);
        }
        return arraylist;
}

算法思路二：
     （较优）用最大堆保存这k个数，每次只和堆顶比，如果比堆顶小，删除堆顶，新数入堆。最大堆的实现使用优先队列。Queue maxHeap = new PriorityQueue(k, Collections.reverseOrder());（在方法调用返回一个比较器，它强行上实现Comparable接口的对象的集合的自然顺序相反）
代码示例二：

public class Solution {
    public ArrayList GetLeastNumbers_Solution(int [] input, int k) {
       ArrayList result = new ArrayList();
       int length = input.length;
       if(k>length||k==0||input ==null){
           return result;
       }
       //从大到小的n为优先数组，每次返回最大的值。
        Queue maxHeap = new PriorityQueue(k, Collections.reverseOrder());
        for(int i = 0;i

面试题41：数据流中的中位数
题目描述：
        如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。
算法思路一：
        Insert()方法中使用动态数组存储数据流，GetMedian()方法先将动态数组存储到int类型的数组中，再使用快速排序，最后看动态数组的长度是否为偶数，若为偶数，返回平均值，若为奇数，则返回中间值即可。取巧了Arrays.sort()。
代码示例一：

import java.util.*;
public class Solution {
    ArrayList arraylist = new ArrayList();
    public void Insert(Integer num) {
        arraylist.add((double)num);
    }
    public Double GetMedian() {
        int length = arraylist.size();
        double []allnum = new double[length];
        for(int i =0;i

算法思路二：
       Java的PriorityQueue 是从JDK1.5开始提供的新的数据结构接口，默认内部是自然排序，结果为小顶堆，也可以自定义排序器，比如下面反转比较，完成大顶堆。为了保证插入新数据和取中位数的时间效率都高效，这里使用大顶堆+小顶堆的容器，并且满足：1、两个堆中的数据数目差不能超过1，这样可以使中位数只会出现在两个堆的交接处；2、大顶堆的所有数据都小于小顶堆，这样就满足了排序要求。（当数据总数为偶数时，新加入的元素，应当进入小根堆，经大根堆筛选之后进入小根堆；当数据总数为奇数时，新加入的元素，应当进入大根堆，经小根堆筛选之后进入大根堆。）
代码示例二：

import java.util.*;
public class Solution {
    private int count = 0;
    private PriorityQueue minHeap = new PriorityQueue();//小根堆
    private  PriorityQueue maxHeap = new PriorityQueue(15, Collections.reverseOrder());

    public  void Insert(Integer num) {
        if (count % 2 == 0) {//当数据总数为偶数时，新加入的元素，应当进入小根堆
            //（注意不是直接进入小根堆，而是经大根堆筛选后取大根堆中最大元素进入小根堆）
            //1.新加入的元素先入到大根堆，由大根堆筛选出堆中最大的元素
            maxHeap.add(num);
            int filteredMaxNum = maxHeap.remove();
            //2.筛选后的【大根堆中的最大元素】进入小根堆
            minHeap.add(filteredMaxNum);
        }else{//当数据总数为奇数时，新加入的元素，应当进入大根堆
            //（注意不是直接进入大根堆，而是经小根堆筛选后取小根堆中最大元素进入大根堆）
            //1.新加入的元素先入到小根堆，由小根堆筛选出堆中最小的元素
            minHeap.add(num);
            int filteredMinNum = minHeap.remove();
            maxHeap.add(filteredMinNum);
        }
        count++;
    }
    public Double GetMedian() {
        if(count%2 == 0){
            return new Double(minHeap.peek()+maxHeap.peek())/2;
        }else{
            return new Double(minHeap.peek());
        }
    }
}

面试题42：连续整数的最大和
题目描述一：
        若该数左边的序列的和为正数，则将其加进去，否则将当前数作为开始元素。考虑到输入全为负数的情况。固定两个下标，一个记录开始位置，一个记录结束位置，若之和小于0，则break掉。若开始位置到结束位置的和大于MAX_VALUE的值，则更新MAX_VALUE。
代码示例一：

    public static int FindGreatestSumOfSubArray(int[] array) {
        int MAX_VALUE = 0;
        for (int i = 0; i < array.length; i++) {
            if (array[i] < 0) continue;
            int nownum = 0;
            for (int j = i; j < array.length; j++) {
                //试探着走。
                nownum += array[j];
                if (nownum < 0) break;
                if (nownum > MAX_VALUE) {
                    MAX_VALUE = nownum;
                }
            }
        }
        if(MAX_VALUE == 0){
            MAX_VALUE = array[0];
            for (int i = 0; i < array.length; i++) {
                 MAX_VALUE  = MAX_VALUE

算法思路二：
    （较优）算法时间复杂度O（n），用total记录累计值，maxSum记录和最大，于一个数A，若是A的左边累计数非负，那么加上A能使得值不小于A，认为累计值对整体和是有贡献的。如果前几项累计值负数，则认为有害于总和，total记录当前值。此时，若和大于maxSum 则用maxSum记录下来。别人是一遍遍历即可。
代码示例二：

    public static int FindGreatestSumOfSubArray(int[] array) {
        if (array.length == 0) return 0;
        if (array.length == 1) return array[0];
        int total = array[0], maxSum = array[0];
        for (int i = 1; i < array.length; i++) {
            if (total >= 0)
                total += array[i];
            else
                total = array[i];
            if (total > maxSum)
                maxSum = total;
        }
        return maxSum;
}  

算法思路三：
      使用动态规划。
      F（i）：以array[i]为末尾元素的子数组的和的最大值，子数组的元素的相对位置不变
      F（i）=max（F（i-1）+array[i] ， array[i]）
      res：所有子数组的和的最大值res=max（res，F（i））
      如数组[6, -3, -2, 7, -15, 1, 2, 2]
      初始状态：
      i=0：F（0）=6  res=6
      i=1：F（1）=max（F（0）-3，-3）=max（6-3，3）=3；res=max（F（1），res）=max（3，6）=6
      i=2：F（2）=max（F（1）-2，-2）=max（3-2，-2）=1；res=max（F（2），res）=max（1，6）=6
      i=3：F（3）=max（F（2）+7，7）=max（1+7，7）=8；res=max（F（2），res）=max（8，6）=8
      i=4：F（4）=max（F（3）-15，-15）=max（8-15，-15）=-7；res=max（F（4），res）=max（-7，8）=8
     以此类推 ，最终res的值为8。
代码示例三：

public class Solution {
    public int FindGreatestSumOfSubArray(int[] array)  {
        int res = array[0];//记录当前所有子数组的和的最大值
        int max = array[0];//包含array[i]的连续数组最大值
        for(int i = 1;i

面试题43：整数中1出现的次数（从1到n整数中1出现的次数）
题目描述
       求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。
算法思路一：
       暴力破解，设定计数器，然后判断每个数的每一位是否是1，若为，则计数器+1，否则，不加。循环条件是：
 while (nownumber > 0) { int remainder = nownumber % 10;  nownumber = nownumber / 10; }
代码示例一：

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {
        if (n <= 0) return 0;
        int counting = 0;
        for (int i = 1; i <= n; i++) {
            int nownumber = i;
            while (nownumber > 0) {
                int remainder = nownumber % 10;
                if (remainder == 1) {
                    counting++;
                }
                nownumber = nownumber / 10;
            }
        }
        return counting;
    }
}

算法思路二：
       像类似这样的问题，我们可以通过归纳总结来获取相关的东西。首先可以先分类：
      个位
       我们知道在个位数上，1会每隔10出现一次，例如1、11、21等等，我们发现以10为一个阶梯的话，每一个完整的阶梯里面都有一个1，例如数字22，按照10为间隔来分三个阶梯，在完整阶梯0-9，10-19之中都有一个1，但是19之后有一个不完整的阶梯，我们需要去判断这个阶梯中会不会出现1，易推断知，如果最后这个露出来的部分小于1，则不可能出现1（这个归纳换做其它数字也成立）。我们可以归纳个位上1出现的个数为：n/10 * 1+(n%10!=0 ? 1 : 0)
      十位
      现在说十位数，十位数上出现1的情况应该是10-19，依然沿用分析个位数时候的阶梯理论，我们知道10-19这组数，每隔100出现一次，这次我们的阶梯是100，例如数字317，分析有阶梯0-99，100-199，200-299三段完整阶梯，每一段阶梯里面都会出现10次1（从10-19），最后分析露出来的那段不完整的阶梯。我们考虑如果露出来的数大于19，那么直接算10个1就行了，因为10-19肯定会出现；如果小于10，那么肯定不会出现十位数的1；如果在10-19之间的，我们计算结果应该是k - 10 + 1。例如我们分析300-317，17个数字，1出现的个数应该是17-10+1=8个。那么现在可以归纳：十位上1出现的个数为：设k = n % 100，即为不完整阶梯段的数字；归纳式为：(n / 100) * 10 + (if(k > 19) 10 else if(k < 10) 0 else k - 10 + 1)
        百位
        现在说百位1，我们知道在百位，100-199都会出现百位1，一共出现100次，阶梯间隔为1000，100-199这组数，每隔1000就会出现一次。这次假设我们的数为2139。跟上述思想一致，先算阶梯数 * 完整阶梯中1在百位出现的个数，即n/1000 * 100得到前两个阶梯中1的个数，那么再算漏出来的部分139，沿用上述思想，不完整阶梯数k199，得到100个百位1，100<=k<=199则得到k - 100 + 1个百位1。
那么继续归纳百位上出现1的个数：设k = n % 1000。归纳式为：(n / 1000) * 100 + (if(k >199) 100 else if(k < 100) 0 else k - 100 + 1)
       后面的依次类推....
       再次回顾个位
       我们把个位数上算1的个数的式子也纳入归纳式中：
       k = n % 10
      个位数上1的个数为：n / 10 * 1 + (if(k > 1) 1 else if(k < 1) 0 else k - 1 + 1)
完美！归纳式看起来已经很规整了。 来一个更抽象的归纳，设i为计算1所在的位数，i=1表示计算个位数的1的个数，10表示计算        十位数的1的个数等等。
      k = n % (i * 10)    count(i) = (n / (i * 10)) * i + (if(k > i * 2 - 1) i else if(k < i) 0 else k - i + 1)
      好了，这样从10到10的n次方的归纳就完成了。
      sum1 = sum(count(i))，i = Math.pow(10, j), 0<=j<=log10(n)
      但是有一个地方值得我们注意的，就是代码的简洁性来看，有多个ifelse不太好，能不能进一步简化呢？ 我们可以把后半段简化成这样，我们不去计算i * 2 - 1了，我们只需保证k - i + 1在[0, i]区间内就行了，最后后半段可以写成这样min(max((n mod (i*10))−i+1,0),i)
代码示例二：

   public static int NumberOf1Between1AndN_Solution(int n) {
        if(n <= 0)
            return 0;
        int count = 0;
        for(long i = 1; i <= n; i *= 10){
            long diviver = i * 10;
            count += (n / diviver) * i + Math.min(Math.max(n % diviver - i + 1, 0), i);
        }
        return count;
}

面试题45：把数组排成最小的数
题目描述：
       输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。
算法思路一：
     （1）假设数组长度为0，则返回空的String字符串；若为1，则返回第一个数字转字符串的结果；（2）计算数组中最大的数字的长度，将其他字符串拼接成这么长的字符串。（3）然后使用冒泡排序进行排序，将较小的数字放于前面，较大的放在后面；（4）依次拼接字符串。譬如：3、32、321，先拼成333、323、321.再经冒泡排序成了321、323、333。而其对应的数组为321、32、3。拼接出来就是321323。
代码示例一：

public class Solution {
    public String PrintMinNumber(int [] numbers) {
        if(numbers.length == 0) return String.valueOf(new StringBuilder());
        if(numbers.length == 1) return String.valueOf(numbers[0]);
        int MAX = Integer.MIN_VALUE;
        for (int i = 0; i < numbers.length; i++) {
            if (numbers[i] > Integer.MIN_VALUE) {
                MAX = numbers[i];
            }
        }
        int MAX_length = String.valueOf(MAX).length();
        for (int i = 0; i < numbers.length - 1; i++) {
            for (int j = i + 1; j < numbers.length; j++) {
                //填充数字
                int length_i = MAX_length - String.valueOf(numbers[i]).length();
                int length_j = MAX_length - String.valueOf(numbers[j]).length();
                if (dealNum(numbers[i],length_i) > dealNum(numbers[j],length_j)) {
                    int tmp = numbers[i];
                    numbers[i] = numbers[j];
                    numbers[j] = tmp;
                }
            }
        }
        StringBuilder result = new StringBuilder();
        for (int i = 0; i < numbers.length; i++) {
            result.append(numbers[i]);
        }
        return result.toString();
    }
    private int dealNum(int dealnum,int length) {
        StringBuilder sb = new StringBuilder();
        sb.append(dealnum);
        int circle = length/String.valueOf(dealnum).length();
        int divider =  length%String.valueOf(dealnum).length();
        for(int i = 0;i

算法思路二：
       先将整型数组转换成String数组，然后将String数组排序，最后将排好序的字符串数组拼接出来。关键就是制定排序规则。
       排序规则如下： 
       若ab > ba 则 a > b；若ab < ba 则 a < b；若ab = ba 则 a = b；解释说明： 比如 "3" < "31"但是 "331" > "313"，所以要将二者拼接起来进行比较
代码示例二：

public class Solution {
    public String PrintMinNumber(int [] numbers) {
        if(numbers == null || numbers.length == 0) return "";
        int len = numbers.length;
        String[] str = new String[len];
        StringBuilder sb = new StringBuilder();
        for(int i = 0;i() {
            @Override
            public int compare(String o1, String o2) {
                String c1 = o1+o2;//332
                String c2 = o2+o1;//323
                return c1.compareTo(c2);
//                如果指定的数与参数相等返回0。如果指定的数小于参数返回 -1。
//                如果指定的数大于参数返回 1,如果不能理解的话想一想Arrays.sort自然排序的
           }
        });
        for(int i = 0;i

（**）面试题49：丑数
题目描述：
        把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
算法思路一：
       首先从丑数的定义我们知道，一个丑数的因子只有2,3,5，那么丑数p = 2 ^ x * 3 ^ y * 5 ^ z，换句话说一个丑数一定由另一个丑数乘以2或者乘以3或者乘以5得到，那么我们从1开始乘以2,3,5，就得到2,3,5三个丑数，在从这三个丑数出发乘以2,3,5就得到4，6,10,6，9,15,10,15,25九个丑数，我们发现这种方法会得到重复的丑数，而且我们题目要求第N个丑数，这样的方法得到的丑数也是无序的。那么我们可以维护三个队列：
    （1）丑数数组： 1；乘以2的队列：2；乘以3的队列：3；乘以5的队列：5。选择三个队列头最小的数2加入丑数数组，同时将该最小的数乘以2,3,5放入三个队列；
    （2）丑数数组：1,2；乘以2的队列：4；乘以3的队列：3，6；乘以5的队列：5，10。选择三个队列头最小的数3加入丑数数组，同时将该最小的数乘以2,3,5放入三个队列；
    （3）丑数数组：1,2,3；乘以2的队列：4,6；乘以3的队列：6,9；乘以5的队列：5,10,15。选择三个队列头里最小的数4加入丑数数组，同时将该最小的数乘以2,3,5放入三个队列；
    （4）丑数数组：1,2,3,4；乘以2的队列：6，8；乘以3的队列：6,9,12；乘以5的队列：5,10,15,20。选择三个队列头里最小的数5加入丑数数组，同时将该最小的数乘以2,3,5放入三个队列；
    （5）丑数数组：1,2,3,4,5；乘以2的队列：6,8,10，乘以3的队列：6,9,12,15；乘以5的队列：10,15,20,25。选择三个队列头里最小的数6加入丑数数组，但我们发现，有两个队列头都为6，所以我们弹出两个队列头，同时将12,18,30放入三个队列；
      疑问：
      1.为什么分三个队列？
       丑数数组里的数一定是有序的，因为我们是从丑数数组里的数乘以2,3,5选出的最小数，一定比以前未乘以2,3,5大，同时对于三个队列内部，按先后顺序乘以2,3,5分别放入，所以同一个队列内部也是有序的；
      2.为什么比较三个队列头部最小的数放入丑数数组？
      因为三个队列是有序的，所以取出三个头中最小的，等同于找到了三个队列所有数中最小的。
      实现思路：
      我们没有必要维护三个队列，只需要记录三个指针显示到达哪一步；“|”表示指针,arr表示丑数数组；
（1）1
|2
|3
|5
目前指针指向0,0,0，队列头arr[0] * 2 = 2,  arr[0] * 3 = 3,  arr[0] * 5 = 5
（2）1 2
2 |4
|3 6
|5 10
目前指针指向1,0,0，队列头arr[1] * 2 = 4,  arr[0] * 3 = 3, arr[0] * 5 = 5
（3）1 2 3
2| 4 6
3 |6 9
|5 10 15
目前指针指向1,1,0，队列头arr[1] * 2 = 4,  arr[1] * 3 = 6, arr[0] * 5 = 5
………………
代码示例：

import java.util.*;
public class Solution {
  public int GetUglyNumber_Solution(int index){
         if (index == 0) return 0;
//        if (index < 7) return index;
        int p2 = 0, p3 = 0, p5 = 0, newNum = 1;
        ArrayList arr = new ArrayList<>();
        arr.add(newNum);
        while (arr.size() < index) {
            newNum = Math.min(arr.get(p2) * 2, Math.min(arr.get(p3) * 3, arr.get(p5) * 5));
            if(arr.get(p2)*2 == newNum)
                p2++;
            if(arr.get(p3)*3 == newNum)
                p3++;
            if(arr.get(p5)*5 == newNum)
                p5++;
            arr.add(newNum);
        }
        return newNum;
  }
}

面试题50：第一个只出现一次的字符
题目描述；
       在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）.
算法思路一：
       使用Java的API实现，从前到后遍历该字符串每一个字符，假如该字符第一次出现的位置str.indexOf(str.substring(i, i + 1))和该字符最后一次出现的位置相等，则返回该字符的下标。
代码示例一：

import java.util.*;
public class Solution {
    public int FirstNotRepeatingChar(String str) {
        for (int i = 0; i < str.length(); i++) {
            if (str.indexOf(str.substring(i, i + 1)) == str.lastIndexOf(str.substring(i, i + 1))) {
                return i;
            }
        }
        return -1;
    }
}

算法思路二：
       使用HashSet实现，和面试题3有点类似。使用HashSet来存储，key值为字符，value为该字符出现的次数。假设该字符未出现过，则将key和value存储进去；假设该字符出现过，先读取该字符出现的次数，次数加一之后再存储进去。第二次扫描直接访问hash表获得字符的次数，若为1，则返回该字符所在的位置。遍历结束如果还是没有次数为1的情况返回-1。
代码示例二：

    public static int FirstNotRepeatingChar(String str) {
        HashMap  map = new HashMap();
        for(int i = 0;i

（*）面试题51：数组中的逆序对
题目描述：
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007。
算法思路：
      （1）是用归并排序，排成从小到大的序列。参考帖子:https://blog.csdn.net/weixin_38244174/article/details/88763260（2）主要是计数器的计算，如果list1数组的第current1处位置的值小于list2数组的第current2处位置的值。则进行计数器累加操作， count = count + (list1.length - current1);（这是归并排序块内是有序的）；（3）因为可能计数器会超过int类型的最大值，所以每次累加之后计数器应当直接取余1000000007。
代码示例：

public class Solution {
    public int InversePairs(int[] array) {
        mergesort(array);
        return count;
    }
    int count = 0;
    private void mergesort(int[] lists) {
        if (lists.length > 1) {
            //拆分前一半
            int[] fitrsthalf = new int[lists.length / 2];
            System.arraycopy(lists, 0, fitrsthalf, 0, lists.length / 2);
            mergesort(fitrsthalf);
            int sencondlength = lists.length - lists.length / 2;
            int[] secondhalf = new int[sencondlength];
            System.arraycopy(lists, lists.length / 2, secondhalf, 0, sencondlength);
            mergesort(secondhalf);
            merge(fitrsthalf, secondhalf, lists);
        }
    }
    private void merge(int[] list1, int[] list2, int[] temp) {
        int current1 = 0;//list1开始位置
        int current2 = 0;//list2开始位置
        int current3 = 0;//list3开始位置
        while (current1 < list1.length && current2 < list2.length) {
            if (list1[current1] < list2[current2]) {
                temp[current3++] = list1[current1++];
            } else {
                count = count + (list1.length - current1);
                count = count %1000000007;
                temp[current3++] = list2[current2++];
            }
        }
        while (current1 < list1.length)
            temp[current3++] = list1[current1++];
        while (current2 < list2.length)
            temp[current3++] = list2[current2++];
    }
}

（*）面试题52：两个链表的第一个公共结点
题目描述：
       输入两个链表，找出它们的第一个公共结点。
算法思路一：
       暴力破解法，在第一个链表上顺序遍历每个节点，每遍历到一个节点，就在第二个链表上顺序遍历每一个节点，如果第二个链表上有一个节点和第一个链表上的节点一样，这说明两个链表在该节点处重合，就找到它们的公共节点。若第一个链表长度为m，第二链表长度为n，则时间复杂度为O(m,n)。
代码示例一：

public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        ListNode p1 = pHead1;
        ListNode p2 = pHead2;
        while(p1!=null){
           p2 = pHead2; 
           while(p2!=null){
              if(p1.val == p2.val) return p1;
              p2 = p2.next;
           }
           p1= p1.next;
        }
        return null;
    }
}

算法思路二：
       如果存在共同节点的话，那么从该节点，两个链表之后的元素都是相同的。也就是说两个链表从尾部往前到某个点，节点都是一样的。我们可以用两个栈分别来装这两条链表。一个一个比较出来的值。找到第一个相同的节点。
代码示例二:

public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        if (pHead1 == null || pHead2 == null) return null;
        Stack stack1 = new Stack<>();
        Stack stack2 = new Stack<>();
        while (pHead1 != null) {
            stack1.push(pHead1);
            pHead1 = pHead1.next;
        }
        while (pHead2 != null) {
            stack2.push(pHead2);
            pHead2 = pHead2.next;
        }
        ListNode commonListNode = null;
        while (!stack1.isEmpty() && !stack2.isEmpty() && stack1.peek() == stack2.peek()){
            stack2.pop();
            commonListNode = stack1.pop();
        }
        return commonListNode;
    }
}

算法思路三：
       假定 List1长度: a+n  List2 长度:b+n, 且 a=b.时间复杂度O(n+a+b)。
代码示例三：

    public static ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        ListNode p1 = pHead1, p2 = pHead2;
        while (p1 != p2) {
            if (p1 != null) p1 = p1.next;
            if (p2 != null) p2 = p2.next;
            if (p1 == null && p2 != null) p1 = pHead2;
            if (p2 == null && p1 != null) p2 = pHead1;
        }
        return p1;
    }