摘要:
「平衡二叉查找树(Balance Binary Search Tree)」用以解决二叉查找树因不平衡情况而导致的执行效率下降问题,不过为了提高整体操作的效率,基本上使用非严格的平衡二叉查找树,代表是「红黑树(Red-Black Tree)」。
平衡才是美
前面关于二叉查找树的文章已经提到过,平衡情况下二叉查找树的时间复杂度才是 ,但按照之前二叉查找树的插入、删除操作听之任之,不加以干预,二叉查找树的平衡性迟早会被破坏,于是引入了平衡二叉查找树。
对平衡二叉查找树的定义是树中任意节点的左右子树高度之差不大于 1,这样可以确保某个子树不会高度过大,影响二叉查找树的平衡。节点可以通过存储左右子树高度差确定是否符合平衡的定义,当插入或者删除操作时更新相应节点的高度,而查找操作并不受到影响。
不平衡到平衡
上一小节已经告诉我们如何确定一棵树是否平衡,或者树中的某个节点是否保持平衡,但如果出现不平衡的情况我们需要如何将其转换为平衡状态?一般「左旋」「右旋」是解决此问题的方法,其实左旋应该称为以某个节点为中心向左旋转,右旋与之相对应,应该被称为以某个节点为中心向右旋转,在左旋和右旋的操作中一般会有两个关键的节点,一个为「root」节点,一个为「pivot」节点,此处的 root 并不是指树的根节点,可以是树中的任意节点,可以理解为以此节点为根节点,左旋和右旋的操作就是以 pivot 节点为中心节点进行左右旋转。
几种不平衡情况
虽然二叉查找树有多种不平衡的具体情况,但最终被抽象总结为四种情况,接下来我们一起分析一下。
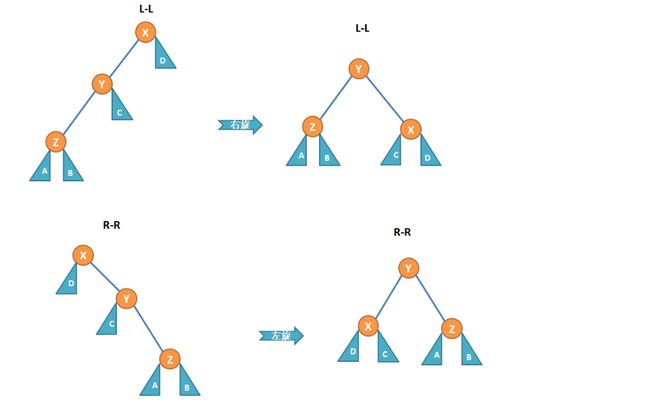
左-左(L-L)
此情况下 root 节点的左子树高度大于右子树,且高度差大于 1,而 pivot 为 root 的左子节点,而导致不平衡的是此节点的左子树,此时为了保持平衡需要进行右旋操作,将 root 移至 pivot 右子节点,pivot 的右子节点移至 root 的左子节点。
为何这样旋转?因为将 pivot 右旋时 pivot 会顶替 root 节点位置,所以 root 节点需要重新放置,按照二叉查找树的规则,pivot 是 root 的左子节点,root 节点值大于 pivot 值,root 节点应该放置在 pivot 的右子节点。如果 pivot 本身存在右子节点,那右子节点的位置将被 root 节点顶替,也需要重新放置。作为 pivot 的右子节点数值肯定大于 pivot 节点,而此节点依然属于原 root 节点的左子树,数值小于 root 节点,所以此节点应该放置于 root 节点的 左子节点处。
右-右(R-R)
右-右情况正好与左-左情况相反,当然也使用相反的旋转——右旋,将 root 节点移至 pivot 节点的左子节点处,将 pivot 节点的原左子节点移至 root 节点的右子节点,当然原因与左-左情况的相似。除了这两种情况外还有另外两种情况,分别是「左-右(L-R)」「右-左(R-L)」,左-右需要先进行左旋再进行右旋,右-左要先进行右旋再进行左旋,具体情况可以根据下图分析。
[图片上传失败...(image-a0c404-1569162501263)]
AVL 树
AVL 树是平衡二叉查找树的代表,通过左右子树的高度差来判断是否平衡,如果出现不平衡情况,需要根据具体非平衡形态进行相应的左右旋操作,但平衡二叉查找树的节点需要存储该节点的高度,所以每个节点的父节点可以通过左右子节点的高度属性快速判断左右子树是否出现了不平衡。在平衡性的实现上我采用左子树高度减右子树高度的方式,相减结果等于 0 表示两个子树高度一致,当结果大于 1 时表示左子树更高,当结果小于 -1 时表示右子树更高,这样的结果更加有利于判断当前树状处于哪种不平衡形态下。
代码实现
public class AvlTree {
private Node root;
public Node insertNode(Node node, int num) {
if (node == null) {
Node leaf = new Node(num);
if (root == null) {
root = leaf;
}
return leaf;
}
if (num < node.data) {
node.left = insertNode(node.left, num);
} else if (num > node.data) {
node.right = insertNode(node.right, num);
} else {
return node;
}
int balance = getBalance(node);
if (balance > 1 && num < node.left.data) {
rotateRight(node);
} else if (balance < -1 && num > node.right.data) {
rotateLeft(node);
} else if (balance > 1 && num > node.left.data) {
rotateLeft(node.left);
rotateRight(node);
}
node.height = updateNodeHeight(node);
return node;
}
private int getNodeHeight(Node node) {
return node == null ? 0 : node.height;
}
public List sortNode() {
List nodes = new ArrayList<>();
getSortNodes(nodes, root);
return nodes;
}
private void getSortNodes(List sortNodes, Node node) {
if (node == null) {
return;
}
if (node.left == null && node.right == null) {
sortNodes.add(node);
return;
}
getSortNodes(sortNodes, node.left);
sortNodes.add(node);
getSortNodes(sortNodes, node.right);
}
public int getBalance(Node node) {
return getNodeHeight(node.left) - getNodeHeight(node.right);
}
public Node getRoot() {
return root;
}
public int getHeight() {
return root.height;
}
public void rotateRight(Node rRoot) {
Node pivot = rRoot.left;
Node pivotR = pivot.right;
pivot.right = rRoot;
rRoot.left = pivotR;
updateRotateNodeState(rRoot, pivot);
}
private void updateRotateNodeState(Node rRoot, Node pivot) {
rRoot.height = updateNodeHeight(rRoot);
pivot.height = updateNodeHeight(pivot);
if (rRoot == root) {
root = pivot;
}
}
private int updateNodeHeight(Node rRoot) {
return 1 + Math.max(getNodeHeight(rRoot.left), getNodeHeight(rRoot.right));
}
public void rotateLeft(Node rRoot) {
Node pivot = rRoot.right;
Node pivotL = pivot.left;
pivot.left = rRoot;
rRoot.right = pivotL;
updateRotateNodeState(rRoot, pivot);
}
public class Node {
public final int data;
private Node left;
private Node right;
private int height = 1;
public Node(int data) {
this.data = data;
}
}
}
AVL 树的实现代码中只是实现了插入节点的操作,删除节点与之类似,按照二叉树删除节点的的规则将节点删除后判断节点是否处于平衡状态,如果未处于平衡状态就根据非平衡形态进行相应的旋转操作。
非严格平衡二叉树
虽然 AVL 树利用节点的旋转保持了整个树的平衡,但是每次插入节点或者删除节点都需要进行相关节点的旋转操作,必然会使操作效率下降,为了在二叉树的平衡性与执行效率之间找到一个平衡点,就提出了非严格定义的平衡二叉树,这样的二叉树不需要遵守任意节点的左右子树高度差不大于 1 的规定,而只要保持高度与 不会相差过大即可。
说理论过于抽象,我们举个实际的例子,比如非严格平衡二叉查找树的代表——「红黑树(Red-Black Tree/R-B Tree)」,红黑树也是二叉树,不同的是它的节点会是红色或者黑色,一棵红黑树需要满足以下几个条件
- 根节点必须为黑色节点
- 叶子节点都是黑色的空节点(NIL)
- 两个相邻节点不能同时为红色节点,也就是说红色节点都是被黑色节点隔开的
- 从任意节点出发,到达其可达的叶子节点路径上的黑色节点数量相同
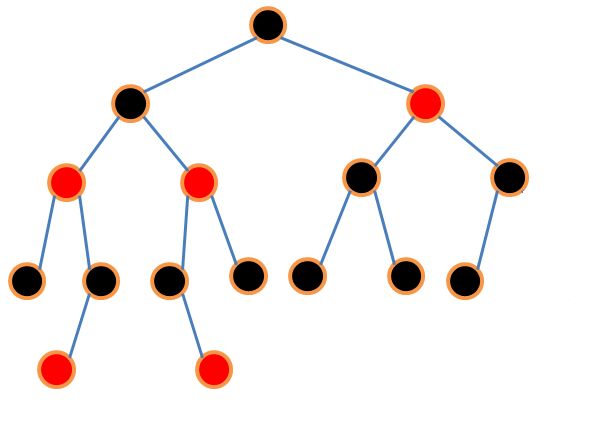
第 1,3,4 点都比较容易理解,第 2 条保证叶子节点都为黑色空节点是为了简化红黑树的实现,现在的分析我们可以暂时不关心第 2 个定义,按照规则我们可以画一棵红黑树。
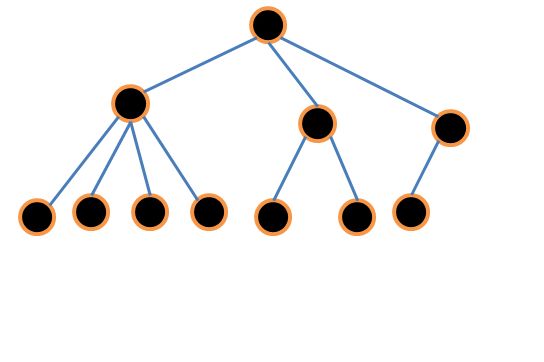
那红黑树的平均高度是多少?我们可以先把红色节点移除,使黑色节点形成四叉树,将四叉树节点移动转换为完全二叉树时可以看出,四叉树高度是低于相同节点数量下的完全二叉树的,也就是只由黑色节点组成的四叉树高度是低于 的,因为相邻红色节点需要被黑色节点隔开,加入红色后的红黑树高度是低于 的,其实也是相对平衡的,并且在保持平衡的情况下使插入和删除操作都保持了较高的执行效率,如果红黑树碰到破坏平衡的情况,也就是破坏红黑树的第 3,4 条定义时可以按照红黑树的对应操作步骤使用左右旋使其重新符合定义。
[图片上传失败...(image-d39c98-1569162501263)]
通过红黑树我们可以看出其实平衡的定义可以比较宽泛,我们希望解决的二叉查找树平衡性问题其实是防止其退化为链表,也就是左右子树的高度差距极大,而保持平衡其实是在保持二叉查找树的对称性,避免高度差距极大的左右子树情况,降低二叉查找树的整体高度,以此保证二叉查找树的执行效率。
总结
由于平衡性问题会极大影响二叉查找树的执行效率,业界以左右子树高度差不大于 1 作为二叉查找树的界定标准,通过左旋或者右旋的方式来维护树的平衡,AVL 树是这种严格定义平衡二叉查找树代表,不过为了保持平衡导致操作的效率受到影响,为了平衡这种影响,业界采用更加广泛的平衡定义,同时也衍生出红黑树这样的非严格定义的平衡二叉查找树代表,在操作性能和平衡性之间找到了平衡点。
文章中如有问题欢迎留言指正
本章节代码已经上传GitHub,可点击跳转查看代码详情。
数据结构与算法之美笔记系列将会做为我对王争老师此专栏的学习笔记,如想了解更多王争老师专栏的详情请到极客时间自行搜索。