Xilinx-Verilog-学习笔记（20）：汉明码编解码与CRC冗余校验

Xilinx-Verilog-学习笔记（20）：汉明码编解码与CRC冗余校验

一、汉明码编解码

1、原理解析

汉明码（Hamming Code），是在电信领域的一种线性调试码，以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的消息流中插入验证码，当计算机存储或移动数据时，可能会产生数据位错误，以侦测并更正单一比特错误。由于汉明编码简单，它们被广泛应用于内存（RAM）。

约定N为编码后的数据比特长度，K为待编码数据的比特长度，R为校验位（R=N-K），D为最小汉明距离（相邻两行之间不同比特数据的最小值）。

生成矩阵G：

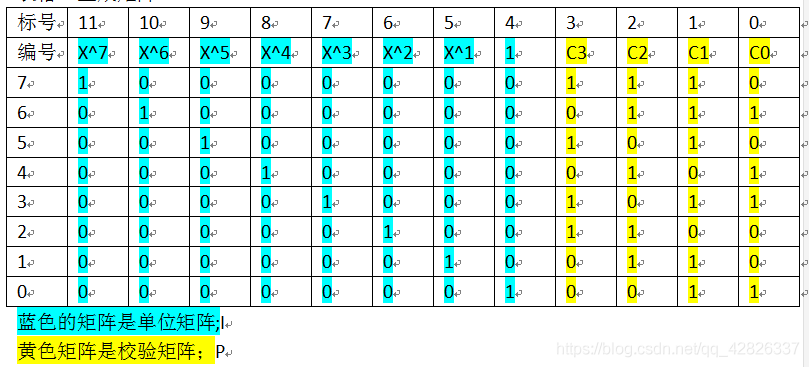
（1）编码过程
A[7:0]为原始矩阵，编码后的矩阵为CODE[11:0]=G x A
即有：
CODE[11]=A[7]
CODE[10]=A[6]
………………………
CODE[4]=A[0]
CODE[3]=A[7] ^ A[5] ^ A[3] ^ A[2]
CODE[2]=A[7] ^ A[6] ^ A[4] ^ A[2] ^ A[1]
CODE[1]=A[7] ^ A[6] ^ A[5] ^ A[3] ^ A[1] ^ A[0]
CODE[0]=A[6] ^ A[4] ^ A[3] ^ A[0]
其中 ^表示异或

举例：

待编码数据为8’b0011_0101

则矩阵A为一维的[0 0 1 1 0 1 0 1]；
编码过程为：
CODE[11]=A[7]=0
CODE[10]=A[6]=0
CODE[9]=A[5]=1
CODE[8]=A[4]=1
CODE[7]=A[3]=0
CODE[6]=A[2]=1
CODE[5]=A[1]=0
CODE[4]=A[0]=1
CODE[3]=A[7] ^ A[5] ^ A[3] ^ A[2]=0 ^ 1 ^ 0 ^ 1=0
CODE[2]=A[7] ^ A[6] ^ A[4] ^ A[2] ^ A[1]=0 ^ 0 ^ 1 ^ 1 ^ 0=0
CODE[1]=A[7] ^ A[6] ^ A[5] ^ A[3] ^ A[1] ^ A[0]=0 ^ 0 ^ 1 ^ 0 ^ 0 ^ 1=0
CODE[0]=A[6] ^ A[4] ^ A[3] ^ A[0]=0 ^ 1 ^ 0 ^ 1=0

编码后数据U为12’b0011_0101_0000=12’h350

（2）解码过程
解码分为四步：第一步是求校验矩阵，第二步是求校正子，第三步是定位错误比特，第四步是优化数据修正方法。

第一步：求校验矩阵

校验矩阵用字母H表示，H={P^T,I(N-K)}，其中I(N-K)代表4 x 4的单位矩阵。
校验矩阵H为：

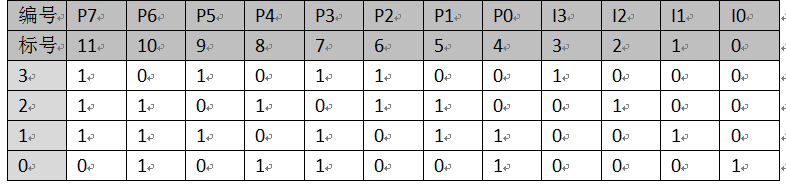
第二步：求校正子

假设经过信道后出来的数据U’变为12’b0011_0101_0001=12’h351
校正子用字母S表示，待解码数据为CODE用U表示。S=H^T * U
即有：
S[3]=U[11] ^ U[9] ^ U[7] ^ U[6] ^ U[3]=0 ^ 1 ^ 0 ^ 1 ^ 0=0
S[2]=U[11] ^ U[10] ^ U[8] ^ U[6] ^ U[5] ^ U[2]=0 ^ 0 ^ 1 ^ 1 ^ 0 ^ 0=0
S[1]=U[11] ^ U[10] ^ U[9] ^ U[7] ^ U[5] ^ U[4] ^ U[1]=0 ^ 0 ^ 1 ^ 0 ^ 0 ^ 1 ^ 0=0
S[0]=U[10] ^ U[8] ^ U[7] ^ U[4] ^ U[0]=0 ^ 1 ^ 0 ^ 1 ^ 1=1

得到的矫正因子S为0001

第三步：定位错误比特

通过错误模式推得校正子Si， i是index指的的是错误模式的种类，因为我们汉明码解码数据有12bit 所以错误模式有12种，还包括一种全部正确的模式。
Si=H^T*Ei

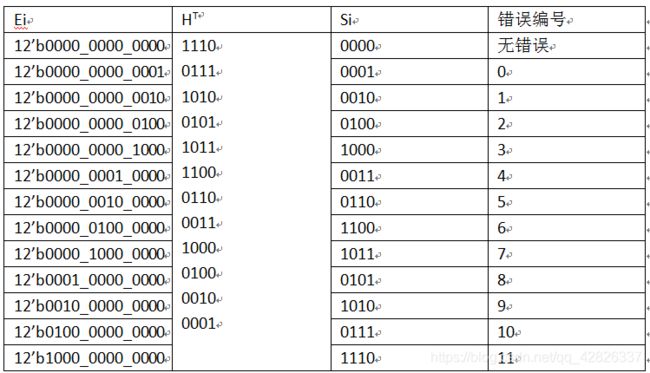
已知错误的比特位为最低位的0变成了1，且计算得到的S为0001，查找错误表可知是编号0.对应可以看出是第0比特位出现了错误。

第四步：优化数据修正方法
修正后的矩阵C为：
C[11]=U[11]^( ~S[3]&S[2]&S[1]&S[0])
C[10]=U[10]^(S[3]& ~S[2]&S[1]& ~S[0])
C[9]=U[9]^( ~S[3]&S[2]& ~S[1]&S[0])
C[8]=U[8]^(S[3]&S[2]&S[1]&S[0])
C[7]=U[7]^(S[3]& ~S[2]&S[1]&S[0])
C[6]=U[6]^(S[3]&S[2]& ~S[1]& ~S[0])
C[5]=U[5]^( ~S[3]&S[2]&S[1]& ~S[0])
C[4]=U[4]^( ~S[3]& ~S[2]&S[1]&S[0])
C[3]=U[3]^(S[3]& ~S[2]& ~S[1]& ~S[0])
C[2]=U[2]^( ~S[3]&S[2]& ~S[1]& ~S[0])
C[1]=U[1]^( ~S[3]& ~S[2]&S[1]& ~S[0])
C[0]=U[0]^( ~S[3]& ~S[2]& ~S[1]&S[0])

待解码U12’b0011_0101_0001=12’h351，S为0001
则修正后的C为：
C[11]=U[11]^( ~S[3]&S[2]&S[1]&S[0])=0 ^ 0=0
C[10]=U[10]^(S[3]& ~S[2]&S[1]& ~S[0])=0 ^ 0=0
C[9]=U[9]^( ~S[3]&S[2]& ~S[1]&S[0])=1 ^ 0=1
C[8]=U[8]^(S[3]&S[2]&S[1]&S[0])=1 ^ 0=1
C[7]=U[7]^(S[3]& ~S[2]&S[1]&S[0])=0 ^ 0=0
C[6]=U[6]^(S[3]&S[2]& ~S[1]& ~S[0])=1 ^ 0=1
C[5]=U[5]^( ~S[3]&S[2]&S[1]& ~S[0])=0 ^ 0=0
C[4]=U[4]^( ~S[3]& ~S[2]&S[1]&S[0])=1 ^ 0=1
C[3]=U[3]^(S[3]& ~S[2]& ~S[1]& ~S[0])=0 ^ 0=0
C[2]=U[2]^( ~S[3]&S[2]& ~S[1]& ~S[0])=0 ^ 0=0
C[1]=U[1]^( ~S[3]& ~S[2]&S[1]& ~S[0])=0 ^ 0=0
C[0]=U[0]^( ~S[3]& ~S[2]& ~S[1]&S[0]) =1 ^ 1=0

则经过修正后的C为12’b0011_0101_0000
可以发现最后被错写为1的已经被重新修正为0。

2、design文件

（1）汉明码编码：hamm_code.v

module	hamm_code(
	input	wire			sclk,
	input	wire			rst_n,
	input	wire			data_v,	//接收到标志进行一次转码
	input	wire	[7:0]	data_i,	//待编码数据
	output	reg				code_v, //编码标志位
	output	reg		[11:0]	code_o	//编码后数据
);

always @(posedge sclk or negedge rst_n)
	if(rst_n == 1'b0)
		code_v <= 1'b0;
	else code_v <= data_v;
	
always @(posedge sclk or negedge rst_n)
	if(rst_n == 1'b0)
		code_o<='d0;
	else if(data_v == 1'b1)begin
		code_o[11:4] <= data_i;
		code_o[3] <= data_i[7]^data_i[5]^data_i[3]^data_i[2];
		code_o[2] <= data_i[7]^data_i[6]^data_i[4]^data_i[2]^data_i[1];
		code_o[1] <= data_i[7]^data_i[6]^data_i[5]^data_i[3]^data_i[1]^data_i[0];
		code_o[0] <= data_i[6]^data_i[4]^data_i[3]^data_i[0];
	end
	else
		code_o <= 'd0;
endmodule

（2）汉明码解码：hamm_dec.v

module	hamm_dec(

	input	wire			sclk,
	input	wire			rst_n,
	input	wire	[11:0]	data_i,
	input	wire			data_v,
	output	reg		[7:0]	data_o,
	output	reg				data_ov
);

wire	[3:0]	S;
wire	[11:0]	C;

always @(posedge sclk or negedge rst_n)
	if(rst_n == 1'b0)
		data_ov <= 1'd0;
	else data_ov <= data_v;

assign S[3]=data_i[11]^data_i[9]^data_i[7]^data_i[6]^data_i[3];
assign S[2]=data_i[11]^data_i[10]^data_i[8]^data_i[6]^data_i[5]^data_i[2];
assign S[1]=data_i[11]^data_i[10]^data_i[9]^data_i[7]^data_i[5]^data_i[4]^data_i[1];
assign S[0]=data_i[10]^data_i[8]^data_i[7]^data_i[4]^data_i[0];

assign	C[11]=data_i[11]^(S[3]&S[2]&S[1]&~S[0]); 
assign	C[10]=data_i[10]^(~S[3]&S[2]&S[1]&S[0]);
assign	C[9]=data_i[9]^(S[3]&~S[2]&S[1]&~S[0]);  
assign	C[8]=data_i[8]^(~S[3]&S[2]&~S[1]&S[0]) ;   
assign	C[7]=data_i[7]^(S[3]&~S[2]&S[1]&S[0]);   
assign	C[6]=data_i[6]^(S[3]&S[2]&~S[1]&~S[0]);  
assign	C[5]=data_i[5]^(~S[3]&S[2]&S[1]&~S[0]) ; 
assign	C[4]=data_i[4]^(~S[3]&~S[2]&S[1]&S[0]);  
assign	C[3]=data_i[3]^(S[3]&~S[2]&~S[1]&~S[0]); 
assign	C[2]=data_i[2]^(~S[3]&S[2]&~S[1]&~S[0]); 
assign	C[1]=data_i[1]^(~S[3]&~S[2]&S[1]&~S[0]);
assign	C[0]=data_i[0]^(~S[3]&~S[2]&~S[1]&S[0]) ;

always @(posedge sclk or negedge rst_n)
	if(rst_n == 1'b0)
		data_o<= 'd0;
	else if(data_v == 1'b1)
		data_o <= C[11:4];
	else
		data_o <='d0;

endmodule

3、testbench文件

`timescale	1ns/1ns
module	tb_hamming;

reg				sclk ,rst_n;
reg		[7:0]	data;
reg				data_v;
wire	[11:0]	code;
wire			code_v;
wire	[7:0]	c_data;
wire			c_v;
initial	begin    
	rst_n =0;
	sclk =0;
	
	#100
	rst_n=1;
end

always # 10 sclk = ~sclk;

initial begin
	data =0;
	data_v =0;
	#300
	@(posedge sclk)
	data_v =1;  
	data =8'h35;
	#22
	data_v =0;   
 	data =8'h0;
end    


hamm_code	hamm_code_inst(

	.sclk		(sclk),
	.rst_n		(rst_n),
	.data_v		(data_v),
	.data_i		(data),//待编码数据
	.code_v		(code_v),
	.code_o		(code)//编码后数据
	
);


hamm_dec	hamm_dec_inst(

	.sclk		(sclk),
	.rst_n		(rst_n),
	.data_i		({
     code[11:1],~code[0]}),
	//.data_i		({
     ~code[11],code[10:0]}),
	.data_v		(code_v),
	.data_o		(c_data),
	.data_ov	(c_v)
);

endmodule

4、仿真波形

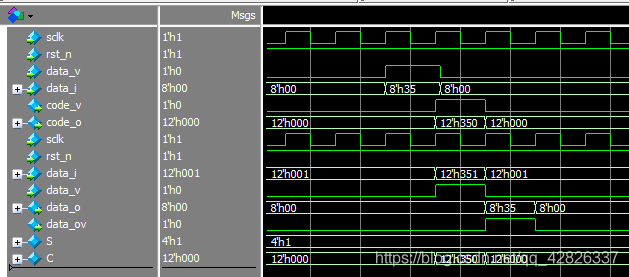
原始数据data_i为8’h35，通过汉明码编码为code_o=12’h350。此时该数据经过信道，我们模拟最低位翻转了，即从信道输出data_i为12’h351，汉明码自动校验发现错误，并对其进行修正变为C=12‘h350，最终解码后的数据重新恢复为8’h35。

二、CRC冗余校验

1、原理解析

CRC8基本原理
计算方法

举例：
生成多项式G（x）=x⁴+x¹+x⁰
则G（x）=10011
编码后的矩阵CODE：1010111011

（1）将码字CODE左移4位（最高次幂）：10101110110000
（2）将左移4位的与G（x）相除：

（3）从结果可得：CRC=0010，将这部分加到编码矩阵后面，则为1010111011_0010
（4）在接收端同样需要进行验证，如果余数为0则表示正确。

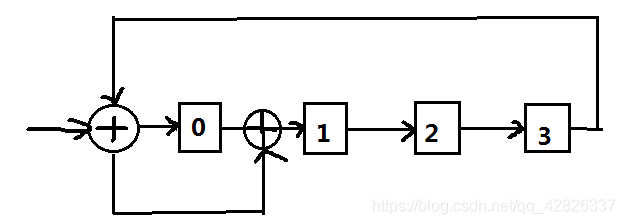
2、硬件电路实现

画出多项式的硬件结构电路图：

画的方法是：CRC=10011，只要是有1的位，前面就要放一个异或，那么第0位和第1位前面有异或，最高位和最低位共用1个异或，所以在图中没有体现。最高位域输入的异或后的结果，要反馈到每个异或的地方去。

最后推出各个比特位下的多项式公式即可。