C语言算法——排序
这里偷了一张图
目录
- 快速排序!!!
- 冒泡排序
- 桶排序
- 选择排序
- 插入排序
- 堆排序(目前看不懂)
快速排序!!!
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要Ο(n logn)次比较。在最坏状况下则需要Ο(n2)次比较,但这种状况并不常见。事实上,快速排序通常明显比其他Ο(n log n) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
算法步骤:
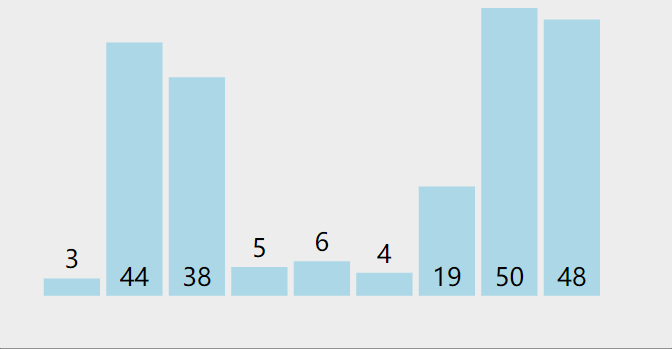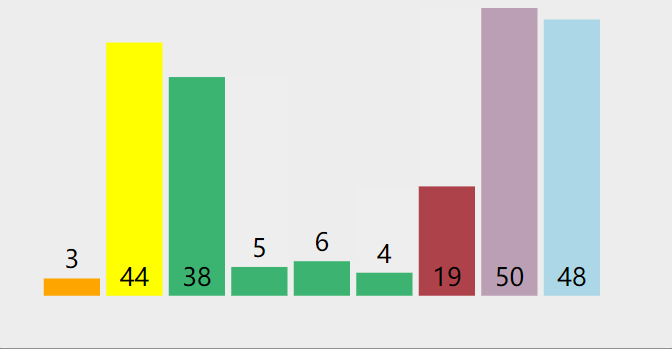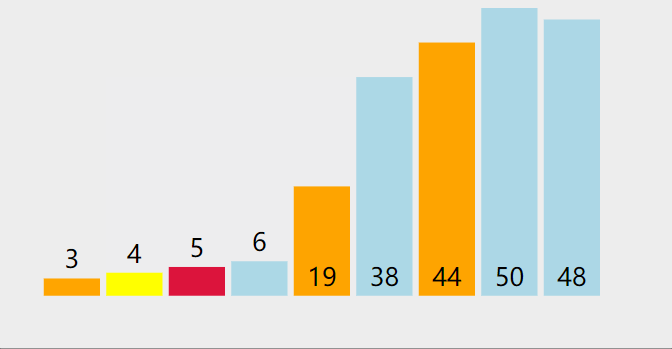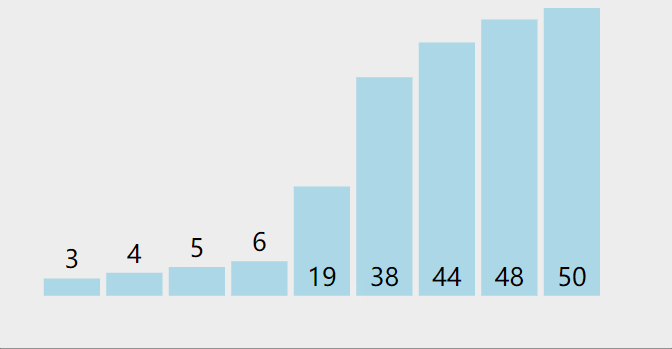
- 从数列中挑出一个元素,称为 “基准”(pivot)。
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
- 递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
int partition(int a[], int low, int high)
{
int privotKey = a[low]; //基准元素
while(low < high){
//从表的两端交替地向中间扫描
while(low < high && a[high] >= privotKey) --high; //从high 所指位置向前搜索,至多到low+1 位置。将比基准元素小的交换到低端
swap(&a[low], &a[high]);
while(low < high && a[low] <= privotKey ) ++low;
swap(&a[low], &a[high]);
}
print(a,10);
return low;
}
void quickSort(int a[], int low, int high){
if(low < high){
int privotLoc = partition(a, low, high); //将表一分为二
quickSort(a, low, privotLoc -1); //递归对低子表递归排序
quickSort(a, privotLoc + 1, high); //递归对高子表递归排序
}
}
int main(){
int a[10] = {
3,1,5,7,2,4,9,6,10,8};
cout<<"初始值:";
print(a,10);
quickSort(a,0,9);
cout<<"结果:";
print(a,10);
}
冒泡排序
冒泡遍历所有的数据,每次对相邻元素进行两两比较,如果顺序和预先规定的顺序不一致,则进行位置交换;这样一次遍历会将最大或最小的数据上浮到顶端,之后再重复同样的操作,直到所有的数据有序。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端。
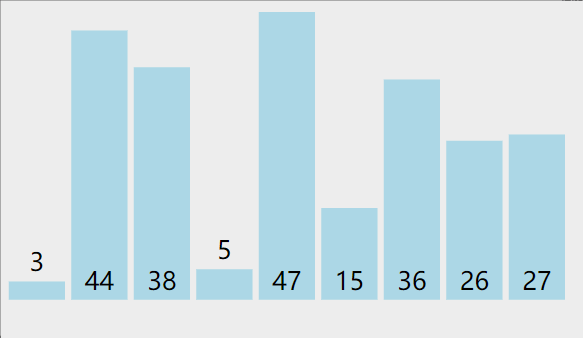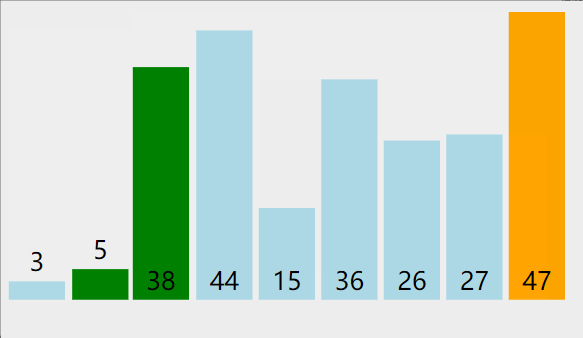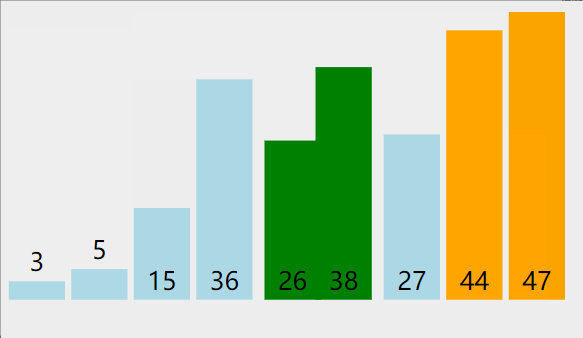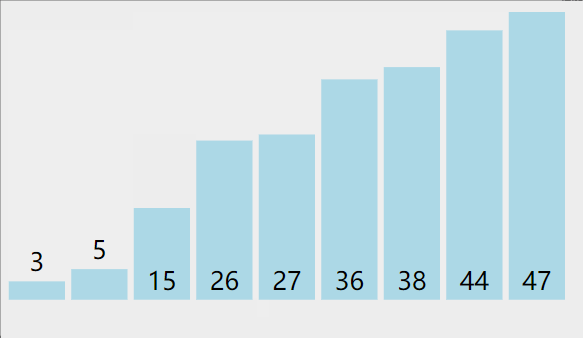
#include 桶排序
准备桶的时候,桶的大小是原来排序数组中最大元素的值加一,然后遍历无序的数组,把无序数组中的元素的值当成下标给到桶,每存在一个值,桶中的数量就加一。输出的时候,桶的下标值就是之前需要排序的数组的值,只有桶中的数量大于等于一的时候才表示有数据,再进行输出
简单地说: 待排序数组 分配到若干个桶 各自执行排序任务
#include 选择排序
简单选择排序的实现思想:比较+交换
- 从待排序序列中,找到关键字最小的元素;
- 如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
- 从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束。因此我们可以发现,简单选择排序也是通过两层循环实现。 第一层循环:依次遍历序列当中的每一个元素。第二层循环:将遍历得到的当前元素依次与余下的元素进行比较,符合最小元素的条件,则交换。
void print(int a[], int n ,int i){
cout<<"第"<<i+1 <<"趟 : ";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
/**
* 数组的最小值
*
* @return int 数组的键值
*/
int SelectMinKey(int a[], int n, int i)
{
int k = i;
for(int j=i+1 ;j< n; ++j) {
if(a[k] > a[j]) k = j;
}
return k;
}
/**
* 选择排序
*
*/
void selectSort(int a[], int n){
int key, tmp;
for(int i = 0; i< n; ++i) {
key = SelectMinKey(a, n,i); //选择最小的元素
if(key != i){
tmp = a[i]; a[i] = a[key]; a[key] = tmp; //最小元素与第i位置元素互换
}
print(a, n , i);
}
}
int main(){
int a[8] = {
3,1,5,7,2,4,9,6};
cout<<"初始值:";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl<<endl;
selectSort(a, 8);
print(a,8,8);
}
插入排序
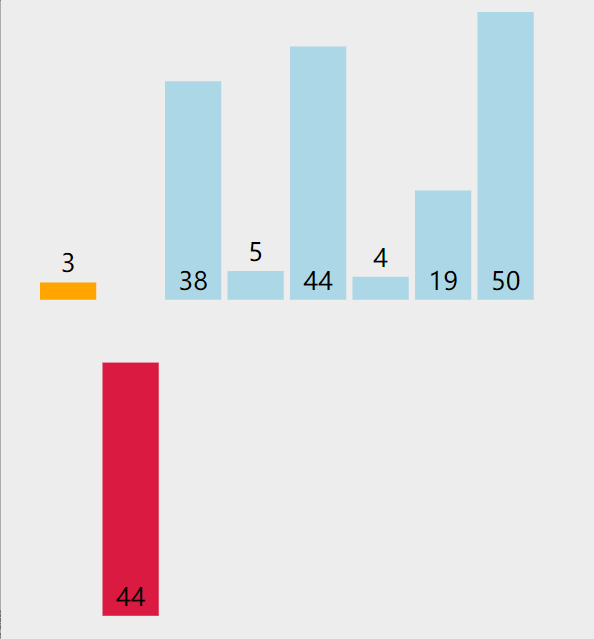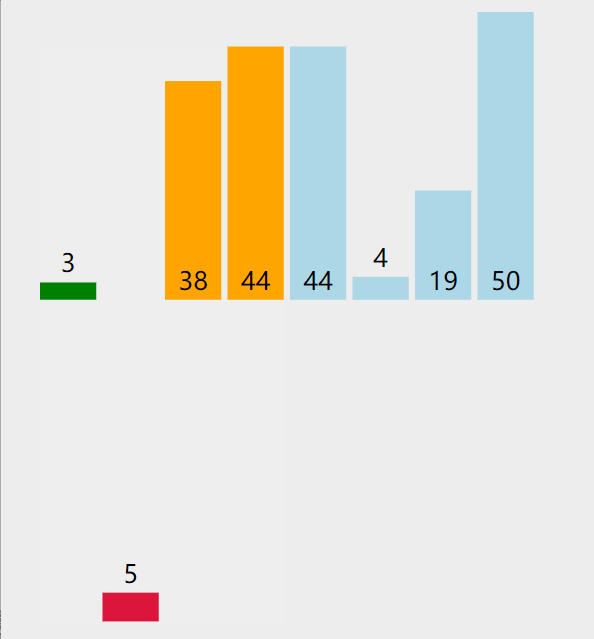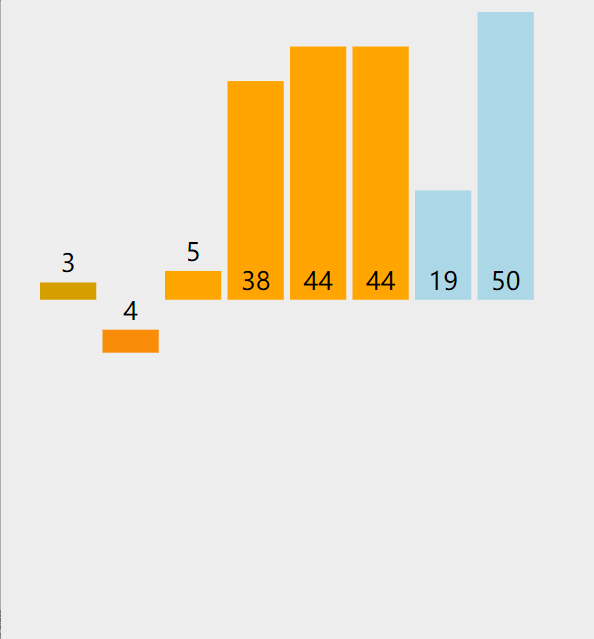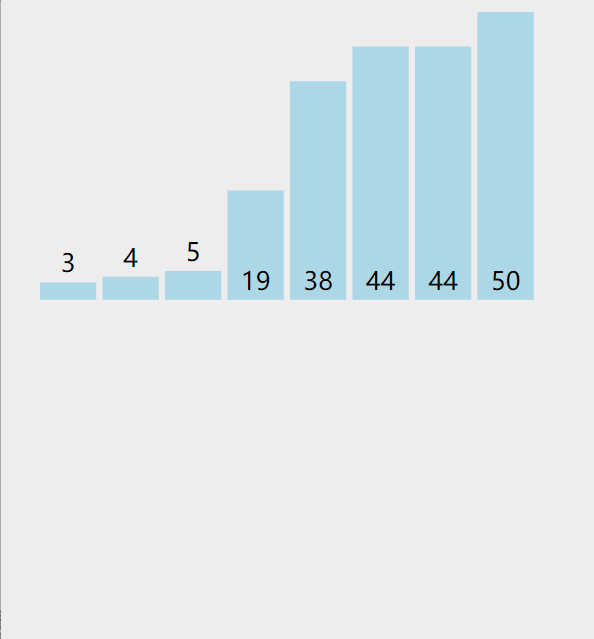
选择元素,插入有序数组
直接插入排序的核心思想就是:将数组中的所有元素依次跟前面已经排好的元素相比较,如果选择的元素比已排序的元素小,则交换,直到全部元素都比较过 因此,从上面的描述中我们可以发现,直接插入排序可以用两个循环完成:
第一层循环:遍历待比较的所有数组元素
第二层循环:将本轮选择的元素(selected)与已经排好序的元素(ordered)相比较。 如果:selected > ordered,那么将二者交换。
void print(int a[], int n ,int i){
cout<<i <<":";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void InsertSort(int a[], int n)
{
for(int i= 1; i<n; i++){
if(a[i] < a[i-1]){
//若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入
int j= i-1;
int x = a[i]; //复制为哨兵,即存储待排序元素
a[i] = a[i-1]; //先后移一个元素
while(x < a[j]){
//查找在有序表的插入位置
a[j+1] = a[j];
j--; //元素后移
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i); //打印每趟排序的结果
}
}
int main(){
int a[8] = {
3,1,5,7,2,4,9,6};
InsertSort(a,8);
print(a,8,8);
}
堆排序(目前看不懂)
堆的概念
堆:本质是一种数组对象。特别重要的一点性质:任意的叶子节点小于(或大于)它所有的父节点。对此,又分为大顶堆和小顶堆:
大顶堆要求节点的元素都要大于其孩子。
小顶堆要求节点元素都小于其左右孩子。
两者对左右孩子的大小关系不做任何要求。
利用堆排序,就是基于大顶堆或者小顶堆的一种排序方法。下面,我们通过大顶堆来实现。
基本思想: 堆排序可以按照以下步骤来完成:
1. 首先将序列构建称为大顶堆; (这样满足了大顶堆那条性质:位于根节点的元素一定是当前序列的最大值)
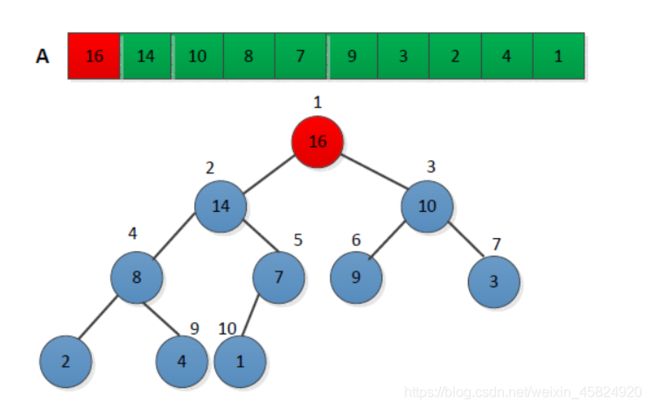
2. 取出当前大顶堆的根节点,将其与序列末尾元素进行交换;(此时:序列末尾的元素为已排序的最大值;由于交换了元素,当前位于根节点的堆并不一定满足大顶堆的性质)
3. 对交换后的n-1个序列元素进行调整,使其满足大顶堆的性质;

4. 重复2.3步骤,直至堆中只有1个元素为止
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
/**
* 已知H[s…m]除了H[s] 外均满足堆的定义
* 调整H[s],使其成为大顶堆.即将对第s个结点为根的子树筛选,
*
* @param H是待调整的堆数组
* @param s是待调整的数组元素的位置
* @param length是数组的长度
*/
void HeapAdjust(int H[],int s, int length)
{
int tmp = H[s];
int child = 2*s+1; //左孩子结点的位置。(i+1 为当前调整结点的右孩子结点的位置)
while (child < length) {
if(child+1 <length && H[child]<H[child+1]) {
// 如果右孩子大于左孩子(找到比当前待调整结点大的孩子结点)
++child ;
}
if(H[s]<H[child]) {
// 如果较大的子结点大于父结点
H[s] = H[child]; // 那么把较大的子结点往上移动,替换它的父结点
s = child; // 重新设置s ,即待调整的下一个结点的位置
child = 2*s+1;
} else {
// 如果当前待调整结点大于它的左右孩子,则不需要调整,直接退出
break;
}
H[s] = tmp; // 当前待调整的结点放到比其大的孩子结点位置上
}
print(H,length);
}
/**
* 初始堆进行调整
* 将H[0..length-1]建成堆
* 调整完之后第一个元素是序列的最小的元素
*/
void BuildingHeap(int H[], int length)
{
//最后一个有孩子的节点的位置 i= (length -1) / 2
for (int i = (length -1) / 2 ; i >= 0; --i)
HeapAdjust(H,i,length);
}
/**
* 堆排序算法
*/
void HeapSort(int H[],int length)
{
//初始堆
BuildingHeap(H, length);
//从最后一个元素开始对序列进行调整
for (int i = length - 1; i > 0; --i)
{
//交换堆顶元素H[0]和堆中最后一个元素
int temp = H[i]; H[i] = H[0]; H[0] = temp;
//每次交换堆顶元素和堆中最后一个元素之后,都要对堆进行调整
HeapAdjust(H,0,i);
}
}
int main(){
int H[10] = {
3,1,5,7,2,4,9,6,10,8};
cout<<"初始值:";
print(H,10);
HeapSort(H,10);
//selectSort(a, 8);
cout<<"结果:";
print(H,10);
}
