前言
近日拜读了Daniel Shiffman先生的著作——《代码本色:用编程模拟自然系统》,决定做一组习作,来对书中提到的随机行为及牛顿运动学进行理解,并对一些实例进行拓展学习,从而提升自己相关方面的知识水平和实践能力。
《代码本色》第3章概述
在第3章中,作者向我们介绍了三角函数。三角函数会给我们带来很多新工具。本章我们会学习角、角速度以及角加速度,期间还会涉及正弦函数和余弦函数,它们可以用来制作平滑的波形曲线。有了这些知识,我们就能计算更复杂的力,而这些力往往都涉及角度,比如钟摆的摆动和盒子从斜坡滑下时所受的力。作者通过一些实例深入浅出地讲解了这些力,并对这些力进行了分析和实践。
在这一章中,我印象比较深的点是对简谐运动的模拟,此外,还有对钟摆、弹簧的模拟。下面,我将介绍我根据本章内容而创作的Processing编程习作。
习作
可以拉拽绿色点,每两个点之间都有一个弹簧效果的力支撑。此外,在其他地方点击鼠标还可以添加新的点。
创作过程
本次创作的关键在于——如何实现弹簧的效果。对此,书上花了很大篇幅进行介绍。
首先介绍下弹簧的弹力。弹簧的弹力可以根据胡克定律计算得到,胡克定律以英国物理学家罗伯特·胡克命名,他在1660年发明了这个公式。胡克最初是用拉丁文描述这个公式的——“Ut tensio,sic vis”, 这句话的意思是“力如伸长(那样变化)”。我们可以这么理解它:弹簧的弹力与弹簧的伸长量成正比。
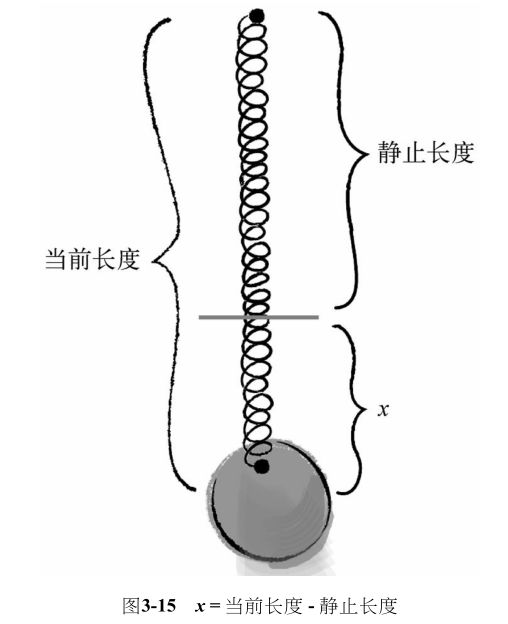
换个说法,就是我们大家都熟悉的公式:F=-kx。这里的k就是弹性系数,是一个常数。而x是当前长度与静止长度的差值。
接下来,我开始编写Spring类(弹簧类)。
首先定义了这三个变量:
PVector anchor; // 起始位置
float len;// 静止长度
float k = 0.05;//弹性系数
然后,在update()函数里计算弹力:
// 计算弹力
void update() {
PVector force = PVector.sub(a.position, b.position);//矢量指向从a点到b点
float d = force.mag();//计算向量长度
float stretch = d - len;//形变长度
force.normalize();
force.mult(-1 * k * stretch); //F=-kx
a.applyForce(force);
force.mult(-1);//牛顿第三定律
b.applyForce(force);
}
代码中有详细的注释,就不一一解释了。
此外值得一提的是,在Circle类中添加了这样一个变量:
//削减系数,模拟摩擦力
float damping = 0.9;
这个变量的作用是为了模拟摩擦力和空气阻力的效果,如果没有这个变量,或者这个变量为1,那么这个运动将不会停止,这不符合我们对现实生活中运动的认知。在Circle类的update函数中,我们将速度向量乘上这个系数:
void update() {
...
velocity.mult(damping);
...
}
在主程序中,我定义了两个ArrayList,分别用来存储Circle类变量和Spring类变量:
ArrayList circles=new ArrayList();
ArrayList springs=new ArrayList();
然后在setup函数里编写了如下代码:
Circle Circle1 = new Circle(width/2, height/2);
Circle Circle2 = new Circle(width/2+50, height/2+50);
circles.add(Circle1);
circles.add(Circle2);
Spring Spring = new Spring(circles.get(0), circles.get(1),200);
springs.add(Spring);
简单来说就是两个Circle连接了一个弹簧,很好懂,这就是面向对象编程思想的优点。随后再进行一些力的应用,添加了鼠标拖拽事件,就可以跑了,我们看看效果:
其实一开始的效果不是那么理想,然后我对一些参数进行了调整,比如弹性系数k,削减系数damping 等,最后达成了很“Q弹”的效果。
然后我觉得两个球一根弹簧过于单调了,于是做了多个球,以及每个球都会与除自己之外的所有球连接一根弹簧。这样一来就会产生一个很神奇的效果,不管怎么拖拽,最终很可能会回到一个稳定的状态,比如五个的情况:
看起来就像一个魔法阵一样,如果用图论的知识来说,这是一个完全图。
最后,我添加了鼠标点击增加点的效果,这个和之前第0章做的相似:
void mouseClicked()
{
Circle newCircle = new Circle(mouseX, mouseY);
for(int i=0;i以及添加了渐变轨迹的效果:
fill(255,255,255,50);
rect(0,0,width,height);
最终效果如下:
最后附上所有代码。
Circle类:
class Circle {
PVector position;
PVector velocity;
PVector acceleration;
float mass = 5;
//削减系数,模拟摩擦力
float damping = 0.9;
PVector dragOffset;//拉动的距离向量
boolean dragging = false; // 鼠标是否按下
Circle(float x, float y) {
position = new PVector(x,y);
velocity = new PVector();
acceleration = new PVector();
dragOffset = new PVector();
}
void update() {
velocity.add(acceleration);
velocity.mult(damping);
position.add(velocity);
acceleration.mult(0);
}
void applyForce(PVector force) {
PVector f = force.get();//牛顿第二定律F=ma
f.div(mass);
acceleration.add(f);
}
void display() {
stroke(0);
strokeWeight(2);
fill(#98FFCC);
if (dragging) {
fill(#FF9898);
}
ellipse(position.x,position.y,mass*5,mass*5);
}
void clicked(int mx, int my) {
float d = dist(mx,my,position.x,position.y);
if (d < mass) {
dragging = true;
dragOffset.x = position.x-mx;
dragOffset.y = position.y-my;
}
}
void stopDragging() {
dragging = false;
}
void drag(int mx, int my) {
if (dragging) {
position.x = mx + dragOffset.x;
position.y = my + dragOffset.y;
}
}
}
Spring类:
class Spring {
PVector anchor; // 起始位置
float len;// 静止长度
float k = 0.05;//弹性系数
Circle a;
Circle b;
Spring(Circle a_, Circle b_, int l) {
a = a_;
b = b_;
len = l;
}
// 计算弹力
void update() {
PVector force = PVector.sub(a.position, b.position);//矢量指向从a点到b点
float d = force.mag();//计算向量长度
float stretch = d - len;//形变长度
force.normalize();
force.mult(-1 * k * stretch); //F=-kx
a.applyForce(force);
force.mult(-1);//牛顿第三定律
b.applyForce(force);
}
void display() {
strokeWeight(2);
stroke(0);
line(a.position.x, a.position.y, b.position.x, b.position.y);
}
}
主程序类:
//Circle[] circle = new Circle[5];
//Spring[] springs = new Spring[20];
ArrayList circles=new ArrayList();
ArrayList springs=new ArrayList();
void setup() {
size(600, 600);
for (int i = 0; i < 5; i++) {
Circle newCircle = new Circle(width/2+i*100-200, height/2+i*100-200);
circles.add(newCircle);
}
for (int i = 0; i < circles.size(); i++) {
for (int j = 0; j< circles.size(); j++) {
if(i!=j) {
Spring newSpring = new Spring(circles.get(i), circles.get(j),200);
springs.add(newSpring);
}
}
}
//Circle Circle1 = new Circle(width/2, height/2);
//Circle Circle2 = new Circle(width/2+50, height/2+50);
//circles.add(Circle1);
//circles.add(Circle2);
//Spring Spring = new Spring(circles.get(0), circles.get(1),200);
//springs.add(Spring);
}
void draw() {
fill(255,255,255,50);
rect(0,0,width,height);
for (Spring s : springs) {
s.update();
s.display();
}
for (Circle b : circles) {
b.update();
b.display();
b.drag(mouseX, mouseY);
}
}
void mouseClicked()
{
Circle newCircle = new Circle(mouseX, mouseY);
for(int i=0;i 总结
本文介绍了《代码本色:用编程模拟自然系统》第3章的主要内容,并在示例的基础上进行了拓展性的创作,创作了弹簧的模型并进行了拓展。