排序是算法里面一个老生常态的内容,基本是所有算法的第一关。
插入排序
算法思路
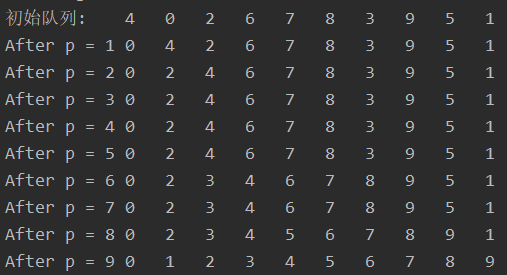
最简单的排序莫过于插入排序,需要N-1步,插入排序保证每个步骤0到p是有序的:
代码实现
public static > void insertSort(AnyType [] a) {
int j = 0;
for(int p = 1; p < a.length; p++) {
AnyType tmp = a[p];
for(j=p; j > 0 && tmp.compareTo(a[j - 1]) < 0; j--) {
a[j] = a[j-1];
}
a[j] = tmp;
System.out.print("After p = " + p);
System.out.print("\t");
for(AnyType num : a) {
System.out.print(num);
System.out.print('\t');
}
System.out.println();
}
}
时间复杂度
O(n2)
希尔排序
算法思路
希尔排序是根据他的创造人命名的(Donald Shell),它是第一种打破二次方时间复杂度的算法。我们通常选用N / 2并且逐步递减的方式来分序列的排序。
代码实现
public static > void shellSort(AnyType [] a) {
int j;
for(int gap = a.length / 2; gap > 0; gap /= 2) {
for(int i = gap; i < a.length; i++) {
AnyType tmp = a[i];
for(j = i; j>=gap && tmp.compareTo(a[j - gap]) < 0; j -= gap) {
a[j] = a[j - gap];
}
a[j] = tmp;
}
}
}
堆排序
算法思路
堆排序则是使用堆的数据结构来实现排序,可以在O(NlogN)复杂度完成。创建一个堆需要O(N)复杂度,然后通过不断的删除最小元素,将他们放在第二个数组中需要O(logN)复杂度。
但是这样的话需要更多的存储空间,同时消耗的内存也会增加。我们可以在每次删除最小元素后,滑动数组1个位置来避免新的数组的创建。
代码实现
public static int leftChild(int i) {
return i * 2 + 1;
}
private static > void percDown(AnyType[] a, int i, int n) {
int child;
AnyType tmp;
for(tmp = a[i]; leftChild(i) < n; i = child) {
child = leftChild(i);
if(child != n - 1 && a[child].compareTo(a[child + 1]) < 0) {
child++;
}
if(tmp.compareTo(a[child]) < 0) {
a[i] = a[child];
} else {
break;
}
}
a[i] = tmp;
}
public static void swapReferences(AnyType[] a, int index1, int index2) {
AnyType tmp = a[index1];
a[index1] = a[index2];
a[index2] = tmp;
}
public static > void heapsort(AnyType[] a) {
for(int i = a.length / 2 - 1; i >= 0; i--) {
percDown(a, i, a.length);
}
for( int i = a.length - 1; i > 0; i--) {
swapReferences(a, 0, i);
percDown(a, 0, i);
}
}
归并排序
算法思路
归并排序能保证最坏复杂度是O(NlogN),它是将两个已排序好的序列合并到一起。可以通过输入数组A、B产生一个输出数组C。通过简单的比较A、B的大小,并将剩余数组复制到输出数组中。
显而易见,归并排序需要N-1次的比较,如果N=1,那么只有一个元素也就是排序完成,然后归并左半部分和右半部分。这种算法是比较典型的分治策略,这个问题并分为若干小问题然后递归的解决它。
代码实现
private static > void mergeSort(AnyType[] a, AnyType[] tmpArray, int left, int right) {
if (left < right) {
int center = (left + right) / 2;
mergeSort(a, tmpArray, left, center);
mergeSort(a, tmpArray, center + 1, right);
merge(a, tmpArray, left, center + 1, right);
}
}
public static > void mergeSort(AnyType[] a) {
AnyType[] tmpArray = (AnyType[]) new Comparable[a.length];
mergeSort(a, tmpArray, 0, a.length - 1);
}
private static > void merge(AnyType[] a, AnyType[] tmpArray, int leftPos,
int rightPos, int rightEnd) {
int leftEnd = rightPos - 1;
int tmpPos = leftPos;
int numElements = rightEnd - leftPos + 1;
while (leftPos <= leftEnd && rightPos <= rightEnd) {
if (a[leftPos].compareTo(a[rightPos]) <= 0) {
tmpArray[tmpPos++] = a[leftPos++];
} else {
tmpArray[tmpPos++] = a[rightPos++];
}
}
while (leftPos <= leftEnd) {
tmpArray[tmpPos++] = a[leftPos++];
}
while (rightPos <= rightEnd) {
tmpArray[tmpPos++] = a[rightPos++];
}
for (int i = 0; i < numElements; i++, rightEnd--) {
a[rightEnd] = tmpArray[rightEnd];
}
}
快速排序
算法思路
正如其名,快速排序是一种非常快速的排序算法,它的平均时间复杂度为O(NlogN)。通过高度的内部循环优化,它可以非常高效。它的最坏时间复杂度为O(N2),但通过一些简单的优化就可以极大的避免这种情况的发生。
快速排序很容易被理解,类似于归并排序,快速排序也是一种分治策略。我们可以先来一种简单的方式,任意选择一个元素,然后将它分为三个部分,小于、等于、大于。然后递归的排序第一组和第三组。最后再将他们组合在一起,代码也非常好写
public static void sort(List items) {
if(items.size() > 1) {
List smaller = new ArrayList<>();
List same = new ArrayList<>();
List larger = new ArrayList<>();
Integer chosenItem = items.get(items.size() / 2);
for(Integer i : items) {
if(i < chosenItem) {
smaller.add(i);
} else if(i > chosenItem) {
larger.add(i);
} else {
same.add(i)
}
}
sort(smaller);
sort(larger);
items.clear();
items.addAll(smaller);
items.addAll(same);
items.addAll(larger);
}
}
但申请了额外的序列,递归的排序我们感觉这和归并排序差不多,我们需要避免使用额外的内存。
更为经典的快速排序可以这样实现,如果数组S有0或者1个元素直接返回。否则,选一个元素v,我们称它为枢纽。然后将S分成两个不相交的子集小于等于v和大于v,然后在各自的子序列中重复。
理想中,我们希望相等数量的key落在两个分组中。
通常,我们喜欢选择第一个元素作为枢纽,然而当数组已经是有序的时候,我们的时间复杂度会来到指数级。一种安全的方法是随机的选择这个枢纽,但计算机中的随机却不是那么简单。中位数表示数组中第N/2个大的数,它非常适合用来做枢纽,但是获得数组的中位数并不是一件简单的事情,因此我们通常会随机取3个数,然后用他们的中位数来代替。实践中,我们可以选择头尾和中间,然后从这三个数中选择中位数来作为枢纽。
public static > void quicksort(AnyType[] a) {
quicksort(a, 0, a.length - 1);
}
private static > AnyType median3(AnyType[] a, int left, int right) {
int center = (left + right) / 2;
if(a[center].compareTo(a[left]) < 0) {
swapReferences(a, left, center);
}
if(a[right].compareTo(a[left]) < 0) {
swapReferences(a, left, right);
}
if(a[right].compareTo(a[center]) < 0) {
swapReferences(a, center, right);
}
swapReferences(a, center, right - 1);
return a[right - 1];
}
private static > void quicksort(AnyType[] a, int left, int right) {
if(left <= right) {
AnyType pivot = median3(a, left, right);
int i = left;
int j = right - 1;
for(;;) {
while (a[i].compareTo(pivot) < 0) {
i++;
}
while (a[j].compareTo(pivot) > 0) {
j--;
}
if(i < j) {
swapReferences(a, i, j);
} else {
break;
}
}
swapReferences(a, i, right - 1);
quicksort(a, left, i - 1);
quicksort(a, i + 1, right);
}
}