数组斐波那契数列，排序15种 splice() concat()在JavaScript 和 TypeScript 语法基础 数组，字符串的split()文章中详细解释

---

快速排序

排序

1.0 十大经典排序算法：https://www.runoob.com/w3cnote/ten-sorting-algorithm.html

---

** ******************* 1冒泡排序： ********************************

int[] num = new int[]{ 19,12,34,45,65,12,33,432};
for(int i = 0 ; i < num.Length - 1 ; i++){
for(int j=0 ; j < num.Length-1- i ; j++){//每次 i 把 (num.Length-1- i)中的最大一位大泡冒出来放到最后，第二次就不用在比上次的最大的了，所以就少了num.Length-1- i中的最后i个元素
if(num[j]> num[j+1])
{
int a=num[j];
num[j]=num[j+1];
num[j+1]=a;
}
}
}
//使用 foreach对数组进行遍历，然后使用console输出数组。
foreach(int number in num){
Console.WriteLine(number);}
时间花销为：[ n(n-1) ] / 2 = x 既约等于n^2 不用在意具体数字；所以最优的情况时间复杂度为：平均O( n^2 )；
空间复杂度：最差的空间复杂度就是开始元素逆序排序，每次都要借用一次内存，按照实际的循环次数，平均空间复杂度为O(1)
最优的空间复杂度，同样，就是不需要借用第三方内存空间，则复杂度为0
最差的空间复杂度就是开始元素逆序排序，每次都要借用一次内存，按照实际的循环次数，为O(N)
平均的空间负杂度为：O（1）

********************* 2选择排序 ********************* 类似于守擂台，后面的人挨个挑战

static void Main(string [] args){
int[] group = {4,1,7,8,12,3,5};
int temp;
int pos = 0;
for(int i = 0;i < group.Length - 1 ; i++){
pos = i;
for(int j = i +1 ; j < group.Length; j++){//每一个都与后面的所有比较，把最小的复制到最前面 //每次大遍历的 i 遍历一次，都把gouup[j]中的最小值放到最前面的group[i]s上。
if(group[pos] > group[ j ]){//每次的group[i]都跟后面的每个group[j]比较
pos = j;
}
}
temp = group[i]; //每次i++，才把 j 到 n中的数找出一个最小的，才进行值的替换，
group[ i ] = group[pos];
group[pos] = temp;

}

}

********************* 插入排序 *********************

类似于 冒泡 和 快速排序的结合
for(i)循环把第一个提出来 与for[j]循环的每一个比较，比较成功过了 再交换数据

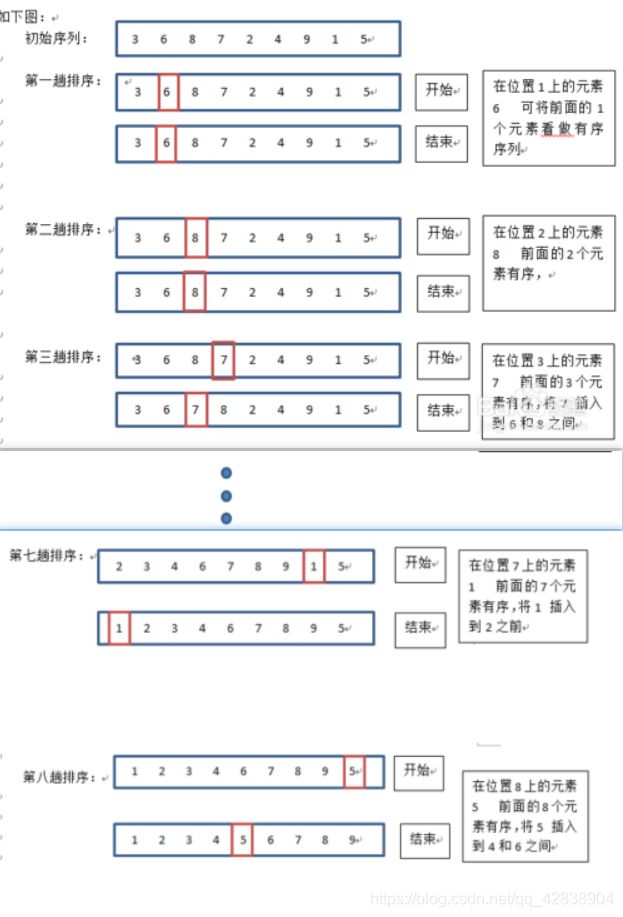
升序就用例1： 插入法 排序主要是 for(i)的变化 j只是for(i - 1)前面所有的比较
例2：
include
main()
{
int []array = new int[]{3,6,8,7,2,4,9,1,5,10},
int i,j,temp;
for(i=1;i < array.length;i++) /外循环控制趟数，n个数从第2个数开始到最后共 进行n-1次插入/
{
temp= array [i]; /将待插入数暂存于变量t中/，当i=1,就是把a[1]第二位数放到t中
for( j = i-1 ; j >= 0 ; j-- ) /在有序序列（下标0 ~ i-1）中寻找插入位置/
{
if(temp< array[j])
{
array [ j + 1] = array [j]; /若未找到插入位置，则当前元素后移一个位置/
array [ j ] = temp; /找到插入位置，完成插入/
}
}

	}
	printf("The sorted numbers: ");
	for(i=0 ; i < array.length ; i++)
	printf("%d ",array[i]);
	printf("\n");

}
时间花销为：[ n(n-1) ] / 2；所以最优的情况时间复杂度为：O( n^2 )；
空间复杂度：最差的空间复杂度就是开始元素逆序排序，每次都要借用一次内存，按照实际的循环次数，为O(1)
**
用插入排序法对10个整数进行降序排序。
降序就用 例2：** 插入法 排序主要是 for(i)的变化 j只是for(i - 1)前面所有的比较
例1：
include
main()
{
int []array = new int[]{3,6,8,7,2,4,9,1,5,10},
int i,j,temp;
for(i=1;i 外循环控制趟数，n个数从第2个数开始到最后共 进行n-1次插入/
{
temp = array[i]; /将待插入数暂存于变量t中/，当i=1,就是把a[1]第二位数放到t中
for( j = i-1 ; j >= 0 ; j-- ) /* 遍历已经排序好了的部分 如果比arr[i],就把arr[i]的值移动到下一位得空间内，然后把temp插入到这个位置 在有序序列
（下标0 ~ i-1）=中寻找插入位置*/
{
if(temp> array[j])
{
array [ j + 1] = array [j]; /若未找到插入位置，则当前元素后移一个位置/
array [ j ] = temp ; /找到插入位置，完成插入/
}
}

	}
	printf("The sorted numbers: ");
	for(i=0 ; i < array.length ; i++)
	printf("%d ",array[i]);
	printf("\n");

}

//

五. 快速排序(Quicksort)

基本思想：（分治）
先从数列中取出中心轴key值；
将比这个数小的数全部放在它的左边，大于或等于它的数全部放在它的右边；
对左右两个子序列重复第二步，直至各区间只有1个数。
辅助理解：挖坑填数
初始时 i = 0; j = 9; key=72
由于已经将a[0]中的数保存到key中，可以理解成在数组a[0]上挖了个坑，可以将其它数据填充到这来。
从j开始向前找一个比key小的数。当j=8，符合条件，a[0] = a[8] ; i++ ; 将a[8]挖出再填到上一个坑a[0]中。
这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办了？简单，再找数字来填a[8]这个坑。
这次从i开始向后找一个大于key的数，当i=3，符合条件，a[8] = a[3] ; j-- ; 将a[3]挖出再填到上一个坑中。
数组：72 6 57 88 60 42 83 73 48 85
0 1 2 3 4 5 6 7 8 9
此时 i = 3; j = 7; key=72
再重复上面的步骤，先从后向前找，再从前向后找。
从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++;
从i开始向后找，当i=5时，由于i==j退出。
此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将key填入a[5]。
数组：48 - 6 - 57 - 88 - 60 - 42 - 83 - 73 - 88 - 85
0 1 2 3 4 5 6 7 8 9
可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。
<数组：48 - 6 - 57 - 42 - 60 - 72 - 83 - 73 - 88 - 85
0 1 2 3 4 5 6 7 8 9
平均时间复杂度：O(N*logN)
代码实现：
实例
public static void quickSort(int a[],int l,int r){
if(l>=r)//L>=R时就退出
return;
int i = l; int j = r; int key = a[l];//选择第一个数为key
while(i while(i=key)//从右向左找第一个小于key的值
j–;
if(i a[i] = a[j];
i++;
}
while(i i++;
if(i a[j] = a[i];
j–;
}
}
//i == j
a[i] = key;
quickSort(a, l, i-1);//递归调用 左子序列的长度从 l(L) 到 i-1 每次key = a[i] 的中心轴不固定是在哪里
quickSort(a, i+1, r);//递归调用 右子序列的长度是从 i+1 到 r （l (L)和 r 是有每个子序列决定）
}
第一次调用 初始时 i = l= 0; j = r= 9; key = a[0]=72
key值的选取可以有多种形式，例如中间数或者随机数，分别会对算法的复杂度产生不同的影响。

splice（）方法采坑
splice()方法用于插入、删除或者替换数组里的元素，在做项目时，我们会经常用到这种方法。这种方法会改变原数组！
来看看语法：
它的主要参数有index，howmany，item1，…，itemX；
index——必须。规定从何处添加/删除元素，表示下标。
howmany——必须。规定删除多少元素，必须是数字，但可以是0；
item1，…，itemX——可选。要添加到数组的新元素。

function myFunction(){
		var arr = ["one","two","three","four","five","six"];
		arr.splice(2,1,"一","二");
		var x = document.getElementById("text");
		x.innerHTML = arr;
	}

结果：one,two,一，二，,four,five,six

或者咱们也可以直接删除：
function myFunction(){
var arr = [“one”,“two”,“three”,“four”,“five”,“six”];
arr.splice(2,2);
var x = document.getElementById(“text”);
x.innerHTML = arr;
}
结果：one,two,five,six

//二分查找

时间复杂度：log n
总共有n个元素，每次查找的区间大小就是n，n/2，n/4，…，n/2^k（接下来操作元素的剩余个数），其中k就是循环的次数。
由于n/2^k取整后>=1，
即令n/2^k=1，
可得k=log2n,（是以2为底，n的对数），所以时间复杂度可以表示O()=O(logn)
空间复杂度： O(N) 所以空间复杂度是： O(N) （ 递归一次要开辟一个空间）
**
///
/// 二分法查找
///
///
/// 要查找的对象
public static int BinarySearch(int[] arr,int value)
{
int left= 1;
int right= arr.Length;
while(left <= right)
{
int mid= (left+ right) / 2;
if (value == arr[mid])
{
return mid;//如果找到了就直接返回这个元素的索引
}
else if(value >arr[mid])
{
left= mid + 1;
}
else
{
right= mid - 1;
}
}
return -1;//如果找不到就返回-1；
}

//二分查找算法 数组
int BinarySearch(List Tbi, ElementType K)
{//在表 Tbi 中查找关键字为 K 的数据元素
int left, right, mid, NoFound = -1;
left = 1; //初始左边界
right = Tbi->Length; //初始右边界
while (left <= right)
{
mid = (left + right)/2; //计算中间元素坐标 左右值加相加/2 能辅助int 向下取整时正好取到中间值
if (K < Tbi->Element[mid]) right = mid - 1; //调整右边界
else if (K > Tbi->Element[mid]) left = mid + 1; //调整左边界
else return mid; //查找成功，返回数据元素的下标
}
return NoFound; //查找不成功，返回 -1
}

斐波那契（黄金比例）查找

***：按斐波那契数列的值当数组下标进行 类似二分查找
时间复杂度，O(2 ^N) 我们只看最坏情况，最坏情况是这个二叉树是满的，若是满的，则有2^(N-1) - 1，所以时间复杂度是O(2 ^N)。
空间复杂度 O(N)。 fib（6）的的=最深高度是5，所以空间复杂度是O(N-1)，即O(N)。
**

顺序查找：按数组下标顺序依次查找
**

插值查找：

**
直接插入排序是稳定的,它的
时间复杂度为__ O(n^2)__,
空间复杂度为_ O(1) (指在原数据以外的辅助空间)_

---

散列表（哈希表）查找**

：

时间复杂度O(N)，//n个数就调用n次 哈希函数查找
空间复杂度O(1) //每次开辟了一个内存空间
哈希函数可以自己定义：直接定制法

取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B 线性函数
优点：简单、均匀
缺点：需要事先知道关键字的分布情况
适合查找比较小且连续的情况
面试题：找出一个字符串中第一个只出现一次的字符，要求：时间复杂度O(N)，空间复杂度O(1)

**除留余数法：**设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数：Hash(key) = key % p(p<=m),将关键码转换成哈希地址
折叠法
数学分析法
随机数法
平方取中法

---

斐波那契数列

---

例1：
long int f1,f2; /定义f1、f2为长整形/
int i; /定义整型变量i/
f1=1;f2=1; /给f1、f2赋初值为1/
for(i=1;i<=20;i++)
{
printf("%12ld\n%12ld\n",f1,f2); /输出斐波那契数列/
f1=f1+f2; /数列中从第3项开始每一项等于前两项之和/
f2=f2+f1;
}
例2：
long long Fib(int n)
{
assert(n >= 0);
return n<2 ? n : Fib(n - 1) + Fib(n-2);
}

递归算法实现

CShape实现
namespace ConsoleApp1
{
class Program
{
static void Main(string[] args)
{
int a = 0, b = 1, c = 1;
Console.WriteLine(“请输入一个数：”);//输入的数赋值给n
int n = int.Parse(Console.ReadLine()) ;
for (int i = 3; i <= n; i++)
{
a = b;
b = c; //3个数中把前两位的值赋值给后两位的值
c = a + b;
}
Console.WriteLine©; //输出最终结果
Console.ReadKey();
}
}
}

递归算法实现

include

using namespace std;
int f(int n)
{
if(n0) return 0;
if(n1) return 1;
if(n>=2)
{
return f(n-1)+f(n-2);
}
}
int main()
{
int n;
cin>>n;
cout< return 0;
}

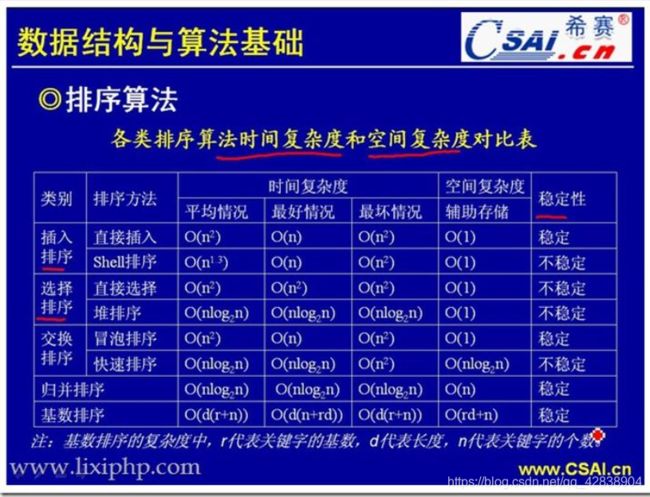
或则表https://www.iteye.com/blog/lvdccyb-2064769供参考

基本概念

比较排序和非比较排序：

常见的排序算法都是比较排序

比较排序的时间复杂度通常为 O(n2) 或者 O(nlogn)，比较排序的时间复杂度下界就是 O(nlogn)
非比较排序包括计数排序、桶排序和基数排序，非比较排序对数据有要求，因为数据本身包含了定位特征，所有才能不通过比较来确定元素的位置

非比较排序的时间复杂度可以达到 O(n)，但是都需要额外的空间开销
几种排序算法的总结与比较
排序方法 平均时间 最坏时间 辅助空间 稳定性
简单排序 - 冒泡排序 O(n2) O(n^2) O(1) 稳定
简单排序 - 选择排序 O(n2) O(n2) O(1) 不稳定
简单排序 - 插入排序 O(n2) O(n2) O(1) 稳定
快速排序 O(nlogn) O(n2) O(logn) 不稳定
堆排序 O(nlogn) O(nlogn) O(1) 不稳定
归并排序 O(nlogn) O(nlogn) O(n) 稳定
希尔排序 O(nlogn2) = O(n1.3) O(n2) O(n) 不稳定
计数排序 O(n + k) O(n + k) O(k) 稳定
桶排序 O(n + k) O(n2) O(n) 稳定
基数排序 O(nk) O(nk) O(n + k) 不稳定
Array Sorting Algorithms
冒泡排序
通过与相邻元素的比较和交换来把小的数交换到最前面，或者把大的数交换到最后面。

冒泡排序的时间复杂度为 O(n2)。

代码如下：

// 冒泡排序
public void bubbleSort(int[] nums) {
    if (nums == null || nums.length == 0)
        return;

    // 只需要循环 n-1 次
    for (int i = 0; i < nums.length - 1; i++) {
        for (int j = 0; j < nums.length - i - 1; j++) {
            if (nums[j] > nums[j + 1]) {
                swap(nums, j, j + 1);
            }
        }
    }
}

分析：假设输入为 4, 2, 5, 1, 3
第一次循环后，变为 2, 4, 1, 3, 5，5 被移动到最后
第二次循环后，变为 2, 1, 3, 4, 5，4 被移动到最后的第二个位置
以此类推

选择排序
选择排序的思想其实和冒泡排序有点类似，都是在一次排序后把最小的元素放到最前面。
但是过程不同，冒泡排序是通过相邻的比较和交换。而选择排序是通过对整体的选择。

其实选择排序可以看成冒泡排序的优化，因为其目的相同，只是选择排序只有在确定了最小数的前提下才进行交换，大大减少了交换的次数。

选择排序的时间复杂度为 O(n2)。

代码如下：

// 选择排序
public void selectSort(int[] nums) {
    if (nums == null || nums.length == 0)
        return;

    int minIndex;

    // 只需要循环 n-1 次
    for (int i = 0; i < nums.length - 1; i++) {
        minIndex = i;

        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] < nums[minIndex]) {
                minIndex = j;
            }
        }

        if (minIndex != i) {
            swap(nums, i, minIndex);
        }
    }
}

分析：假设输入为 4, 2, 5, 1, 3
第一次循环后，变为 1, 2, 5, 4, 3，1 被移动到最前
第二次循环后，变为 1, 2, 5, 4, 3，2 被移动到最前的第二个位置
以此类推

插入排序
插入排序不是通过交换位置而是通过 比较找到合适的位置插入元素来达到排序的目的。
插入排序的时间复杂度为 O(n2)。
代码如下：
// 插入排序
public void insertSort(int[] nums) {
if (nums == null || nums.length == 0)
return;
// 假设第一个数位置是正确的
for (int i = 1; i < nums.length; i++) {
int j = i;
int target = nums[j];
// 后移
while (j > 0 && nums[j - 1] > target) {
nums[j] = nums[j - 1];
j–;
}
// 插入
nums[j] = target;
}
}
分析：假设输入为 4, 2, 5, 1, 3
第一次循环后，变为 2, 4, 5, 1, 3
第二次循环后，变为 2, 4, 5, 1, 3
第三次循环后，变为 1, 2, 4, 5, 3
以此类推

快速排序
其实其思想是来自冒泡排序，冒泡排序是通过相邻元素的比较和交换把最小的冒泡到最顶端，而快速排序是比较和交换小数和大数，这样一来不仅把小数冒泡到上面同时也把大数沉到下面。
快速排序是不稳定的，其时间复杂度为 O(nlogn)。
代码如下：

// 快速排序
public void quickSort(int[] nums, int start, int end) {
    if (start >= end)
        return;
    int partitionIdx = partition(nums, start, end);
    quickSort(nums, start, partitionIdx - 1);
    quickSort(nums, partitionIdx + 1, end);
}
// partition
public int partition(int[] nums, int start, int end) {
    if (start == end) {
        return start;
    }
    int pivot = nums[start];
    while (start < end) {
        // 从右往左找到第一个小于 pivot 的元素
        while (start < end && nums[end] >= pivot) {
            end--;
        }
        // 把小的移动到左边
        nums[start] = nums[end];
        // 从左往右找到第一个大于 pivot 的元素
        while (start < end && nums[start] <= pivot) {
            start++;
        }
        // 把大的移动到右边
        nums[end] = nums[start];
    }
    // 最后把pivot赋值到中间
    nums[start] = pivot;
    return start;
}

分析：假设输入为 4, 2, 5, 1, 3
第一轮递归后，变为 3, 2, 1, 4, 5
第一轮递归后，变为 1, 2, 3, 4, 5
以此类推

堆排序
堆排序是借助堆来实现的选择排序。
注意：如果想升序排序就使用大顶堆，反之使用小顶堆。原因是堆顶元素需要交换到序列尾部。

具体参见：堆的使用及相关LeetCode题目

归并排序
归并排序使用了递归分治的思想。
把待排序列看成由两个有序的子序列，然后合并两个子序列，然后把子序列看成由两个有序序列…倒着来看，其实就是先两两合并，然后四四合并…最终形成有序序列。

归并排序空间复杂度为 O(n)，时间复杂度为 O(nlogn)。

代码如下：

// 归并排序
public void mergeSort(int[] arr, int start, int end) {
    if (start >= end)
        return;

    int mid = (start + end) / 2;

    // 递归排序左边
    mergeSort(arr, start, mid);
    // 递归排序右边
    mergeSort(arr, mid + 1, end);

    // 合并
    merge(arr, start, mid, end);
}

// 合并两个有序数组
public void merge(int[] arr, int start, int mid, int end) {
    int[] temp = new int[end - start + 1]; // 中间数组

    int i = start;
    int j = mid + 1;
    int k = 0;
    while (i <= mid && j <= end) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }

    while (i <= mid) {
        temp[k++] = arr[i++];
    }

    while (j <= end) {
        temp[k++] = arr[j++];
    }

    for (int p = 0; p < temp.length; p++) {
        arr[start + p] = temp[p];
    }
}

希尔排序
希尔排序是插入排序的一种高效率的实现。
简单的插入排序中，如果待排序列是正序时，时间复杂度是O(n)，如果序列是基本有序的，使用直接插入排序效率就非常高。
希尔排序就利用了这个特点。基本思想是：先将整个待排记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录基本有序时再对全体记录进行一次直接插入排序。

希尔排序时间复杂度为 O(nlogn)。

代码如下：

// 希尔排序的一趟插入
public void shellInsert(int[] nums, int d) {
    for (int i = d; i < nums.length; i++) {
        int j = i - d;
        
        // 记录要插入的数据
        int temp = nums[i];
        // 从后向前，找到比其小的数的位置
        while (j >= 0 && nums[j] > temp) {
            // 向后挪动
            nums[j + d] = nums[j];
            j -= d;
        }

        // 存在比其小的数
        if (j != i - d)
            nums[j + d] = temp;
    }
}

// 希尔排序
public void shellSort(int[] nums) {
    if (nums == null || nums.length == 0)
        return;

    int d = nums.length / 2;
    while (d >= 1) {
        shellInsert(nums, d);
        d /= 2;
    }
}

计数排序
前提条件：待排序的数要满足一定的范围的整数，而且计数排序需要比较多的辅助空间。其基本思想是，用待排序的数作为计数数组的下标，统计每个数字的个数。然后依次输出即可得到有序序列。

计数排序空间复杂度为 O(n)，时间复杂度为 O(n)。

代码如下：

// 计数排序
public void countSort(int[] nums) {
    if (nums == null || nums.length == 0)
        return;

    int max = max(nums);

    int[] counts = new int[max + 1];
    Arrays.fill(counts, 0);

    // 计数
    for (int i : nums) {
        counts[i]++;
    }

    int k = 0;
    for (int i = 0; i <= max; i++) {
        for (int j = 0; j < counts[i]; j++) {
            nums[k++] = i;
        }
    }
}

public int max(int[] nums) {
    int max = Integer.MIN_VALUE;
    for (int i : nums) {
        if (i > max)
            max = i;
    }

    return max;
}

桶排序
桶排序算是计数排序的一种改进和推广。
基本思想：使用映射函数将待排序的数组划分成M个的子区间(桶) 。接着对每个桶中的所有元素进行比较排序(可以使用快排)。然后依次枚举输出每个桶中的全部内容即是一个有序序列。
桶排序之所以能够高效，其关键在于这个映射函数，它必须做到：如果关键字k1

代码如下：

// 桶排序
public void bucketSort(int[] nums) {
    if (nums == null || nums.length == 0)
        return;

    int max = Integer.MIN_VALUE;
    int min = Integer.MAX_VALUE;
    for (int i = 0; i < nums.length; i++) {
        max = Math.max(max, nums[i]);
        min = Math.min(min, nums[i]);
    }

    // 桶数
    int bucketNum = (max - min) / nums.length + 1;

    // 创建桶
    ArrayList> buckets = new ArrayList>(
            bucketNum);
    for (int i = 0; i < bucketNum; i++) {
        buckets.add(new ArrayList());
    }

    // 将每个元素放入桶
    for (int i = 0; i < nums.length; i++) {
        int idx = (nums[i] - min) / (nums.length);
        buckets.get(idx).add(nums[i]);
    }

    // 对每个桶进行排序
    for (int i = 0; i < buckets.size(); i++) {
        Collections.sort(buckets.get(i));
    }

    // 还原排好序的数组
    int k = 0;
    for (List bucket : buckets) {
        for (int i : bucket) {
            nums[k++] = i;
        }
    }
}

基数排序
基数排序是一种和前面排序方式不同的排序方式，基数排序不需要进行关键字之间的比较。
基数排序是一种借助多关键字排序思想对单逻辑关键字进行排序的方法。所谓的多关键字排序就是有多个优先级不同的关键字。
如果对数字进行排序，那么个位、十位、百位就是不同优先级的关键字，如果要进行升序排序，那么个位、十位、百位优先级依次增加。

代码如下：

// 基数排序
public void radixSort(int[] nums) {
    if (nums == null || nums.length == 0)
        return;

    // 获取最大位数
    int maxBit = getMaxBit(nums);

    /*
     * 先根据个位数排序，再根据十位数排序...
     */
    for (int i = 1; i <= maxBit; i++) {
        // 分配
        List> buf = distribute(nums, i);

        // 收集
        collect(nums, buf);
    }

}

// 分配
public List> distribute(int[] nums, int iBit) {
    List> buf = new ArrayList>();
    for (int j = 0; j < 10; j++) {
        buf.add(new LinkedList());
    }

    for (int i = 0; i < nums.length; i++) {
        buf.get(getNBit(nums[i], iBit)).add(nums[i]);
    }

    return buf;
}

// 收集
public void collect(int[] arr, List> buf) {
    int k = 0;
    for (List bucket : buf) {
        for (int i : bucket) {
            arr[k++] = i;
        }
    }
}

// 获取最大位数
public int getMaxBit(int[] nums) {
    int max = Integer.MIN_VALUE;
    for (int i : nums) {
        max = Math.max(max, (i + "").length());
    }

    return max;
}

// 获取数字x的第n位
public static int getNBit(int x, int n) {
    String str = x + "";
    if (str.length() < n)
        return 0;
    else
        return str.charAt(str.length() - n) - '0';
}