【论文阅读】Triple GANs论文阅读

我的前言

翻译结合我自己想法啊，但是我贼菜的而且时间有限，所以，我都是简单的大致理解一下，然后翻译。发出来的原因，更多是想做个笔记。
翻译的乱七八糟的。。。这就是我现在的感受了

论文

论文作者

Chongxuan Li， Kun Xu, Jun Zhum, Bo Zhang
Tsinghua University
三位清华的大神

Abstract 概要

GANs （对抗生成神经网络）已经在图片生成和半监督学习上有不错的保证了。但是，目前的GANs在半监督学习上有两个问题。

1. 生成器和判别器（即分类器）可能不是同时最优的。
2. 生成器不能控制生成样本的语义

这个样本实质上是由于两个玩家的博弈制度。在这种制度下，一个判别式模型来分享一个不相容的角色，在识别一个假的样本并且预测标签，而且它只评估没有考虑标签的数据。

为了解决这个问题，我们提出一个三人对抗的生成网络。（Triple-GAN）。在这个模型中，包括有三个博弈参与者，分别是一个生成器，一个判别器，一个分类器。

• 这个生成器和分类器表现这个在图片和标签之间的条件分布。
• 这个判别器只（solely）专注于分辨假图片-标签对

我们设计了兼容的效用去保证这个分布被这两个收敛到数据分布的分类器和生成器表现出来。

我们在不同数据上实验的结果表明（demonstrate）Triple-GAN 作为一个统一的模型可以同时保证下面两点

• 达到了最先进的，最高端的，最前沿的分类通过深度生成模型的分类结果
• 解决了，在数据空间，类别和风格的平滑地导入和转化，通过在潜在的类别条件空间上的插值（interpolation）

附上这段的论文

Introduction 介绍

深度生成模型（DGMs）可以捕捉到数据的底层分布并生成新的样本。
最近，在生成实际图片上有了一个有重大意义的进展基于生成对抗网络（GANs）。生成对抗网络是制定了一个两个玩家的博弈。在这个博弈当中，生成器G把随机噪声Z作为输入，然后生成了样本G(z)在数据空间；而，判别器（Discriminator）D 识别一个给定的样本，来自于实际的数据分布P(x)，还是来自于生成器G。

G和D都是被参数化为深度神经网络，并且训练过程就是解决下面的这个最小值问题。

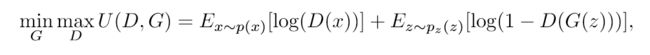
这里，$p_z(z)$是一个样本分布（例如：均匀分布（uniform）或者是正态分布（norm））。然后$U(\cdot )$表示一个结果。

给出一个生成器然后定义分布$p_g$，最优的判别式就是
$D(x)=p(x)/(p_g(x)+p(x)$ 在一个非参数化的设置中，然后这个博弈的均衡（equilibrium of the game）当且仅当 $p(x)=p_g(x)$的时候达到。就图像生成来言，这是理想的。

GANs和DGMs在一般情况下，已经被证明了在半监督学习（SSL）上的有效性，当保证了生成的能力。在同样的两个玩家的博弈模型中，Cat-GANs概括了GANs用一个分类判别的网络，并且一个目标函数是去极小化一个预测基于真实数据的条件熵，同时也要最大化，预测基于生成的样本的条件熵。

这有两个问题在GANs应用在半监督学习SSL上

1. 生成器和判别器（即分类器）可能不是同时最优的。
2. 生成器不能控制生成样本的语义

对于第一个问题，Salimans et al 提出两个可选的训练对象，效果在分类或者图像生成的半监督模型上都是还不错的，但不是同时都不错。

这个特征匹配在分类上非常不错，但是在生成不同的样本上，当另外一个损失函数 minibatch 判别函数，在实际的图像生成上表现的很好。

这个现象没有被深入地分析，并且，在这里，我们认为主要源自于 两个玩家的博弈机制，在这样的机制下，只有一个判别器去完成两个不兼容的内容–识别假的样本，并且预测真的样本。

特别地，我们人假设G是最优的，即 $p(x)=p_g(x)$ 并且考虑一个样本x来自于$p_g(x)$。一方面，作为一个判别器，最优的D应该能识别x是一个假的样本，有着非0概率。另一方面，作为一个分类器，这个最优的D应该总是预测这个正确的x的类别。

这就好像，D有两个不同的收敛点一样。表面G和D可能不是同时最优的。而且，给一个不是最优的G，这样的情况占大多数。给一个样板来自于重叠区域，那么两个在D中的角色任然会通过不同的处理这个样本完成，导致很糟糕的分类。

对于第二个问题，disentangling （解开）有意义的物理因子，像有限监督的潜在表征的对象分类。然而根据目前的知识来看，没有一个存在的GANs是可以学习一个解开的表征在半监督模型中，即使一些工作可以学习这样的表述被给出来全部的标签的。又一次的，我们认为这是来自两个玩家的对抗的模型。

为了解决这些问题，提出了Triple-GAN。（后面的翻不动了。。。）
直接跳到Methods部分好了，看看算法实现。

Method

我们考虑在学习一个DGMs在半监督的设置下，这里我们又部分标签好的数据集。

• x表示输入的数据
• y表示输出的标签

目标是去预测这个标签y给没有标签好的数据，同时也给生成出来的新样本x在基于y的条件下。
这是很不同于无监督设置的给纯粹的生成，在无监督的条件下，唯一的目标就是去生成一个样本x然后去欺骗判别器x。

因此两个人的博弈是可以满足去描述这个过程在GANs中的。

在我们的设置中，作为一个标签信息，y是不完整的（也是不确定的）。我们的密度模型应该是被表征在x和y的空间上。

因此，有一个联合分布 P(x,y)在输入的标签对上。

双人博弈的一个比较直接的应用，是不可行的，由这个缺失的y数据。

不像之前的工作，给两人博弈有一个限制，然后可以导致一个不相容的目标。我们建立了我们的博弈理论的对象，基于在这个联合分布上的观测。

表示出来就是，概率公式的条件公式（可以回去翻翻概率论的书）。

条件概率是针对于分类的过程的，和有分类的生成器。
为了去联合得到评价这个条件分布（被表征为一个分类器网络的模型和一个有类别条件的生成器网络），我们定义了一个单独的判别器，有一个特定的角色，就是去区分是否这个人样本是来自于实际数据，还是来自这模型。

因此，我们很自然的扩展GANs到Triple-GANs，这样的一个三人对抗的模型去表征分类的和有类别条件的生成模型。

3.1 三个玩家的博弈

Triple-GAN 包括有三个部分

1. 一个分类器C，近似地表征条件分布 $P_c(y|x)=p(y|x)$
2. 一个有类别条件的生成器G，禁止的表征为，一个条件分布的另外一个方向。$P_G(x|y)=p(x|y)$
3. 一个判别器D，区分一个数据对(x,y)来自于真实数据分布p(x,y)

所有的组成成员都被表示神经网络的参数成员。