机器人路径规划之Dijkstra算法

在机器人路径规划之动态窗口法文中，介绍了一种局部路径规划方法——动态窗口法，本文将介绍一种全局路径规划方法——Dijkstra算法(狄克斯特拉算法)。Dijkstra算法是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。

基本原理

其基本原理是：每次新扩展一个距离最短的点，更新与其相邻的点的距离。

以下图为例，计算左上角节点到右下角节点的最短路径，箭头上的数值表示两个节点间的距离

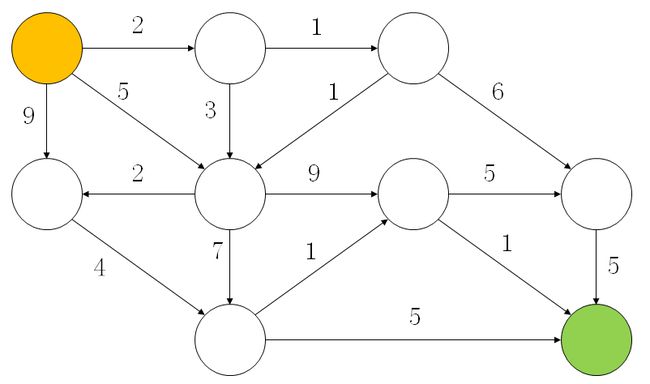
首先扩展第一个节点，计算其余节点与第一个节点的距离，如下图所示，用橙色标出已经扩展的节点，未扩展的节点仍用绿色标出，其中圆中的数值表示与第一个节点的距离，$\infty$表示该节点没有直接到达此时已扩展节点的路径。

从未扩展的节点（绿色部分）中选择距离最小的节点进行拓展，并更新其余节点到第一个节点的距离，如下图

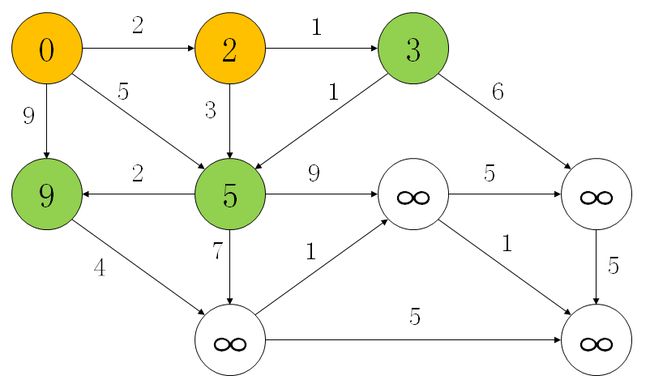
重复进行上面的步骤，直到所有节点都已扩展。

最后标出左上角节点到右下角节点的最短路径

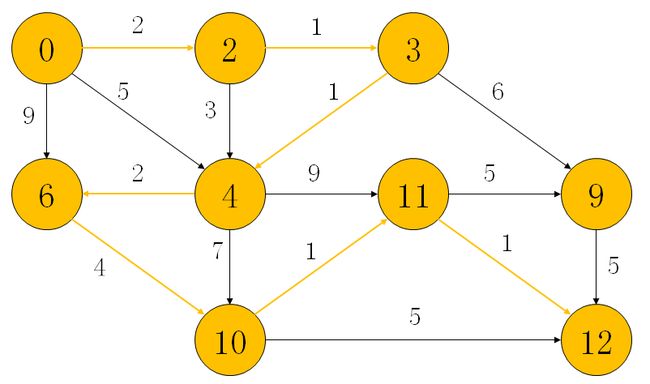
参考：https://wiki.mbalib.com/wiki/Dijkstra%E7%AE%97%E6%B3%95

程序实现

假定有如下的地图：

黑色边框为障碍物，要求找到左下角x到右上角x的最短距离，而且每次只能向周围（上、下、左、右、左上、左下、右上、右下）八个点移动

接下来使用Dijkstra算法来解决这个问题，先看最终效果：

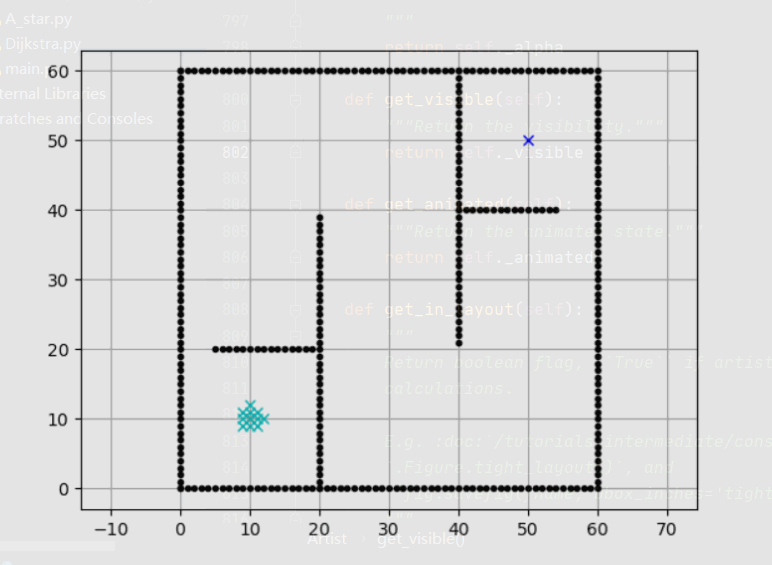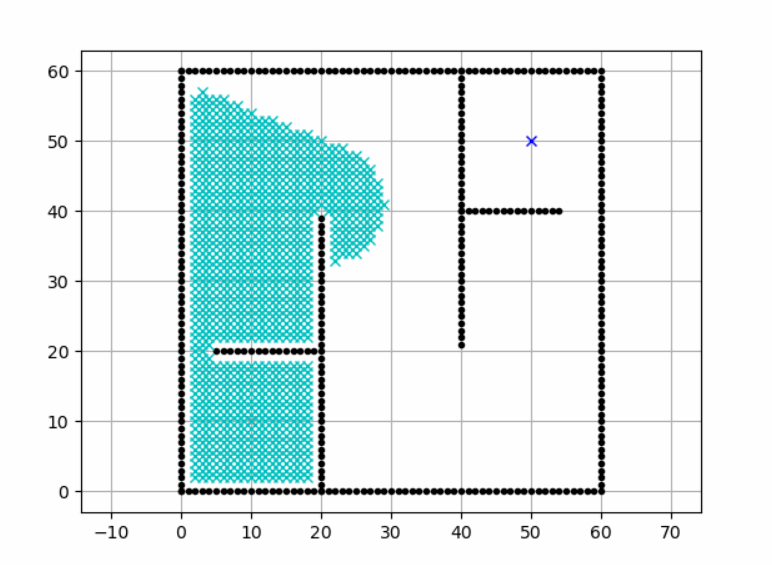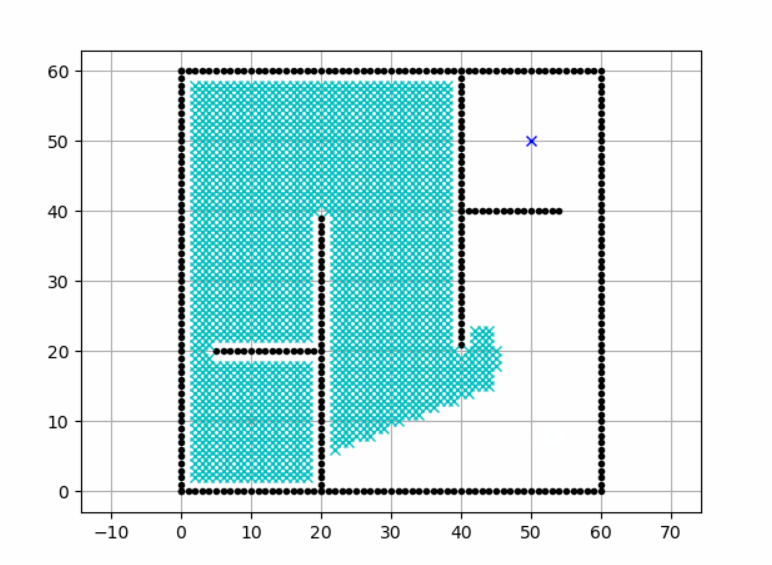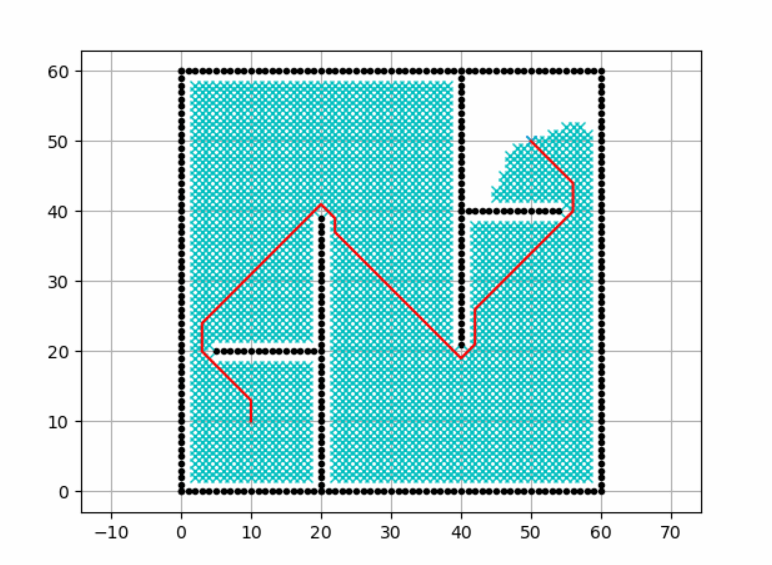
节点类

为了解决这个问题，我们还需要定义一个节点类，包括自身位置、与开始位置的最短距离，以及在最短路径中前一个节点的索引

class Node:
    def __init__(self, x, y, cost, pind):
        self.x = x # 自身位置的x坐标
        self.y = y # 自身位置的y坐标
        self.cost = cost # 与开始位置的最短距离
        self.pind = pind # 在最短路径中位于当前节点的前一个节点的索引

    def __str__(self):
        return str(self.x) + "," + str(self.y) + "," + str(self.cost) + "," + str(self.pind)

初始化开始位置、目标位置、地图

sx = 10.0 # 开始位置的x坐标
sy = 10.0 # 开始位置的y坐标
gx = 50.0 # 目标位置的x坐标
gy = 50.0 # 目标位置的y坐标
grid_size = 1.0 # 网格大小
robot_size = 1.0 # 机器人大小

ox = [] # 障碍物的x坐标列表
oy = [] # 障碍物的y坐标列表

# 向地图中添加障碍物
for i in range(60):
    ox.append(i)
    oy.append(0.0)
for i in range(60):
    ox.append(60.0)
    oy.append(i)
for i in range(61):
    ox.append(i)
    oy.append(60.0)
for i in range(61):
    ox.append(0.0)
    oy.append(i)
for i in range(40):
    ox.append(20.0)
    oy.append(i)
for i in range(40):
    ox.append(40.0)
    oy.append(60.0 - i)
for i in range(15):
    ox.append(5.0 + i)
    oy.append(20)
for i in range(15):
    ox.append(40.0 + i)
    oy.append(40)

# 画出障碍物、开始位置、目标位置
plt.plot(ox, oy, ".k")
plt.plot(sx, sy, "xr")
plt.plot(gx, gy, "xb")
plt.grid(True)
plt.axis("equal")

nstart = Node(round(sx / grid_size), round(sy / grid_size), 0.0, -1)
ngoal = Node(round(gx / grid_size), round(gy / grid_size), 0.0, -1)
ox = [iox / grid_size for iox in ox]
oy = [ioy / grid_size for ioy in oy]

# 生成障碍物地图
obmap, minx, miny, maxx, maxy, xw, yw = calc_obstacle_map(ox, oy, grid_size, robot_size)
# 节点的可能移动情况
# x方向位移，y方向位移，移动距离
motion = [[ 1,  0, 1],
          [ 0,  1, 1],
          [-1,  0, 1],
          [ 0, -1, 1],
          [-1, -1, math.sqrt(2)],
          [-1,  1, math.sqrt(2)],
          [ 1, -1, math.sqrt(2)],
          [ 1,  1, math.sqrt(2)]]

Dijkstra算法的处理过程

初始化完成后，就是算法的循环过程：每次扩展一个距离最短的点，并更新与其相邻的点的距离

# 已扩展的节点，未扩展的节点
openset, closedset = dict(), dict()
# 将开始位置加入已扩展节点字典
openset[calc_index(nstart, xw, minx, miny)] = nstart

while True:
    # 找到未扩展节点中距离最小的节点
    c_id = min(openset, key=lambda o: openset[o].cost)
    current = openset[c_id]
    print("current", current)

    # 显示当前扩展的节点
    plt.plot(current.x * grid_size, current.y * grid_size, "xc")
    if len(closedset.keys()) % 10 == 0: # 显示10个节点后暂停一下
        plt.pause(0.001)
        # pass

    # 判断当前扩展的节点是不是目标节点
    if current.x == ngoal.x and current.y == ngoal.y:
        print("Find goal")
        ngoal.pind = current.pind
        ngoal.cost = current.cost
        break # 如果是则退出循环

    # 将当前扩展的节点从未扩展节点字典中剔除
    del openset[c_id]
    # 将当前扩展的节点添加到已扩展节点字典
    closedset[c_id] = current

    # 循环将当前扩展节点周围的节点加入到未扩展节点字典
    for i, _ in enumerate(motion):
        node = Node(current.x + motion[i][0], current.y + motion[i][1],
                    current.cost + motion[i][2], c_id)
        n_id = calc_index(node, xw, minx, miny)

        # 判断该节点是否在地图外或者处于障碍物上
        if not verify_node(node, obmap, minx, miny, maxx, maxy):
            # 是则进入下一轮循环
            continue

        # 如果该节点已经被扩展了，则进入下一轮循环
        if n_id in closedset:
            continue
        # 如果该节点已经在未扩展节点字典中，则更新它到开始位置的最短距离
        if n_id in openset:
            if openset[n_id].cost > node.cost:
                openset[n_id].cost = node.cost
                openset[n_id].pind = c_id
        # 否则加入到未扩展节点字典中
        else:
            openset[n_id] = node

计算最终路径

# 计算最终路径
rx, ry = [ngoal.x * grid_size], [ngoal.y * grid_size]
pind = ngoal.pind
# 从最终节点依次向前递推得到最短路径
while pind != -1:
    n = closedset[pind]
    rx.append(n.x * grid_size)
    ry.append(n.y * grid_size)
    pind = n.pind
plt.plot(rx, ry, "-r")
plt.show()

程序中用到的一些函数

# 判断节点是否在地图外或者处于障碍物上
def verify_node(node, obmap, minx, miny, maxx, maxy):
    if obmap[node.x][node.y]:
        return False
    if node.x < minx:
        return False
    elif node.y < miny:
        return False
    elif node.x > maxx:
        return False
    elif node.y > maxy:
        return False
    return True

def calc_obstacle_map(ox, oy, grid_size, vr):
    # 四舍五入取整
    minx = round(min(ox))
    miny = round(min(oy))
    maxx = round(max(ox))
    maxy = round(max(oy))
    xwidth = round(maxx - minx)
    ywidth = round(maxy - miny)

    # 障碍物地图生成
    # 有障碍物为True，否则为False
    obmap = [[False for i in range(ywidth)] for i in range(xwidth)]
    for ix in range(xwidth):
        x = ix + minx
        for iy in range(ywidth):
            y = iy + miny
            for iox, ioy in zip(ox, oy): # zip：将对象打包为一个个元组
                d = math.sqrt((iox - x)**2 + (ioy - y)**2)
                if d <= vr / grid_size:
                    obmap[ix][iy] = True
                    break
    return obmap, minx, miny, maxx, maxy, xwidth, ywidth

def calc_index(node, xwidth, xmin, ymin):
    # 返回节点在地图中的索引：y*xw+x
    return (node.y - ymin) * xwidth + (node.x - xmin)

程序参考：https://github.com/AtsushiSakai/PythonRobotics