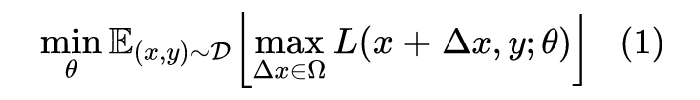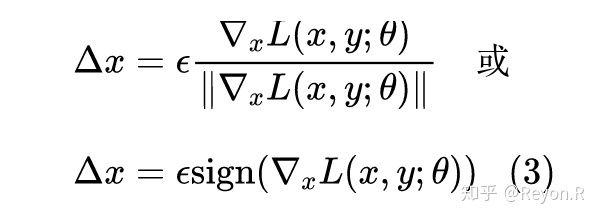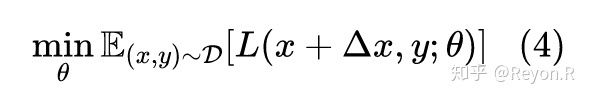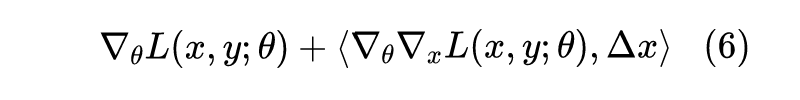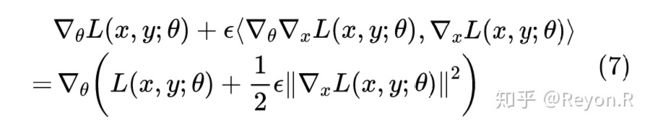图像embedding训练方式_转载 | 对抗训练浅谈：意义、方法和思考（附Keras实现）...

本文转载自公众号：PaperWeekly (paperweekly)

整理编辑 | PaperWeekly

©PaperWeekly 原创 · 作者｜苏剑林

单位｜追一科技

研究方向｜NLP、神经网络

当前，说到深度学习中的对抗，一般会有两个含义：一个是生成对抗网络（Generative Adversarial Networks，GAN），代表着一大类先进的生成模型；另一个则是跟对抗攻击、对抗样本相关的领域，它跟 GAN 相关，但又很不一样，它主要关心的是模型在小扰动下的稳健性。

本人之前所涉及的对抗话题，都是前一种含义，而今天，我们来聊聊后一种含义中的“对抗训练”。

本文包括如下内容：

1. 对抗样本、对抗训练等基本概念的介绍；
2. 介绍基于快速梯度上升的对抗训练及其在 NLP 中的应用；
3. 给出了对抗训练的 Keras 实现（一行代码调用）；
4. 讨论了对抗训练与梯度惩罚的等价性；
5. 基于梯度惩罚，给出了一种对抗训练的直观的几何理解。

方法介绍

近年来，随着深度学习的日益发展和落地，对抗样本也得到了越来越多的关注。

在 CV 领域，我们需要通过对模型的对抗攻击和防御来增强模型的稳健型，比如在自动驾驶系统中，要防止模型因为一些随机噪声就将红灯识别为绿灯。

在 NLP 领域，类似的对抗训练也是存在的，不过 NLP 中的对抗训练更多是作为一种正则化手段来提高模型的泛化能力。

这使得对抗训练成为了 NLP 刷榜的“神器”之一，前有微软通过 RoBERTa+ 对抗训练在 GLUE [1] 上超过了原生 RoBERTa，后有我司的同事通过对抗训练刷新了 CoQA [2] 榜单。这也成功引起了笔者对它的兴趣，遂学习了一番，分享在此。

基本概念

要认识对抗训练，首先要了解“对抗样本”，它首先出现在论文Intriguing properties of neural networks[3]之中。

简单来说，它是指对于人类来说“看起来”几乎一样、但对于模型来说预测结果却完全不一样的样本，比如下面的经典例子：

理解对抗样本之后，也就不难理解各种相关概念了，比如“对抗攻击”，其实就是想办法造出更多的对抗样本，而“对抗防御”，就是想办法让模型能正确识别更多的对抗样本。

所谓对抗训练，则是属于对抗防御的一种，它构造了一些对抗样本加入到原数据集中，希望增强模型对对抗样本的鲁棒性；同时，如本文开篇所提到的，在 NLP 中它通常还能提高模型的表现。

Min-Max

总的来说，对抗训练可以统一写成如下格式：

其中 代表训练集，代表输入，代表标签，是模型参数，是单个样本的 loss，是对抗扰动，是扰动空间。这个统一的格式首先由论文Towards Deep Learning Models Resistant to Adversarial Attacks[4] 提出。这个式子可以分步理解如下：

1. 往属于里边注入扰动 ，的目标是让 越大越好，也就是说尽可能让现有模型的预测出错；
2. 当然 也不是无约束的，它不能太大，否则达不到“看起来几乎一样”的效果，所以 要满足一定的约束，常规的约束是 ，其中 是一个常数；
3. 每个样本都构造出对抗样本之后，用作为数据对去最小化loss来更新参数 （梯度下降）；
4. 反复交替执行 1、2、3 步。

由此观之，整个优化过程是 和 交替执行，这确实跟 GAN 很相似，不同的是，GAN 所 的自变量也是模型的参数，而这里 的自变量则是输入（的扰动量），也就是说要对每一个输入都定制一步 。

快速梯度

现在的问题是如何计算 ，它的目标是增大 ，而我们知道让 loss 减少的方法是梯度下降，那反过来，让 loss 增大的方法自然就是梯度上升，因此可以简单地取：

当然，为了防止 过大，通常要对 做些标准化，比较常见的方式是：

有了 之后，就可以代回式 (1) 进行优化：

这就构成了一种对抗训练方法，被称为 Fast Gradient Method（FGM），它由 GAN 之父 Goodfellow 在论文 Explaining and Harnessing Adversarial Examples [5] 首先提出。

此外，对抗训练还有一种方法，叫做 Projected Gradient Descent（PGD），其实就是通过多迭代几步来达到让 更大的 。如果迭代过程中模长超过了 ，就缩放回去，细节请参考Towards Deep Learning Models Resistant to Adversarial Attacks[6]。但本文不旨在对对抗学习做完整介绍，而且笔者认为它不如 FGM 漂亮有效，所以本文还是以 FGM 为重点。关于对抗训练的补充介绍，建议有兴趣的读者阅读富邦同学写的功守道：NLP中的对抗训练 + PyTorch实现。

回到NLP

对于 CV 领域的任务，上述对抗训练的流程可以顺利执行下来，因为图像可以视为普通的连续实数向量，也是一个实数向量，因此 依然可以是有意义的图像。但 NLP 不一样，NLP 的输入是文本，它本质上是 one hot 向量（如果还没认识到这一点，欢迎阅读词向量与 Embedding 究竟是怎么回事？[7]，而两个不同的 one hot 向量，其欧氏距离恒为 ，因此对于理论上不存在什么“小扰动”。

一个自然的想法是像论文 Adversarial Training Methods for Semi-Supervised Text Classification [8] 一样，将扰动加到 Embedding 层。

这个思路在操作上没有问题，但问题是，扰动后的 Embedding 向量不一定能匹配上原来的 Embedding 向量表，这样一来对 Embedding 层的扰动就无法对应上真实的文本输入，这就不是真正意义上的对抗样本了，因为对抗样本依然能对应一个合理的原始输入。

那么，在 Embedding 层做对抗扰动还有没有意义呢？有！实验结果显示，在很多任务中，在 Embedding 层进行对抗扰动能有效提高模型的性能。

实验结果

既然有效，那我们肯定就要亲自做实验验证一下了。怎么通过代码实现对抗训练呢？怎么才能做到用起来尽可能简单呢？最后用起来的效果如何呢？

思路分析

对于 CV 任务来说，一般输入张量的 shape 是 ，这时候我们需要固定模型的 batch size（即），然后给原始输入加上一个 shape 同样为 、全零初始化的Variable。比如就叫做 ，那么我们可以直接求 loss 对 的梯度，然后根据梯度给 赋值，来实现对输入的干扰，完成干扰之后再执行常规的梯度下降。对于 NLP 任务来说，原则上也要对 Embedding 层的输出进行同样的操作，Embedding 层的输出 shape 为 ，所以也要在 Embedding 层的输出加上一个 shape 为 的Variable，然后进行上述步骤。但这样一来，我们需要拆解、重构模型，对使用者不够友好。

不过，我们可以退而求其次。Embedding 层的输出是直接取自于 Embedding 参数矩阵的，因此我们可以直接对 Embedding 参数矩阵进行扰动。

这样得到的对抗样本的多样性会少一些（因为不同样本的同一个 token 共用了相同的扰动），但仍然能起到正则化的作用，而且这样实现起来容易得多。

代码参考

基于上述思路，这里给出 Keras 下基于 FGM 方式对 Embedding 层进行对抗训练的参考实现：

https://github.com/bojone/keras_adversarial_training

核心代码如下：

def adversarial_training(model, embedding_name, epsilon=1):
    """给模型添加对抗训练
    其中model是需要添加对抗训练的keras模型，embedding_name
    则是model里边Embedding层的名字。要在模型compile之后使用。
    """
    if model.train_function is None:  # 如果还没有训练函数
        model._make_train_function()  # 手动make
    old_train_function = model.train_function  # 备份旧的训练函数

    # 查找Embedding层
    for output in model.outputs:
        embedding_layer = search_layer(output, embedding_name)
        if embedding_layer is not None:
            break
    if embedding_layer is None:
        raise Exception('Embedding layer not found')

    # 求Embedding梯度
    embeddings = embedding_layer.embeddings  # Embedding矩阵
    gradients = K.gradients(model.total_loss, [embeddings])  # Embedding梯度
    gradients = K.zeros_like(embeddings) + gradients[0]  # 转为dense tensor

    # 封装为函数
    inputs = (model._feed_inputs +
              model._feed_targets +
              model._feed_sample_weights)  # 所有输入层
    embedding_gradients = K.function(
        inputs=inputs,
        outputs=[gradients],
        name='embedding_gradients',
    )  # 封装为函数

    def train_function(inputs):  # 重新定义训练函数
        grads = embedding_gradients(inputs)[0]  # Embedding梯度
        delta = epsilon * grads / (np.sqrt((grads**2).sum()) + 1e-8)  # 计算扰动
        K.set_value(embeddings, K.eval(embeddings) + delta)  # 注入扰动
        outputs = old_train_function(inputs)  # 梯度下降
        K.set_value(embeddings, K.eval(embeddings) - delta)  # 删除扰动
        return outputs

    model.train_function = train_function  # 覆盖原训练函数

定义好上述函数后，给 Keras 模型增加对抗训练就只需要一行代码了：

# 写好函数后，启用对抗训练只需要一行代码
adversarial_training(model, 'Embedding-Token', 0.5)

需要指出的是，由于每一步算对抗扰动也需要计算梯度，因此每一步训练一共算了两次梯度，因此每步的训练时间会翻倍。

效果比较

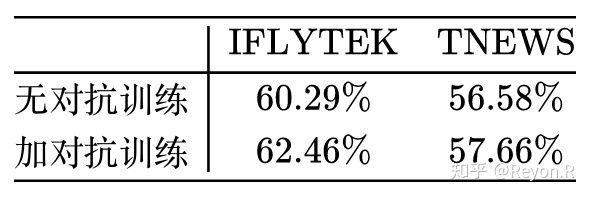
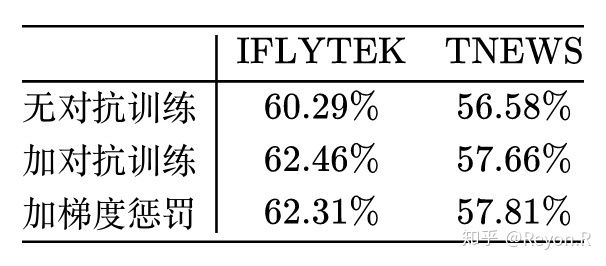
为了测试实际效果，笔者选了中文 CLUE 榜 [9] 的两个分类任务：IFLYTEK和TNEWS，模型选择了中文 BERT base。

在 CLUE 榜单上，BERT base 模型在这两个数据上的成绩分别是 60.29% 和56.58%，经过对抗训练后，成绩为 62.46%、57.66%，分别提升了 2% 和 1%！

训练脚本请参考：https://github.com/bojone/bert4keras/blob/master/examples/task_iflytek_adversarial_training.py

当然，同所有正则化手段一样，对抗训练也不能保证每一个任务都能有提升，但从目前大多数“战果”来看，它是一种非常值得尝试的技术手段。

此外，BERT 的 finetune 本身就是一个非常玄乎（靠人品）的过程，前些时间论文Fine-Tuning Pretrained Language Models: Weight Initializations, Data Orders, and Early Stopping[10]换用不同的随机种子跑了数百次 finetune 实验，发现最好的结果能高出好几个点，所以如果你跑了一次发现没提升，不妨多跑几次再下结论。

延伸思考

在这一节中，我们从另一个视角对上述结果进行分析，从而推出对抗训练的另一种方法，并且得到一种关于对抗训练的更直观的几何理解。

梯度惩罚

假设已经得到对抗扰动 ，那么我们在更新 时，考虑对 的展开：

对应的 的梯度为：

代入 ，得到：

这个结果表示，对输入样本施加 的对抗扰动，一定程度上等价于往 loss 里边加入梯度惩罚。

如果对抗扰动是 ，那么对应的梯度惩罚项则是 （少了个，也少了个2次方）。

事实上，这个结果不是新的，据笔者所知，它首先出现论文 Improving the Adversarial Robustness and Interpretability of Deep Neural Networks by Regularizing their Input Gradients [11] 里。

只不过这篇文章不容易搜到，因为你一旦搜索“adversarial training gradient penalty”等关键词，出来的结果几乎都是 WGAN-GP 相关的东西。

几何图像

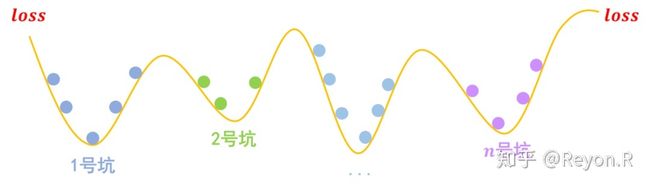
事实上，关于梯度惩罚，我们有一个非常直观的几何图像。以常规的分类问题为例，假设有 个类别，那么模型相当于挖了 个坑，然后让同类的样本放到同一个坑里边去：

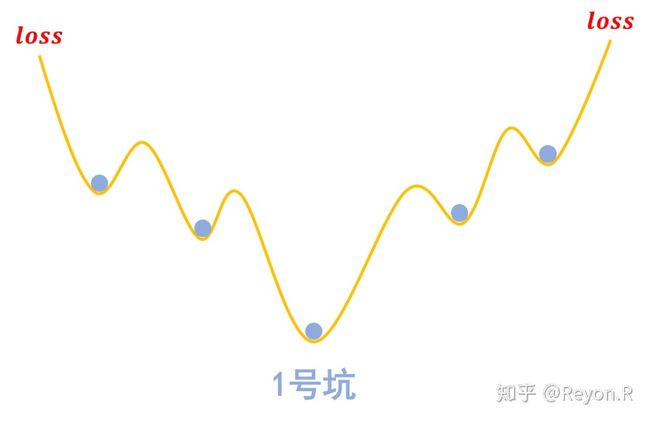
梯度惩罚则说同类样本不仅要放在同一个坑内，还要放在坑底，这就要求每个坑的内部要长这样：

为什么要在坑底呢？因为物理学告诉我们，坑底最稳定呀，所以就越不容易受干扰呀，这不就是对抗训练的目的么？

那坑底意味着什么呢？极小值点呀，导数（梯度）为零呀，所以不就是希望 越小越好么？这便是梯度惩罚 (8) 的几何意义了。类似的“挖坑”、“坑底”与梯度惩罚的几何图像，还可以参考能量视角下的GAN模型：GAN＝“挖坑”＋“跳坑”。

L约束

我们还可以从 L 约束（Lipschitz 约束）的角度来看梯度惩罚。所谓对抗样本，就是输入的小扰动导致输出的大变化，而关于输入输出的控制问题，我们之前在文章深度学习中的Lipschitz约束：泛化与生成模型就已经探讨过。

一个好的模型，理论上应该是“输入的小扰动导致导致输出的小变化”，而为了保证这一遍，一个很常用的方案是让模型满足 L 约束，即存在常数 ，使得

这样一来只要两个输出的差距 足够小，那么就能保证输出的差距也足够小。

而深度学习中的Lipschitz约束：泛化与生成模型已经讨论了，实现 L 约束的方案之一就是谱归一化（Spectral Normalization），所以往神经网络里边加入谱归一化，就可以增强模型的对抗防御性能。

相关的工作已经被发表在 Generalizable Adversarial Training via Spectral Normalization [12]。

美中不足的是，谱归一化是对模型的每一层权重都进行这样的操作，结果就是神经网络的每一层都满足 L 约束，这是不必要的（我们只希望整个模型满足 L 约束，不必强求每一层都满足），因此理论上来说 L 约束会降低模型表达能力，从而降低模型性能。

而在 WGAN 系列模型中，为了让判别器满足 L 约束，除了谱归一化外，还有一种常见的方案，那就是梯度惩罚。因此，梯度惩罚也可以理解为一个促使模型满足 L 约束的正则项，而满足 L 约束则能有效地抵御对抗样本的攻击。

代码实现

既然梯度惩罚号称能有类似的效果，那必然也是要接受实验验证的了。相比前面的 FGM 式对抗训练，其实梯度惩罚实现起来还容易一些，因为它就是在 loss 里边多加一项罢了，而且实现方式是通用的，不用区分 CV 还是 NLP。

Keras 参考实现如下：

def sparse_categorical_crossentropy(y_true, y_pred):
    """自定义稀疏交叉熵
    这主要是因为keras自带的sparse_categorical_crossentropy不支持求二阶梯度。
    """
    y_true = K.reshape(y_true, K.shape(y_pred)[:-1])
    y_true = K.cast(y_true, 'int32')
    y_true = K.one_hot(y_true, K.shape(y_pred)[-1])
    return K.categorical_crossentropy(y_true, y_pred)


def loss_with_gradient_penalty(y_true, y_pred, epsilon=1):
    """带梯度惩罚的loss
    """
    loss = K.mean(sparse_categorical_crossentropy(y_true, y_pred))
    embeddings = search_layer(y_pred, 'Embedding-Token').embeddings
    gp = K.sum(K.gradients(loss, [embeddings])[0].values**2)
    return loss + 0.5 * epsilon * gp


model.compile(
    loss=loss_with_gradient_penalty,
    optimizer=Adam(2e-5),
    metrics=['sparse_categorical_accuracy'],
)

可以看到，定义带梯度惩罚的 loss 非常简单，就两行代码而已。需要指出的是，梯度惩罚意味着参数更新的时候需要算二阶导数，但是 Tensorflow 和 Keras 自带的 loss 函数不一定支持算二阶导数。

比如K.categorical_crossentropy支持而K.sparse_categorical_crossentropy不支持，遇到这种情况时，需要自定重新定义 loss。

效果比较

还是前面两个任务，结果如下表。可以看到，梯度惩罚能取得跟 FGM 基本一致的结果。

完整的代码请参考：

https://github.com/bojone/bert4keras/blob/master/examples/task_iflytek_gradient_penalty.py

本文小结

本文简单介绍了对抗训练的基本概念和推导，着重讲了其中的 FGM 方法并给出了 Keras 实现，实验证明它能提高一些 NLP 模型的泛化性能。此外，本文还讨论了对抗学习与梯度惩罚的联系，并给出了梯度惩罚的一种直观的几何理解。

相关链接

[1] https://gluebenchmark.com/leaderboard[2] https://stanfordnlp.github.io/coqa/[3] http://https://arxiv.org/abs/1312.6199[4] https://arxiv.org/abs/1706.06083[5] https://arxiv.org/abs/1412.6572[6] https://arxiv.org/abs/1706.06083[7] https://kexue.fm/archives/4122[8] https://arxiv.org/abs/1605.07725[9] https://www.cluebenchmarks.com/[10] https://arxiv.org/abs/2002.06305[11] https://arxiv.org/abs/1711.09404[12] https://arxiv.org/abs/1811.07457

​