转发自http://crickcollege.com/news/237.html
前言
在以往的推文中,小编给大家整理了两篇有关假设检验的推文,其说明的主要问题是:1. 什么是假设检验?2. 假设检验的方法有哪些?
往期推文
聊聊绕不开的假设检验
【新春大礼】假设检验方法大集合
在进行假设检验分析数据时,其实是有这么一个简单的逻辑:
也就是说,在我们对数据(尤其是数据量较大的时候)进行假设检验以后(也就是我们常称的“多重检验”),得到了对应的P值,这时候不要高兴太早,你还没有分析完,接下来,你其实还要对得到的P值进行校正,然后使用校正后的P值进行后续的分析。
那么,问题就来了:我们为什么要对多重检验得到的P值进行校正呢?其实关键点还是在这个“多”字上!中国老话都说了,“常在河边走哪有不湿鞋”,“言多必失”,这绝对是有统计学思想在里面的,只是我们先人没有将其归纳总结成数学理论罢了。
这里推荐小伙伴们详细读一读以下这篇推文, 尤其是对统计学基础理论需要先了解一下的小伙伴们,后面提到的校正方法中有两种的原理介绍都在这篇推文里有详细的描述,小编就不再赘述了。
人气推文p值、E值、FDR、q值…你晕菜了吗?续集来啦!
那么如何对P值进行校正呢?接下来,小编要给大家详细地介绍4种常用的P值校正方法,每一种方法都有其一定的适用性。小编还附上了这些方法的R语言实现,很贴心吧?在这里我们要感谢开发这些方法的牛人们!
Notes
进行P值校正的方法绝对不止小编介绍的这几种,挑选出来的这些,一是很常用,二是小编自己比较熟悉。感兴趣的同学还可以去学习更多的方法。
下面小编就一一给大家介绍这些方法,如果有叙述有不妥之处,还请大伙儿慷慨指证,互相学习。
来个总表先
现在,小编就开始把上面列表的方法一一做下使用介绍,包括所使用的R函数,该函数的介绍,以及举个实例进行解释说明。
Tips
小编在前面的推文里也提到过,在R语言里,使用“?”或者“help”命令可以对每一个函数进行查询,看其详细的介绍。
p.adjust校正
(参考文献:http://www.jstor.org/stable/2346101,DOI: 10.2307/2532694)
R函数:
其中p是指多重检验得到的P值,method是选择一种校正的方法(下文有具体介绍),n就是输入p值的个数。
函数介绍:
该函数是嵌入到基础包stats中,所以不需要额外安装,可直接进行使用。目前,该函数所具有的校正方法主要有以下几种:
其中“bonferroni”和“BH”法是我们常见的方法,其介绍也可以参考上面提到的那期推文。在这里小编只强调一点,“bonferroni”方法进行校正是最严格的,所以这种方法一般大家都不采用。
举例说明:
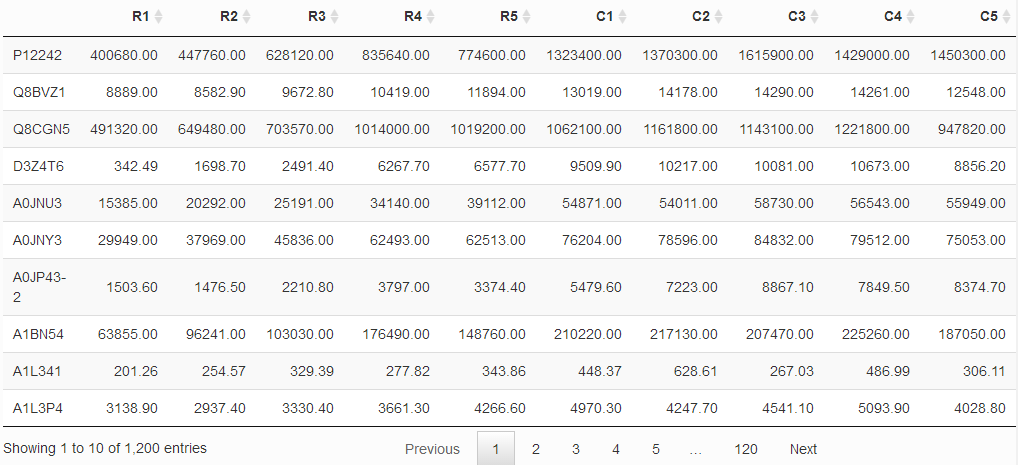
以蛋白质定量数据为例(PS:没有特别说明,小编都以此数据为示例数据)。我们假设现在有两大组数据(R, C),每一组得到5次生物学重复的数据,其中总共鉴定到1200个蛋白质。得到数据如下:
然后使用某一种或者两种假设检验的方法得到每一个蛋白质对应的P值,读到R中。我们使用head函数进行查看读进来的前20个数据,如下:
然后使用p.adjust函数,选用“BH”方法,如下:
如感兴趣,也可以选择其他的方法进行尝试。
fdrci法
(参考文献:doi:10.3389/fgene.2013.00179)
R函数:
在这个方法中主要有三种函数,分别实现不同的功能:
其中obsp是指多重检验得到的P值,permp是指置换抽样得到的P值数据框列表,pnm是指P值数据框中对应P值的列名,ntests是指进行多重检验的个数,thres是指显著性阈值,cl是指置信水平。
其中obs_vec是指多重检验得到的P值,perm_list是指置换抽样得到的P值数据框列表,pname是指P值数据框中对应P值的列名,ntests是指进行多重检验的个数,lowerbound是指-log10(P)的下限,upperbound是指-log10(P)的上限,incr是指每次递增的步数,cl是指置信水平。
plotdat是指fdrTbl函数得到的结果,lowerbound是指-log10(P)的下限,upperbound是指-log10(P)的上限,mn是指画图的主题名字,lpos是指图例的位置,outfile是指是否保存图形,若为FASLE表示直接画图,若为一名字表示将画出的图形保存成该名字的图片。
函数介绍:
置换抽样法估计FDR的核心思想就是:利用置换抽样的思想,得出一系列的置换结果,然后将该结果与原始的观测值进行比较,从而估算出对应的FDR。
上述的3个函数各自的功能是,fdr_od是根据设置的阈值进行一次的FDR估计;fdrTbl是根据设置的上下界限(-log10(P)的值),按照增加的步长,逐步的计算对应阈值下的FDR;FDRplot是将fdrTbl的结果可视化。
置换抽样检验,举个简单的小例子进行说明其操作过程,比如我们现在利用置换检验的方法来检验某一蛋白质在两组中的差异,怎么做呢?
1
a:读入该蛋白质在两组各重复中的定量值
b : 计算二者的均值差,这就是我们原始的观测值
c : 将X,Y两组数据放在一组之中,组成一个集合
d : 对XYgroup中的数据随机抽取5个组合成X’,剩下的为Y’,然后计算X’与Y’之间的均值
e : 重复d步骤1000次,这样就可以得到1000个置换抽样的结果,然后统计其中大于objXY的个数,比如说有10个,那么此时置换抽样检验得到相应的P值就等于10/1000=0.01
举例说明:
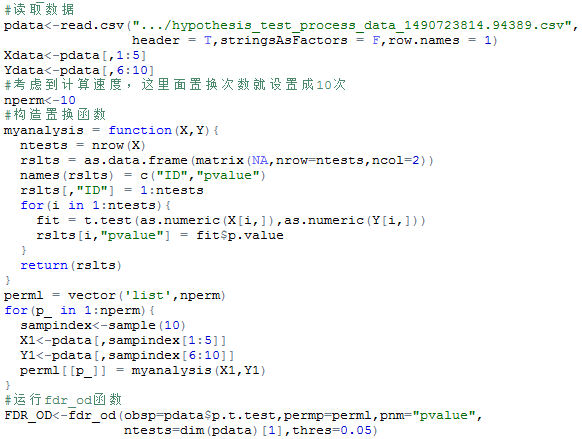
还是使用上述的数据,进行置换抽样法计算FDR,代码如下:
运行的结果为:
该结果中,从左到右的含义依次为:
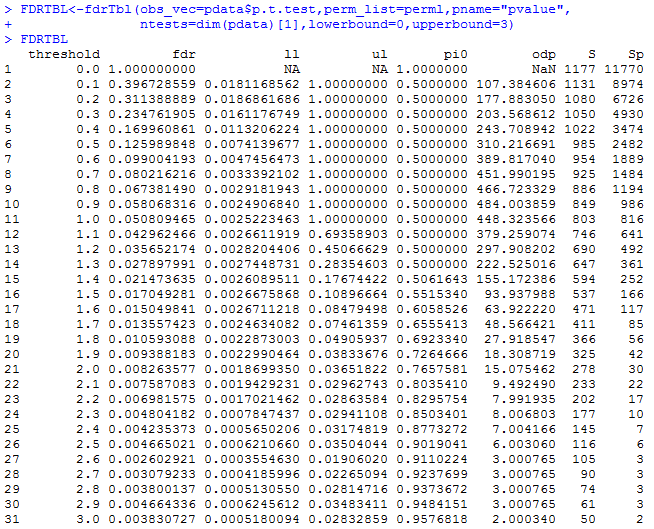
翻译一下就是,FDR,即是在设置0.05的阈值下(thres参数)估计出来的FDR值;ll和ul分别为FDR置信区间的下限和上下;pi0是指真实原假设的比例;c1是估计出的扩散参数;ro是指原始观察值中正检测的个数(即原始P值小于等于设定阈值0.05的个数);vp1是指所有置信抽样结果中正检测的个数。
运行fdrTbl函数:
正如上面所描述的那样,fdrTbl函数就是在每一个阈值下进行FDR估计,并将所有结果汇总在一个表格中。
运行FDRplot函数:
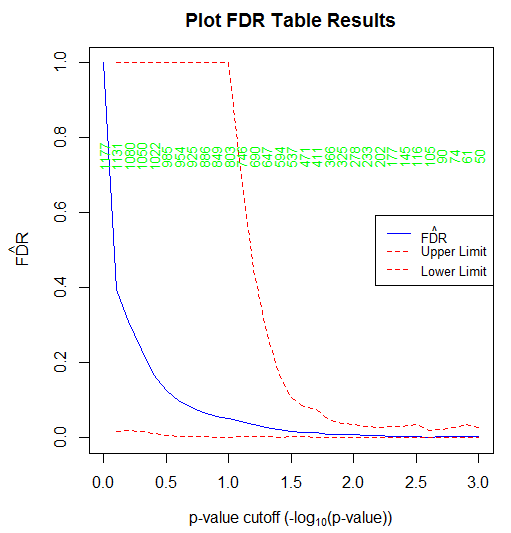
可得如下图形:
可以看出,该函数就是将fdrTbl的结果进行可视化。对该图形的解读就是:蓝色的实线就是在每一个阈值下估计出来的FDR值,上述的函数中,我们设置的0是下限,3是上限,所以也可以发现该图形的x轴的范围是[0, 3];红色的虚线是估计对应的上下置信区间;我们还可以发现图形中间还有一串绿色的数字,它们的含义是指原始观察值中正检测的个数(即原始P值小于等于对应阈值的个数),也就是上述fdrTbl函数计算结果中S的那一列数据。
qvalue法
R函数:
其中p是指多重检验得到的P值;fdr.level就是设定fdr的阈值,设定这个值后,会在结果中展示出校正后的P值与这个阈值比较的结果,小于就是TRUE,大于就是FALSE;pfdr是指是否对较小的P值进行更加稳健的估计。
函数介绍:
该方法最开始由Storey提出,俗称“正假发现率”,即positive false discovery rate。详细说明可以参考上述推荐的推文,其中较为详细的介绍了qvalue的原理,并且也解释了什么是全局FDR(global FDR),什么是局部FDR(local FDR)。对于这两种FDR,小编在这里多啰嗦几句,介绍如下,
简单些来讲,全局FDR是计算一堆对象(比如鉴定到的所有蛋白质)的FDR,局部FDR是计算一个对象(比如某一个蛋白质)的FDR。为什么会有这种情况呢?是因为,全局FDR只能告诉我们一个整体的情况,而局部FDR却能告诉我们某一个对象的假发现率,这更像是一个可信度(越小越可信),所以当你很想确定某一个蛋白质的假阳性率的时候,这时候你就可以考虑计算一下它的局部FDR。
在计算的层面上,可以理解为,局部FDR是全局FDR的导数,数学公式推导,这里就不展示了,感兴趣的可查阅相关文献(doi: 10.1021/pr070492f.)。
举例说明:
我们仍然使用上述数据,使用函数如下:
使用qvalue函数以后,结果中包含多个list,其中校正后的P值(可理解为全局FDR)存在qvalues这个对象中,估计的局部FDR存在lfdr这个对象中。我们可以像这样把对应的对象提出来,并查看:
此外,该方法的开发者还写了一个用户界面,不需要每次都敲写代码,方便大家使用。不过需要指出一点的是,在新版本的qvalue包中,这个功能已经被取消了,所以想使用这个功能的话,需要下载比较低的版本,以及在比较低版本的R中运行才行。运行如下进行调用该界面:
运行后打开如下界面:
使用起来也很简便,一般来讲,默认的参数就已经可以满足大多数计算需求,所以只需要点击“Browse”导入数据,然后点击“Execute”执行就行,计算出来的结果也可以进行直接保存。
fdrtool工具包
(参考文献:
doi:10.1093/bioinformatics/btn209)
R函数:
其中x是指多重检验得到的P值、z统计量或者t统计量,亦或是相关性系数;statistic与前面x的类型对应,其中z统计量或者t统计量对应“normal”,相关性系数对应“correlation”,多重检验得到的P值对应“pvalue”;plot指是否画图;color.figure指画图中是否用颜色区分;verbose指是否显示计算的过程描述;cutoff.method是指选择一种取分界点的方法;pct0这个参数,只有当cutoff.method取“pct0”时才管用。
函数介绍:
该函数计算的基本思想就是使用经验贝叶斯方法,假设研究的对象分为两部分(null, non-null),可理解为显著和不显著两部分,从二者的混合分布中计算出null部分所占的比例。此外,开发该包的作者集成了多种方法,可分析的对象种类比较多,使其使用起来也比较方便。
举例说明:
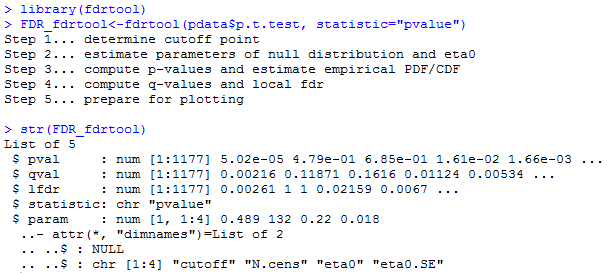
依然是使用上述的示例数据,其函数使用如下,
由于我们输入的是多重检验得到的P值,所以对应的statistic选择了“pvalue”。从结果中可以发现,该方法可以得出全局FDR值,保存在qval对象中,也可以得到局部FDR值,保存在lfdr对象中,分别可以运行如下代码进行提取和查看其中的数值:
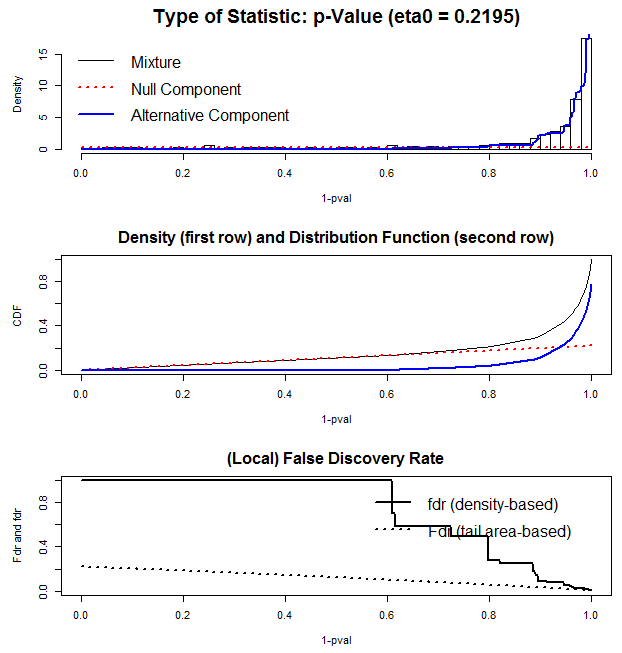
与此同时,该函数还画出了对应的结果图形,如下:
从上到下来看这个结果,图形的题目告诉我们选用的是哪类分析对象,并给出null部分占比的估计值(eta0);第一行的图是展现概率密度的柱状分布图以及两份拟合的概率分布图;第二行展现了对应的累计概率密度分布函数;第三行展现了估计的全局FDR和局部FDR的分布。
小结一下
在本文中,小编主要给大家较为详细的介绍了4种P值校正的方法(p.adjust, fdrci, qvalue, fdrtool),小编在这里不对这些方法进行比较,也不下结论说哪种方法好,哪种方法不好。数据分析还是以大家的分析目的为主要指导思想,方法只是一种工具,选择能解释你数据的才是最好的。最后,小编也希望大家有时间可以自己动手重现上述的代码(尤其是你以前没有用过的方法),自己体验一下,也许会给你的分析带来一点新的思路。