力扣160. 相交链表 哈希、双指针、差值法、栈四种花式解法
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
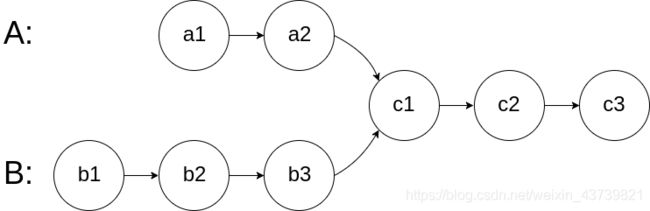
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
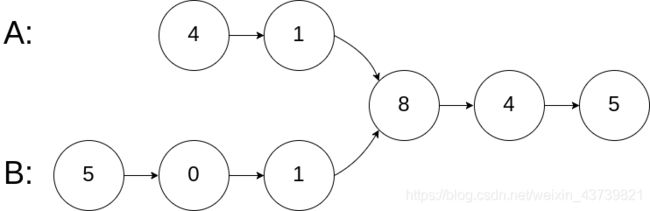
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
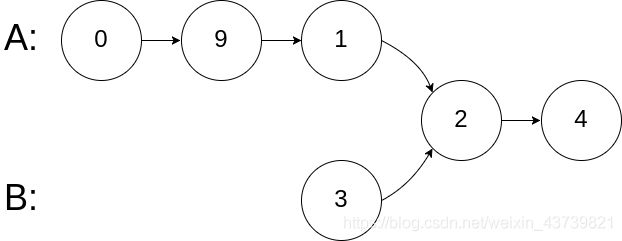
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
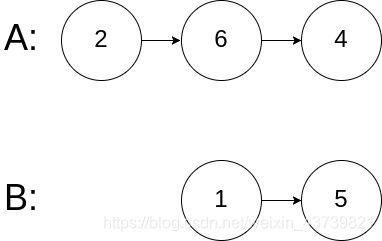
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 m
listB 中节点数目为 n
0 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点,intersectVal 为 0
如果 listA 和 listB 有交点,intersectVal == listA[skipA + 1] == listB[skipB + 1]
进阶:你能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案?
解法一:哈希表法
遍历第一个链表,将其结点全部存入哈希表,再遍历第二个链表,一个相同的结点即为交点,需要注意的是哈希表存放的是各个结点的地址,而非结点的值。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* a = headA;
ListNode* b = headB;
set<ListNode* > myset;
while(a) {
myset.insert(a);
a = a->next;
}
while (b) {
if (myset.find(b) != myset.end()) return b;
else b = b->next;
}
return nullptr;
}
};
解法二:双指针法
设置俩个指针分别指向俩个链表的表头,俩个指针同时向右遍历,当每个指针都走到表尾时再指向另一个链表的表头继续遍历,当俩个指针指向同一个结点时即为交点,若没有指向同一个结点,则返回空。
why?
因为若俩链表长度相同且有交点,则显然会再交换指向的表后指向交点。若长度不同则快的指针会先走完俩个链表长度的差值,达到从距离交点相同距离开始遍历的目的。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (headA == nullptr || headB == nullptr) {
return nullptr;
}
ListNode *pA = headA, *pB = headB;
while (pA != pB) {
pA = pA == nullptr ? headB : pA->next;
pB = pB == nullptr ? headA : pB->next;
}
return pA;
}
};
解法三:差值法
思路与解法二相同,均要达到从距离从距离交点相同距离的地方开始遍历的目的。先对两条链表扫描一遍,取得两者长度,然后让长的链表先走「两者的长度差值」,然后再同时走,遇到第一个节点即是答案。
解法四:栈方法
将俩个链表的结点值压栈,若最后一个值都不相同则显然不相交,若相同则不断取出俩个栈顶元素进行比较,第一个不同的元素的上一个元素即为交点。