一文读懂计算机视觉坐标系相机参数关系及相机标定

坐标系关系

世界坐标系(World Coordinate)

由于摄像机与被摄物体可以放置在环境中任意位置，这样就需要在环境中建立一个三维直角坐标系，来表示相机和被摄物体的位置，这个坐标系就称为世界坐标系

相机坐标系(Camera Coordinate)

相机坐标系也是一个三维直角坐标系，原点位于镜头光心处，X，Y轴分别与像平面的两边平行，Z轴为镜头光轴，与像平面垂直

世界坐标系到相机坐标系变换关系

旋转

绕X轴旋转，即X轴不变：

$\mathrm{R}(X_W,\psi )=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\psi & -sin\psi \\ 0& sin\psi & cos\psi \end{array}\right]$

绕Y轴旋转，即Y轴不变：

$\mathrm{R}(Y_W,\theta )=\left[\begin{array}{ccc}cos\theta & 0& sin\theta \\ 0& 1& 0\\ -sin\theta & 0& cos\theta \end{array}\right]$

绕Z轴旋转，即Z轴不变：

$\mathrm{R}(Z_W,\varphi )=\left[\begin{array}{ccc}cos\varphi & -sin\varphi & 0\\ sin\varphi & cos\varphi & 0\\ 0& 0& 1\end{array}\right]$

然后我们把绕三个轴旋转的矩阵进行相乘:

$\mathrm{R}=\mathrm{R}(Z_W,\varphi )\mathrm{R}(Y_W,\theta )\mathrm{R}(X_W,\psi )$

$\mathrm{R}=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$

平移

$\mathrm{t}=\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]$

变换公式以及相机外参(Extrinsics)

$\left[\begin{array}{c}{X}_C\\ Y_C\\ Z_C\end{array}\right]=\mathrm{R}\left[\begin{array}{c}{X}_W\\ Y_W\\ Z_W\end{array}\right]+\mathrm{t}$

写成齐次性矩阵：

$\left[\begin{array}{c}{X}_C\\ Y_C\\ Z_C\\ 1\end{array}\right]=\left[\begin{array}{cc}\mathrm{R}& t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_W\\ Y_W\\ Z_W\\ 1\end{array}\right]$

这样的目的是可以把坐标整合起来，变换矩阵第二行$\left[\begin{array}{cc}0& 1\end{array}\right]$ 是为了让世界坐标系和相机坐标系统一为4维表示。

写到这里，我们就得到了相机外参(Camera Extrinsics) $\mathrm{R},\mathrm{t}$

Q&A

Q: 为啥要把世界坐标系变到相机坐标系？
A: 因为我们的相机坐标系可以将世界点与图像联系起来

Q: 什么是世界点？
A: 一般情况下，我们是需要测量物体的距离和位置关系，因此世界坐标系一般定在相机工作的场景中

Q: 世界坐标系与相机坐标系的关系是什么？
A: 相机外参R,t

像素坐标系

像素坐标系UOV(u,v)是一个二维直角坐标系，反映了相机CCD/CMOS芯片中像素的排列情况。原点o位于图像的左上角，u轴，v轴分别与像平面的两边平行。像素坐标系中坐标轴的单位是像素(整数)。

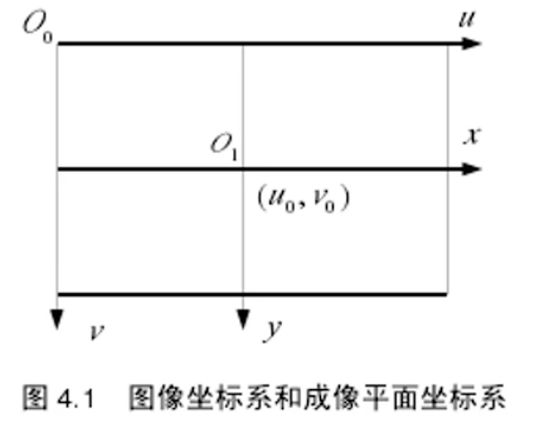
图像坐标系

像素坐标系不利于坐标变换，因此需要建立图像坐标系XOY(x,y)也是一个二维直角坐标系。其坐标轴的单位通常为毫米(mm)，原点是相机光轴与像平面的交点(称为主点)，即图像的中心点。x轴，y轴分别与u轴，v轴平行，故两个坐标系实际上是平移关系，即可以通过平移就可以得到。

图像坐标系到像素坐标系变换关系

$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{dX}& 0& u_0\\ 0& \frac{1}{dY}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$

其中，$dX$、$dY$分别是像素在X，Y轴方向上的物理尺寸，通俗点说就是X，Y轴上一个像素单位(cell size)对应着图像坐标系上的长度(单位是mm)，($u_0$，$v_0$)为主点（图像坐标系的原点）在像素坐标系上的坐标。

如果还不够清晰的话，我们把矩阵乘法按行展开，可以得到
$$\{\begin{array}{rl}u& =\frac{x}{dX}+u_0\\ y& =\frac{y}{dY}+v_0\\ 1& =1\end{array}$$
这样我们可以看到图像坐标系到像素坐标系变换关系其实就是一个伸缩+平移变换。

相机坐标系到图像坐标系变换关系

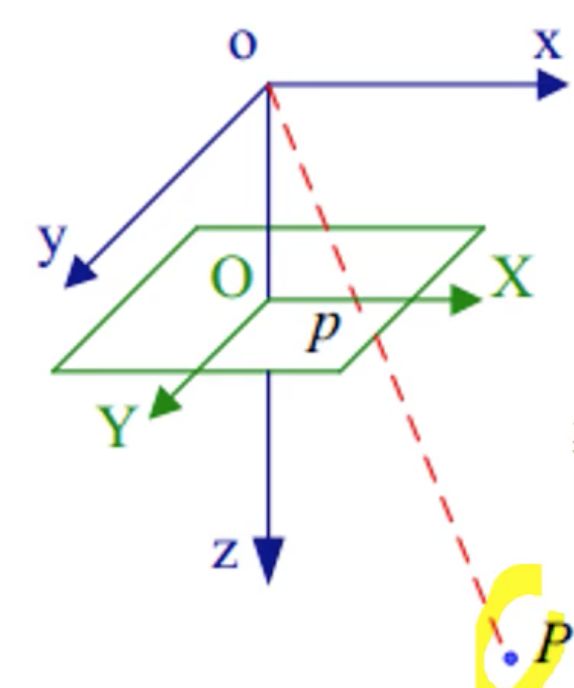
空间中任意一点$\mathrm{P}$，点$\mathrm{P}$在相机坐标系(Camera Coordinate) (图中的蓝色坐标系)中的坐标为($X_C$,$Y_C$,$Z_C$)，连接点$\mathrm{P}$与相机光心$o$的连线为$o\mathrm{P}$，$o\mathrm{P}$与像平面的交点为$p$，这个点$p$就是空间点$\mathrm{P}$拍照出来对应的像平面上的投影，点$p$在图像坐标系(图中的绿色坐标系)中的坐标为($x$,$y$)。该过程为透视投影，计算方法由相似三角形关系得到如下变换矩阵

$s\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_C\\ Y_C\\ Z_C\\ 1\end{array}\right]$

其中，s为比例因子(s不为0)，它的值等于$Z_C$，f为有效焦距(光心到图像平面的距离) $oO$。
接下来我们推导一下这个变换矩阵怎么得到的，将矩阵每一行展开为三个等式
$$\{\begin{array}{rlrl}sx& =f{X}_C& ⟺\frac{x}{X_C}& =\frac{f}{s}\\ sy& =f{Y}_C& ⟺\frac{y}{Y_C}& =\frac{f}{s}\\ s& =Z_C& & \end{array}$$
到此，我们可以看出这个变换是基于$△oZP$的边长坐标相似关系得出。

世界坐标系到像素坐标系变换关系

变换公式

到目前为止，我们已经清晰推导了世界坐标系——>相机坐标系——>图像坐标系——>像素坐标系。那么想得到世界坐标系——>像素坐标系的公式，直接将上面三个变换过程集合到一起(即将三个变换矩阵相乘)。

$\begin{array}{rl}s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]& =\left[\begin{array}{ccc}\frac{1}{dX}& 0& u_0\\ 0& \frac{1}{dY}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}\mathrm{R}& t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_W\\ Y_W\\ Z_W\\ 1\end{array}\right]\\ & =\left[\begin{array}{cccc}{\alpha }_x& 0& u_0& 0\\ 0& {\alpha }_y& v_0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}\mathrm{R}& t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_W\\ Y_W\\ Z_W\\ 1\end{array}\right]\\ & ={\mathrm{M}}_1{\mathrm{M}}_{2}V\\ & =\mathrm{M}V\end{array}$

尺度因子

${\alpha }_x=\frac{f}{dX}$、${\alpha }_y=\frac{f}{dY}$称为$u$、$v$轴的尺度因子

相机内参(Intrinsics)

${\mathrm{M}}_1=\left[\begin{array}{cccc}{\alpha }_x& 0& u_0& 0\\ 0& {\alpha }_y& v_0& 0\\ 0& 0& 1& 0\end{array}\right]$称为相机的内部参数矩阵

相机外参(Extrinsics)

${\mathrm{M}}_2=\left[\begin{array}{cc}\mathrm{R}& t\\ 0& 1\end{array}\right]$称为相机的外部参数矩阵

投影矩阵

$\mathrm{M}$= ${\mathrm{M}}_1$${\mathrm{M}}_2$ 称为投影矩阵

畸变系数(Distortion Parameter)

在几何光学和阴极射线管(CRT)显示中，畸变(Distortion) 也是对直线投影(Rectilinear Projection) 的一种偏移。简单来说，直线投影是场景内的一条直线投影到图片上也保持为一条直线，那畸变简单来说就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变(Optical Aberration)。

畸变一般分为两大类，包括径向畸变(Radial Distortion)和切向畸变，径向畸变来自透镜形状，切向畸变来自整个摄像机的组装过程。畸变还有其他类型的畸变，但没有径向畸变和切向畸变这么显著。

径向畸变(Radial Distortion)

实际摄像机的透镜，总是在成像仪的边缘产生显著的畸变，这种现象来源于透镜形状“筒形”或“鱼眼”的影响。光现在远离透镜中心的地方更加弯曲，光学中心的畸变为0。

桶形畸变(Barrel Distortion)

枕形畸变(Pincushion Distortion)

胡子畸变(Mustache Distortion)

切向畸变(Tangential Distortion)

切向畸变是由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的

薄透镜畸变(Thin Lens Distortion)

离心畸变(Centrifugal Distortion)

畸变矫正

既然有畸变，就需要对畸变进行矫正

径向畸变矫正公式

$x_{corr}=x_{dis}(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$
$y_{corr}=y_{dis}(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$

其中，$x_{dis}$，$y_{dis}$表示有畸变的坐标，$x_{corr}$，$y_{corr}$表示修复后的坐标，$k_1$，$k_2$，$k_3$表示径向畸变参数，r是跟相机径向相关的一个值

切向畸变矫正公式

$x_{corr}=x_{dis}+[2p_{1}xy+p_2(r^2+2x^2)]$
$y_{corr}=y_{dis}+[p_1(r^2+2y^2)+2p_{2}xy]$

其中，$x_{dis}$，$y_{dis}$表示有畸变的坐标，$x_{corr}$，$y_{corr}$表示修复后的坐标，$p_1$，$p_2$表示切向畸变系数，$x$，$y$是跟像素位置相关的值

畸变参数

那么，最终得到的5个畸变参数为
$$D=(k_1,k_2,k_3,p_1,p_2)$$

相机参数

经过以上讨论推导，对于一个单目相机而言，一共有16个相机参数

10个相机内部参数[只与相机内部结构有关]

5个内部矩阵参数K

$$K=(f,dx,dy,u_0,v_0)$$

5个畸变参数D

$$D=(k_1,k_2,k_3,p_1,p_2)$$

6个相机外部参数[与相机在世界坐标系下位置有关]

3个旋转参数R

$$R=(\psi ,\theta ,\varphi )$$

3个平移参数T

$$t=(t_x,t_y,t_z)$$

相机标定

目的

给定物体的参考点坐标$(x,y,z)$和它的像素坐标$(u,v)$,确定相机内部的几何和光学特性(相机内部参数)以及相机坐标系与世界坐标系关系(相机外部参数)

标定方法分类

传统的相机标定方法

在一定相机模型下，基于特定的实验条件，如形状、尺寸已知的参考物，进行图像处理、数学变换、技术方法，求取相机内外参数。包括利用最优化算法的标定方法，利用相机变换矩阵的标定方法，进一步考虑畸变补偿的两步法、张正友标定法。

张正友标定法

假设标定棋盘位于世界坐标系中$Z_W=0$平面，

$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& \gamma & u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{r}_1& r_2& t\end{array}\right]\left[\begin{array}{c}{X}_W\\ Y_W\\ 1\end{array}\right]$

其中$\gamma$是径向畸变系数

单应性变换(Homography)

来描述物体在世界坐标系和像素坐标系之间的位置映射关系。对应的变换矩阵称为单应性变换。单应性矩阵定义为

$H=\left[\begin{array}{ccc}{f}_x& \gamma & u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{r}_1& r_2& t\end{array}\right]$

其中，$H$为一个3*3的矩阵，并且有一个元素作为齐次坐标。因此，H有8个自由度。现在有8个自由度需要求解，所以需要四个对应点。也就是四个点就可以求出图像平面到世界平面的单应性矩阵H。

自标定法

这是一种不依赖参考物的标定方法，利用相机本身参数之间的约束关系来标定，利用周围图像与图像之间的对应关系，与场景和相机运动无关。基于Krupa方程、分层逐步标定法、基于二次曲面自标定法。