最小生成树（克鲁斯卡尔算法）

最小生成树：含有图中全部顶点，但只有足以构成一棵树的n - 1条边的连通子图，并且该连通子图所有边上的权值之和最小。

克鲁斯卡尔算法：将邻接矩阵转换成边集数组后，把边集数组按权值进行升序排序，之后使用循环从边集数组中取出第n小的边，并判断该边与已加入生成树的边是否生成回路，如果不生成回路则输出该边，边把该边加入生成树中，直到遍历完所有的边为止。

实现代码如下：

// 最小生成树（克鲁斯卡尔算法）
#include 

#define MAXVEX 20 // 最大顶点数
#define MAXEDGE 20 // 最大边数
#define INFINITY 65535 // 无穷

typedef int EdgeType; // 边上的权值类型

// 邻接矩阵结构
typedef struct {
    EdgeType arc[MAXVEX][MAXVEX]; // 边表
    int numNodes, numEdges; // 图中当前的顶点数，边数
}MGraph;

// 边集数组节点
typedef struct {
    int begin; // 边的起点
    int end; // 边的终点
    int weight; // 边的权值
} Edge;

/**
 * 生成邻接矩阵
 * @param G 邻接矩阵
 */
void CreateMGraph(MGraph *G) {
    int i, j; // 用于遍历元素

    G->numEdges = 15; // 设置有15条边
    G->numNodes = 9; // 设置有9个顶点

    // 初始化图的边
    for (i = 0; i < G->numNodes; i++) {
        for (j = 0; j < G->numNodes; j++) {
            if (i == j) { // 对角线边的值设置为0
                G->arc[i][j] = 0;
            } else { // 其他位置的边设置为无穷
                G->arc[i][j] = G->arc[j][i] = INFINITY;
            }
        }
    }

    // 设置特定边的权
    G->arc[0][1] = 10;
    G->arc[0][5] = 11;

    G->arc[1][2] = 18;
    G->arc[1][8] = 12;
    G->arc[1][6] = 16;

    G->arc[2][8] = 8;
    G->arc[2][3] = 22;

    G->arc[3][8] = 21;
    G->arc[3][6] = 24;
    G->arc[3][7] = 16;
    G->arc[3][4] = 20;

    G->arc[4][7] = 7;
    G->arc[4][5] = 26;

    G->arc[5][6] = 17;

    G->arc[6][7] = 19;

    // 设置对称边的权
    for (i = 0; i < G->numNodes; i++) {
        for (j = i; j < G->numNodes; j++) {
            G->arc[j][i] = G->arc[i][j];
        }
    }
}

/**
 * 交换边集数组节点中i和j位置的权值，以及起点和终点
 * @param edges 边集数组节点
 * @param i 下标
 * @param j 下标
 */
void Swapn(Edge *edges, int i, int j) {
    int temp; // 用于交换的临时变量
    
    // 交换i和j位置的起点
    temp = edges[i].begin;
    edges[i].begin = edges[j].begin; 
    edges[j].begin = temp;
    
    // 交换i和j位置的终点
    temp = edges[i].end;
    edges[i].end = edges[j].end;
    edges[j].end = temp;

    // 交换i和j位置的权值
    temp = edges[i].weight;
    edges[i].weight = edges[j].weight;
    edges[j].weight = temp;
}

/**
 * 对边集数组的权值进行排序
 * @param edges 边集数组
 * @param G 邻接矩阵
 */
void sort(Edge edges[], MGraph *G) {
    int i, j; // 用来遍历元素

    // 使用冒泡排序对边集数组进行排序
    for (i = 0; i < G->numEdges; i++) {
        for (j = i + 1; j < G->numEdges; j++) {
            // 前面节点比后面节点的权值大
            if (edges[i].weight > edges[j].weight) {
                // 交换节点i和节点j
                Swapn(edges, i, j);
            }
        }
    }

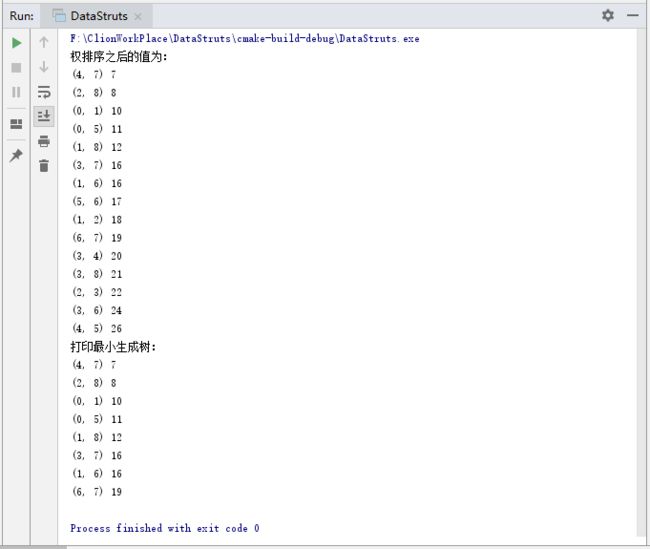
    printf("权排序之后的值为：\n");
    for (i = 0; i < G->numEdges; i++) {
        printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
    }
}

/**
 * 查找连线顶点的尾部下标
 * @param parent 判断边与边是否形成环路的数组
 * @param f 顶点下标
 * @return 边与边是否形成环路的数组
 */
int Find(int *parent, int f) {
    // 当parent[f]不为0时，表示该边与其他边相连，
    // 一直顺着相连的边直到一条不与其他边相连的边（parent[f] = 0）
    // 返回该边的顶点下标
    while (parent[f] > 0) {
        f = parent[f];
    }
    return f;
}

/**
 * 使用Kruskal算法生成最小生成树
 * @param G 邻接矩阵
 */
void MiniSpanTree_Kruskal(MGraph G) {
    int i, j, m, n; // i和j用来遍历元素，m和n用来获取
    int k = 0; // 用来遍历边集数组的下标
    int parent[MAXVEX]; // 判断边与边是否形成环路的数组
    Edge edges[MAXEDGE]; // 边集数组

    // 使用邻接矩阵来构建边集数组
    for (i = 0; i < G.numNodes - 1; i++) {
        for (j = i + 1; j < G.numNodes; j++) {
            if (G.arc[i][j] < INFINITY) {
                edges[k].begin = i; // 设置边集数组节点的起点
                edges[k].end = j; // 设置节点的终点
                edges[k].weight = G.arc[i][j]; // 设置节点的权值
                k++; // 用来遍历边集数组
            }
        }
    }

    sort(edges, &G); // 对边集数组的权值进行排序

    // 初始化判断边与边是否形成环路的数组
    for (i = 0; i < G.numNodes; i++) {
        parent[i] = 0; // 设置数据中所有值都为0
    }

    printf("打印最小生成树：\n");
    // 循环每一条边
    for (i = 0; i < G.numEdges; i++) {
        n = Find(parent, edges[i].begin); // 获取与该顶点相连最后一个顶点的下标
        m = Find(parent, edges[i].end);

        // n和m不相等，说明此边没有和现有生成树形成环路
        if (n != m) {
            parent[n] = m; // 将此边的结尾顶点放入parent数组，表示此顶点已经在生成树集合中

            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }

}

int main() {
    MGraph G; // 邻接矩阵
    CreateMGraph(&G); // 创建邻接矩阵
    MiniSpanTree_Kruskal(G); // Kruskal算法生成最小生成树

    return 0;
}

运行结果