2017年第八届蓝桥杯【省赛C/C++ A组】做题记录（附详细思路）

T1：迷宫

  X星球的一处迷宫游乐场建在某个小山坡上。它是由10x10相互连通的小房间组成的。房间的地板上写着一个很大的字母。我们假设玩家是面朝上坡的方向站立，则：L表示走到左边的房间，R表示走到右边的房间，U表示走到上坡方向的房间，D表示走到下坡方向的房间。
  X星球的居民有点懒，不愿意费力思考。他们更喜欢玩运气类的游戏。这个游戏也是如此！开始的时候，直升机把100名玩家放入一个个小房间内。
  玩家一定要按照地上的字母移动。

迷宫地图如下：
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR

  请你计算一下，最后，有多少玩家会走出迷宫? 而不是在里边兜圈子。
  思路分析：首先搞清什么叫走出迷宫。走出迷宫就是指玩家能够走到左边界某一个L字母位置处，或者右边界某一个R字母处，或者上边界某一个U字母处，或者下边界某一个D字母处。很明显这是一道需要用到dfs的题。
  具体做法：从每一个位置出发进行深搜，若按照规则走遍了所有能走的方格但是还是没有走出去，表明无法走出迷宫，否则计数器加1。
代码：

#include
using namespace std;

int vis[10][10];
int s[10][10];
int sum=0;

bool judge(int x,int y) {
     
    if(x>=0&&x<10&&y>=0&&y<10) {
     
    	return false;
	}
    return true;   //表明已经不再区域内，即成功走出迷宫 
}

void dfs(int x,int y) {
     
    if(judge(x,y)) {
       //走出迷宫 
        sum++;
        return;
    }
    if(!vis[x][y]) {
     
        vis[x][y]=1;
        if(s[x][y]=='U'){
     
        	dfs(x-1,y);
		}else if(s[x][y]=='D') {
     
		    dfs(x+1,y);	
		}else if(s[x][y]=='R') {
     
			dfs(x,y+1);
		}else if(s[x][y]=='L') {
     
			dfs(x,y-1);
		}
    }
}

int main() {
     
	int ct=0;
	string str="UDDLUULRULUURLLLRRRURRUURLDLRDRUDDDDUUUUURUDLLRRUUDURLRLDLRLULLURLLRDURDLULLRDDDUUDDUDUDLLULRDLUURRR";
	for(int i=0;i<10;i++) {
        //先分成而二维数组 
		for(int j=0;j<10;j++) {
     
			s[i][j]=str[ct];
			ct++;
		}
	}
	for(int i=0;i<10;i++) {
     
		for(int j=0;j<10;j++) {
     
			memset(vis,0,sizeof(vis));   //注意每一次深搜后都要重新将vis数组清零 
			dfs(i,j);
		}
	}
	cout<<sum;
	return 0; 
 } 

答案：31

T2：跳蚱蜢

如下图所示：

  有9只盘子，排成1个圆圈。其中8只盘子内装着8只蚱蜢，有一个是空盘。
  我们把这些蚱蜢顺时针编号为 1~8，每只蚱蜢都可以跳到相邻的空盘中，也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，并且保持空盘的位置不变（也就是1-8换位，2-7换位,…），至少要经过多少次跳跃？
注意：要求提交的是一个整数，请不要填写任何多余内容或说明文字。

具体见：【跳蚱蜢】2017年第八届蓝桥杯【C/C++省赛A组】

T3：魔方状态

  二阶魔方就是只有2层的魔方，只由8个小块组成。如下所示：

  小明很淘气，他只喜欢3种颜色，所有把家里的二阶魔方重新涂了颜色，如下：

前面：橙色
右面：绿色
上面：黄色
左面：绿色
下面：橙色
后面：黄色

  请你计算一下，这样的魔方被打乱后，一共有多少种不同的状态。
  如果两个状态经过魔方的整体旋转后，各个面的颜色都一致，则认为是同一状态。
  请提交表示状态数的整数，不要填写任何多余内容或说明文字。

  思路分析：暂时没有好的思路。

T4：方格分割

  6x6的方格，沿着格子的边线剪开成两部分，要求这两部分的形状完全相同。如图：p1.png, p2.png就是可行的分割法。


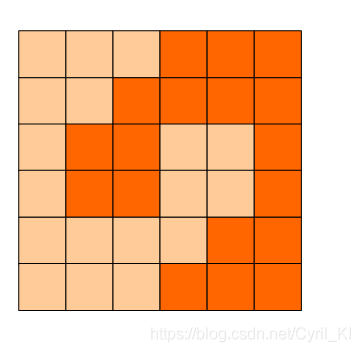
  试计算：包括这2种分法在内，一共有多少种不同的分割方法。
  注意：旋转对称的属于同一种分割法。请提交该整数，不要填写任何多余的内容或说明文字。

  思路分析：这道题刚开始也没有找到好的思路，以为也是那种需要暴力搜索的题，后来查了查资料才恍然大悟。我们记中心点坐标为（3,3），从中心点开始走：

  从上图可以看出，如果我们一个箭头往上走，那么另一个箭头就往下走；一个箭头向右走则另一个箭头向左走。当一个箭头碰到边界时另一个箭头也就碰到了边界，此时二者所走过的边界就是一个可行解。
  因此思路就变得非常清晰了：DFS。最后，由于对称性，比如将上图分别旋转90,180,270,360度之后得到的四种可能，实际上是一种可能！！因此最后答案要除以4。
代码：

#include
using namespace std;
 
int dir[4][2] = {
     0,1, 0,-1, 1,0, -1,0};  //四个方向 
bool vis[9][9];
int ans = 0;

void dfs(int x, int y){
     
	if(x == 0 || y == 0 || x == 6 || y == 6){
        //找到边界，分割完成 
		ans++;
		return ;
	}
	for(int i = 0; i < 4; i++){
     
		int x1 = x + dir[i][0];
		int y1 = y + dir[i][1];
		int x2 = 6 - x1;
		int y2 = 6 - y1;
		if(x1 >= 0 && y1 >= 0 && x1 <= 6 && y1 <= 6){
     
			if(!vis[x1][y1]){
     
				vis[x1][y1] = vis[x2][y2] = true;
				dfs(x1,y1);
				vis[x1][y1] = vis[x2][y2] = false;  //回溯 
			}
		}
	}
}
 
int main(){
     
	memset(vis, false, sizeof(vis));
	vis[3][3] = 1;
	dfs(3,3);
	cout<<ans/4;
	return 0;
}

答案：509

T5：字母组串

  由 A,B,C 这3个字母就可以组成许多串。比如：“A”,“AB”,“ABC”,“ABA”,“AACBB” …
  现在，小明正在思考一个问题：如果每个字母的个数有限定，能组成多少个已知长度的串呢？
  他请好朋友来帮忙，很快得到了代码，解决方案超级简单，然而最重要的部分却语焉不详。请仔细分析源码，填写划线部分缺少的内容。

#include
using namespace std;
// a个A，b个B，c个C 字母，能组成多少个不同的长度为n的串。
int f(int a, int b, int c, int n)
{
     
	if(a<0 || b<0 || c<0) return 0;
	if(n==0) return 1; 
	
	return f(a,b,c-1,n-1)+f(a-1,b,c,n-1)+f(a,b-1,c,n-1);  // 填空
}

int main()
{
     
	printf("%d\n", f(1,1,1,2));
	printf("%d\n", f(1,2,3,3));
	return 0;
}

  思路分析：刚开始a，b，c肯定是大于0的，递归出口是三者之一小于0，因此return 后面递归调用时a，b，c肯定都是比原来小的。我们再根据题意，要组成长度为n的串，假设我减少一个a，那么长度就变成了n-1，减少b，c是一样的，因此最终答案为：
答案：f(a,b,c-1,n-1)+f(a-1,b,c,n-1)+f(a,b-1,c,n-1);

T6：最大公共子串

  最大公共子串长度问题就是：求两个串的所有子串中能够匹配上的最大长度是多少。
  比如：“abcdkkk” 和 “baabcdadabc”，可以找到的最长的公共子串是"abcd",所以最大公共子串长度为4。
  下面的程序是采用矩阵法进行求解的，这对串的规模不大的情况还是比较有效的解法。
  请分析该解法的思路，并补全划线部分缺失的代码。

#include 
#include 

#define N 256
int f(const char* s1, const char* s2) {
     
	int a[N][N];
	int len1 = strlen(s1);
	int len2 = strlen(s2);
	int i,j;
	
	memset(a,0,sizeof(int)*N*N);
	int max = 0;
	for(i=1; i<=len1; i++){
     
		for(j=1; j<=len2; j++){
     
			if(s1[i-1]==s2[j-1]) {
     
				a[i][j] = a[i-1][j-1]+1;  //填空
				if(a[i][j] > max) max = a[i][j];
			}
		}
	}
	
	return max;
}

int main() {
     
	printf("%d\n", f("abcdkkk", "acbdchd"));
	return 0;
}

  思路分析：：最长公共子序列、最长公共子串的输出

T7：正则问题

  考虑一种简单的正则表达式：只由 x ( ) | 组成的正则表达式。
小明想求出这个正则表达式能接受的最长字符串的长度。
  例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是： xxxxxx，长度是6。
  输入：一个由x()|组成的正则表达式。输入长度不超过100，保证合法。
  输出：这个正则表达式能接受的最长字符串的长度。
  例如，输入：((xx|xxx)x|(x|xx))xx ，程序应该输出：6

  思路分析：说实话刚开始我没搞懂这个题目是什么意思。。。。后来仔细想了想才想明白。正则表达式里面的 ‘|’ 是或的意思，就拿上面的例子举例：((xx|xxx)x|(x|xx))xx：
  两个x和三个x或运算二选一，要使得最后长度最大，我们理应选择三个x，三个x与相邻的x组成四个x，右边括号内选择两个x，两个x与前面的四个x或运算我们选择四个x，最后再与最外面的两个x组成六个x，即是最终答案。

  思路分析：从上图可以看出，我们是将该正则表达式分段处理，然后拼凑在一起，有点递归的味道在里面，因此这里我们也还是首先想到递归解法。
  我们从头到尾遍历这个正则表达式，如果遇到了左括号，那我们就要等待遇到右括号，在遍历的时候我们要用一个中间变量temp来保存当前括号开始的x长度；如果遇到右括号表明当前段的运算已经结束；如果遇到’|’，表明我们就要做出抉择。

#include
using namespace std;
char s[105];
int index=0;

//((xx|xxx)x|(x|xx))xx为6

int f() {
     
    int maxn=0;
    int temp=0;
    while(index<strlen(s)) {
     
        if(s[index]=='(') {
     
            index++;
            temp+=f();//统计一对括号中X的最大值返回之后将它记录到当前括号中
           }
        else if(s[index]==')') {
     
            index++;
            break;
        }
        else if(s[index]=='|') {
     
            index++;
            if(temp>maxn) {
     
            	maxn=temp; //做出抉择
			} 
            temp=0; // 重新计数
        }
        else {
     
            temp++;
            index++;
        }
    }
    if(temp>maxn) maxn=temp;
    return maxn;
}
int main() {
       
    scanf("%s",s);
    cout<<f()<<endl;
    return 0;
}

T8：包子凑数

  小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼，其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼，可以认为是无限笼。
  每当有顾客想买X个包子，卖包子的大叔就会迅速选出若干笼包子来，使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼，分别能放3、4和5个包子。当顾客想买11个包子时，大叔就会选2笼3个的再加1笼5个的（也可能选出1笼3个的再加2笼4个的）。
  当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼，分别能放4、5和6个包子。而顾客想买7个包子时，大叔就凑不出来了。
  小明想知道一共有多少种数目是包子大叔凑不出来的。

输入

第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)

输出

一个整数代表答案。如果凑不出的数目有无限多个，输出INF。

例如，输入：
2
4
5

程序应该输出：
6

再例如，输入：
2
4
6

程序应该输出：
INF

样例解释：
对于样例1，凑不出的数目包括：1, 2, 3, 6, 7, 11。
对于样例2，所有奇数都凑不出来，所以有无限多个。

  思路分析：这道题的大概意思是解一个方程，即：
  根据代数知识我们很容易知道，只有当$A_1，A_2，A_3...A_N$互质时上述方程才有解。因此我们第一步要做的就是判断所有系数是否互质，判断方法就是去求两两之间的最大公约数，若不是1，则表示无解，输出INF，否则我们定义一个数组dp，dp[i]代表拿i个包子是否可能,1表示可能，0表示不可能。假设dp[j]=1，那么很显然dp[j+A[i]]=1，我们只要再拿一笼A[i]个数的包子就行。

#include
using namespace std;

const int maxn=1e5;
int dp[maxn], a[105];//dp[i]代表拿i个包子是否可能,1表示可能，0表示不可能 

int gcd(int a, int b) {
     
	return b?gcd(b,a%b):a;
}
int main() {
     
	int n, g, num = 0;
	cin>>n;
	for (int i = 0; i < n; i++) {
     
		cin >> a[i];
	}
	g = gcd(a[0], a[1]);
	for (int i = 2; i < n; i++) {
     
		g = gcd(g, a[i]);
	}//两两求最大公因子
	if (g != 1) cout << "INF" << endl;   //不互质，则有无限种都不能表示 
	else {
     
		dp[0] = 1;//0个包子肯定可以
		for (int i = 0; i < n; i++) {
     
			for (int j = 0; j +a[i]< maxn; j++) {
     
				if (dp[j]) {
     
					dp[j + a[i]] = 1;
				}
			}
		}
		for (int i = 0; i < maxn; i++) {
     
			if(!dp[i]) {
     
				num++;
			}
		}
		cout << num << endl;
	}
	return 0;
}

T9：分巧克力

  儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
  小明一共有N块巧克力，其中第i块是Hi x Wi的方格组成的长方形。
  为了公平起见，小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足：

1. 形状是正方形，边长是整数
2. 大小相同

  例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。
  当然小朋友们都希望得到的巧克力尽可能大，你能帮小Hi计算出最大的边长是多少么？

输入：
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。

输出：
输出切出的正方形巧克力最大可能的边长。

样例输入：
2 10
6 5
5 6

样例输出：
2
  思路分析：【分巧克力】2017年第八届蓝桥杯【C/C++省赛A组】

T10：油漆面积

  X星球的一批考古机器人正在一片废墟上考古。该区域的地面坚硬如石、平整如镜。管理人员为方便，建立了标准的直角坐标系。
  每个机器人都各有特长、身怀绝技。它们感兴趣的内容也不相同。
  经过各种测量，每个机器人都会报告一个或多个矩形区域，作为优先考古的区域。
  矩形的表示格式为(x1,y1,x2,y2)，代表矩形的两个对角点坐标。
  为了醒目，总部要求对所有机器人选中的矩形区域涂黄色油漆。小明并不需要当油漆工，只是他需要计算一下，一共要耗费多少油漆。
  其实这也不难，只要算出所有矩形覆盖的区域一共有多大面积就可以了。
  注意，各个矩形间可能重叠。

本题的输入为若干矩形，要求输出其覆盖的总面积。

输入格式：
第一行，一个整数n，表示有多少个矩形(1<=n<10000)
接下来的n行，每行有4个整数x1 y1 x2 y2，空格分开，表示矩形的两个对角顶点坐标。
(0<= x1,y1,x2,y2 <=10000)

输出格式：
一行一个整数，表示矩形覆盖的总面积。

例如，
输入：
3
1 5 10 10
3 1 20 20
2 7 15 17

程序应该输出：
340

再例如，
输入：
3
5 2 10 6
2 7 12 10
8 1 15 15

程序应该输出：
128

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 2000ms
  思路分析：看到这题，首先想到了以前做的关于容斥原理的笔记：

感觉好像差不了太多，都是一个意思，有重复覆盖，最后让我们求覆盖面积，但其实好像没有太大关系。。。
  换一种思路：我们不管有没有覆盖，每次只要输入一个矩形，就将该矩形内的方格全部涂色，后面肯定会有重复的，我们依然涂色。最后遍历一下所有方格，只要涂色了，面积就加1，这是最暴力的解法，反正如果我在考场上我肯定会去这么做。这里要注意输入的坐标可能不是按照从小到大的顺序输入的，也就是说x1不一定小于x2。

#include
using namespace std;

const int maxn=1e4+5;
int ans=0,max1=0,max2=0;
bool vis[maxn][maxn];

int main() {
     
	int n,x1,y1,x2,y2;
	cin>>n;
	while(n--) {
     
		cin>>x1>>y1>>x2>>y2;
		int m=min(x1,x2),n=max(x1,x2);
		max1=max(max1,n);        //小小地优化一下 
		int p=min(y1,y2),q=max(y1,y2);
		max2=max(max2,q);
		for(int i=m;i<n;i++) {
     
			for(int j=p;j<q;j++) {
     
				vis[i][j]=1;
			}
		}
	}
	for(int i=0;i<max1;i++) {
     
		for(int j=0;j<max2;j++) {
     
			if(vis[i][j]) {
     
				ans++;
			}
		}
	}
	cout<<ans;
	return 0;
}