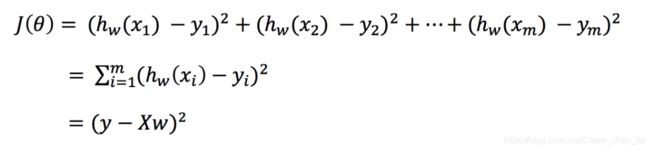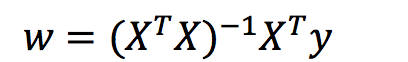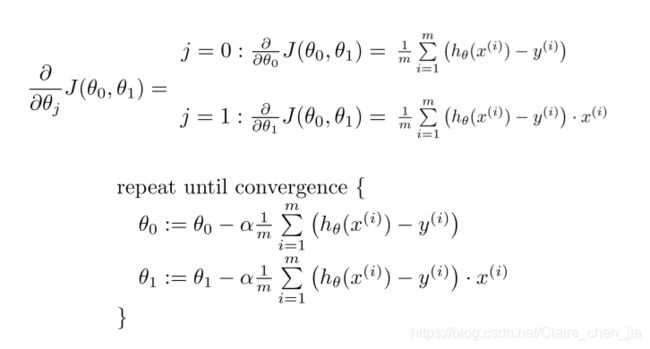python机器学习 | 线性回归-正规方程和梯度下降
今天看到一句话,“房间是生活的珠宝盒”,就感觉很精致,哈哈,终于找到一个高大上的死宅借口啦~
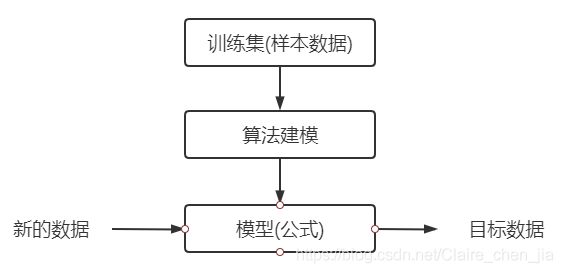
这篇博文主要讲得是线性回归,包括概念原理介绍,优化算法(正规方程和梯度下降),这里比较重要的是梯度下降
分享最近发现的宝藏:
- 梯度下降法详解+代码:批量梯度下降(BATCH GD)、小批量梯度下降(MINI-BATCH GD)、随机梯度下降(STOCHASTIC GD)
看了一下公号介绍,博主好像是校友 - 《动手学深度学习》(PyTorch版)
正规方程和梯度下降
- 1线性回归介绍
-
- 1.1 定义
- 1.2用途
- 1.3流程
- 1.4分类
- 1.5原理
- 1.6线性回归api
- 2优化算法之正规方程
-
- 2.1 介绍
- 2.2 评价
- 2.3 正规方程示例 -- 波士顿地区房价
- 3优化算法之梯度下降
-
- 3.1梯度下降介绍
- 3.2 评价
- 3.3 梯度下降原理代码实现
- 3.4 梯度下降示例 -- 波士顿地区房价
- 3.5 梯度下降的其他算法
- 3.6 正规方程和梯度下降的比较
- 4 多元线性回归
1线性回归介绍
1.1 定义
(1)定义:线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
1.2用途
(2)用途:利用现有数据,建立模型(线性模型),然后输入自变量(特征值),预测因变量(目标值)
1.3流程
1.4分类
(4)分类:根据自变量(特征值)的个数可划分为一元线性回归、多元线性回归,具体介绍如下
-
一元线性回归模型:
只有一个输入变量(自变量),即只有一个特征,输入后,预测的输出变量(h,因变量,目标)
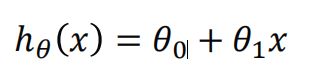
这个方程对应的图像是一条直线,称作回归线。其中, 1为回归线的斜率, 0为回归线的截距。 -
多元线性回归
与一元线性回归类似,只是输入变量变多了。理解为输入变量(自变量、特征时)有多个(即x=(x_1,x_2,…,x_n))时,预测的输出变量(h,因变量,目标)

1.5原理
(5)模型推测原理是基于损失函数中的损失最小,也就是预测目标值h和真实目标值y的距离最小,也就是损失最小。
下面就来介绍损失函数是个什么东东?
1)损失函数亦称为代价函数,它是以「均方误差」形式来衡量我们的假设函数的准确性。
2)公式
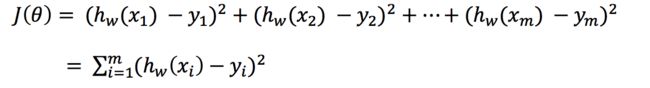
简化为:
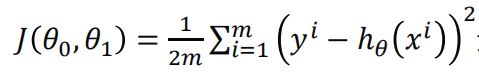
xi为第i个训练样本的特征集
yi为第i个训练样本的真实值
hθ(xi)为第i个训练样本特征值组合预测函数,也就是预测值
那么**(yi-hθ(xi))的平方** 代表的就是预测目标值和真实目标值之间的欧式距离,两点越近,代表训练结果越好。所有点距离平方之和除以样本数 m 就是均方误差。而再除以 2 是为了方便计算。
总的来说,代价函数值越小越好。所以从本质上讲,他就是通过求均方误差最小化来求解模型,所以也就是「最小二乘法OLS」。
那么求均方误差最小化,其实就是要算出θ(截距)和θ(斜率)值,而这就是优化算法需要做的事情(优化,做到总损失最小),其实就是数学里面的求偏导。
常用的优化算法就包括了正规方程和梯度下降两种方法,其中梯度下降在机器学习中应用更为广泛,这里也会深入介绍一下梯度下降
1.6线性回归api
下面简单举个例子,串一下线性回归的实现
(1)使用的模块是:
sklearn.linear_model.LinearRegression()
(2)数据大概如下:
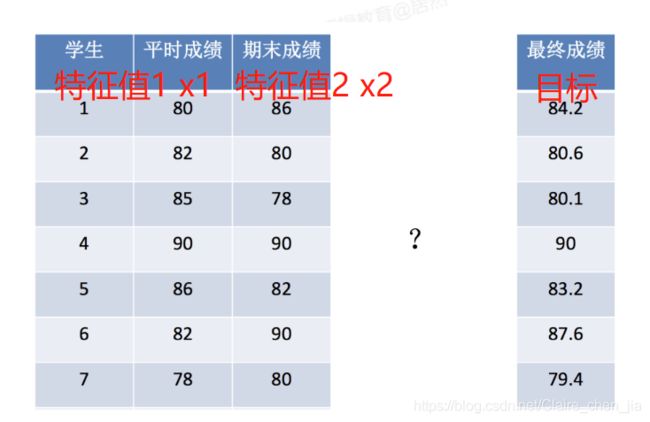
(3)步骤分析
• 1.获取数据集
• 2.数据基本处理
• 3.特征工程
• 4.机器学习(这里是线性回归)
• 5.模型评估
"""
步骤分析
• 1.获取数据集
• 2.数据基本处理
• 3.特征工程
• 4.机器学习(这里是线性回归)
• 5.模型评估
"""
# 导入模块
from sklearn.linear_model import LinearRegression # 线性回归模块
from sklearn.model_selection import train_test_split # 数据集分割模块
from sklearn.preprocessing import StandardScaler # 特征工程标准化模块
from sklearn.metrics import mean_squared_error # 模型评估
# 获取数据集
## 9个样本的特征值(二维)
x = [[80, 86],[82, 80],[85, 78],[90, 90],[86, 82],[82, 90],[78, 80],[92, 94]]
## 9个样本的目标值(连续型目标值)
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]
# 数据集的划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 特征工程
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_text = transfer.fit_transform(x_test)
# 线性回归
es = LinearRegression()
es.fit(x_train, y_train)
# 模型评估
y_pre = es.predict(x_test)
print("预测特征为:\n", x_test)
print("预测值:\n", y_pre)
print("模型中的系数:\n", es.coef_)
score = es.score(x_test, y_test)
print("准确率:\n", score)
# 均方误差
error = mean_squared_error(y_test, y_pre)
print("误差:\n", error)
"""
结果太不准了 ==
预测特征为:
[[82, 80], [90, 90]]
预测值:
[511.98784687 562.32619299]
模型中的系数:
[1.36839322 3.93912004]
准确率:
-9260.826777106246
误差:
204593.75350627722
"""
下面一个小节我详细介绍一下这两种优化算法,了解一下原理本质
2优化算法之正规方程
2.1 介绍
正规方程是直接求导得到θ最优值,一步到位。具体过程如下:
而对其求解关于w的最小值(最优解),由于y,X 均已知,所以二次函数直接求导,导数为零的位置,即为最小值。
2.2 评价
- 评价:由于其本质是直接求导。高中求导的时候,我们见到过一些函数是求不出导的,而且如果自变量一多,运算就慢。所以总的来说,当特征过多过复杂时,求解速度太慢并且得不到结果
2.3 正规方程示例 – 波士顿地区房价
美国波士顿地区房价数据为例
"""
1.获取数据
2.数据集划分
3.特征工程
4.线性回归(正规方程(LinearRegression)
5.模型评估
"""
from sklearn.datasets import load_boston # 导入数据集
from sklearn.model_selection import train_test_split # 数据分割
from sklearn.preprocessing import StandardScaler # 特征工程标准化
from sklearn.linear_model import LinearRegression # 正规方程模块
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 模型评估(拟合优度、均方差误)
def linear_model():
# 获取数据
data = load_boston()
# 数据集的划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)
# 特征工程
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_text = transfer.fit_transform(x_test)
# 线性回归(正规方程)
es = LinearRegression()
es.fit(x_train, y_train)
# 模型评估
y_pre = es.predict(x_test)
print("预测值:\n", y_pre)
print("模型中的系数:\n", es.coef_)
error1 = r2_score(y_test, y_pre) # 拟合优度
print("准确率:\n", error1)
error2 = mean_squared_error(y_test, y_pre) # 均方误差
print("误差1:\n", error2)
error3 = mean_absolute_error(y_test, y_pre) # 均方误差
print("误差2:\n", error3)
if __name__ == '__main__':
linear_model() # 准确率:-4380.439454836236
3优化算法之梯度下降
3.1梯度下降介绍
(1)梯度下降的整体理解:
梯度下降,我的理解是对损失函数的θ多次求偏导,迭代多次,从最陡峭的θ变化到倒数第一个θ和倒数第二个θ差不多,进而到达最优解。以场景示例来解释的话,梯度下降求解类似于下山:
假设一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方(最陡峭的方向就是求偏导),然后朝着山的高度下降的地方走,(同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走)。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
现在让我们来转换到梯度下降来:
首先,我们有一个可微分的函数。这个函数就代表着一座山,这个函数就是代价函数。那么我们的目标就是找到这个函数的最小值,也就是山底,也就是损失最小。
根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让损失函数的值下降的最快!因为梯度的方向就是函数之变化最快的方向。 所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。
其实正规方程就是一步到位,找到最最陡峭的方向(极端地讲可以说是跳到山谷),而梯度下降是慢慢摸索,一段一段来
(2)梯度解释:梯度是微积分中的概念。
- 在单变量的函数中(y=a+bx),梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率(b)。
- 在多变量函数(y=a+b1x1+b2x2+…)中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向。
3)这就是我们为什么要求梯度的原因,我们为了寻找最快到山谷,就需要在每一步观测到此时最陡峭的地方,而梯度就恰巧告诉了我们这个方向。
4)梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的反方向一直走,就能走到局部的最低点!而这也是梯度公式前面加负号的原因。
(3)梯度下降公式
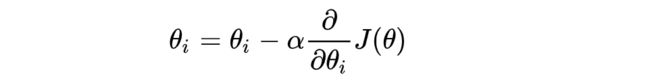
其中α是在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,α不应该过大也过小。
注意:
过大:容易错过了最低点!
过小:迟迟走不到最低点!
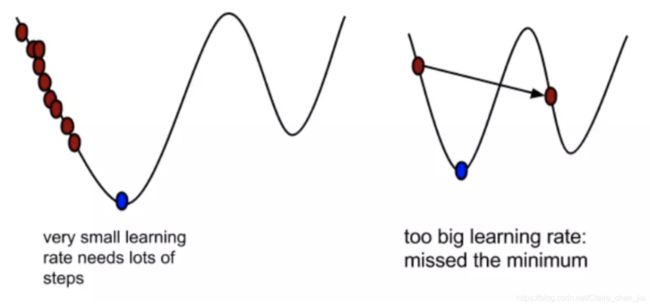
(5)举个演算的例子:
假设有一个单变量的函数(损失函数) :J(θ) = θ2 (这里是平方)
函数的微分:J·(θ) = 2θ
初始化,起点为: θ0 = 1(设初始值θ为1,这样由图可知,损失值最大现在)
学习率:α = 0.4(每一次买的步子)
我们开始进行梯度下降的迭代计算过程:
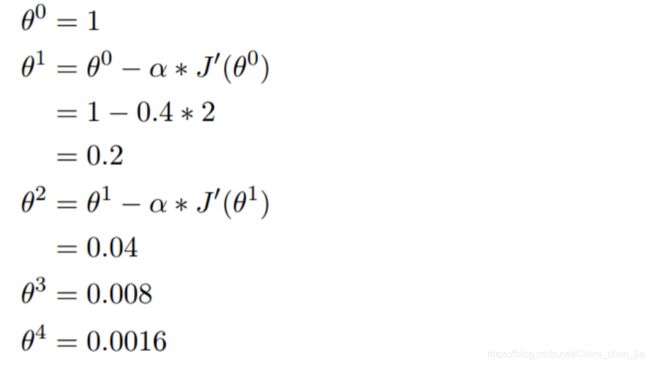
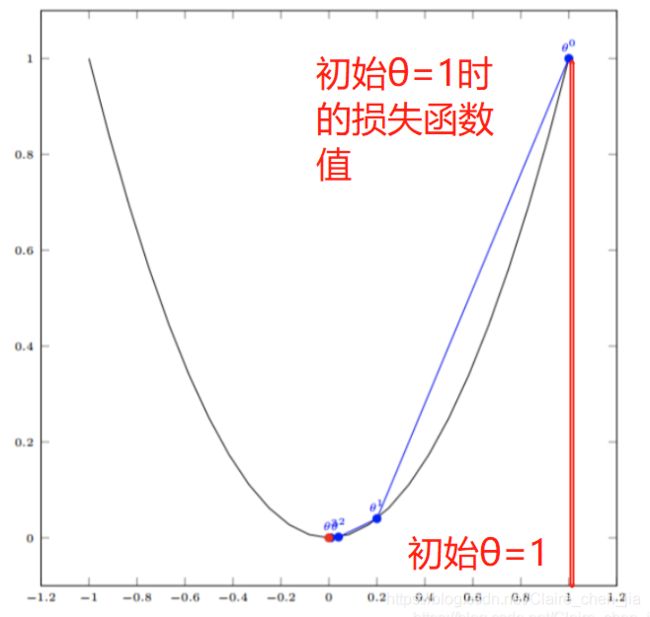
对代价函数求偏导数,就是求出该点的切线的斜率,它将为我们提供一个朝向的方向。我们在最陡下降的方向上降低代价函数,所以是迭代着递减下去。
而每个步骤的大小由参数 α 确定,该参数称为学习率。当梯度下降算法到达最小点(不管是局部还是全局)时,算法再也无法改变参数(因为导数为 0),此时即收敛。
3.2 评价
评价:因为达到局部或全局的时候,都会停止,收敛。这样可能导致算出的不是最优解。
如图:

3.3 梯度下降原理代码实现
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2020/11/5 14:37
# @Author : Claire
# @File : 梯度下降实现代码.py
# @Software: PyCharm
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
"""
这里以一元线性回归实现梯度下降
方程为 y = kX + b
"""
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
X = data[:,0] # 特征集
y = data[:,1] # 目标值
print(X,y)
plt.scatter(X,y)
plt.show()
# 设置迭代次数,学习率,初始θ值(k和b)
epochs = 50
lr = 0.0001 # 学习率
k = 0 # 斜率
b = 0 # 截距
# 最小二乘法 y = kX + b
def compute_error(b, k, X, y):
"""
计算损失函数的损失值
"""
totalError = 0
for i in range(0, len(X)):
# 真实值 - 预测值
totalError += (y[i] - (k * X[i] + b)) ** 2
return totalError / float(len(X)) / 2.0
def gradient_descent_runner(X, y, b, k, lr, epochs):
"""
梯度下降,不断优化θ,减少损失的过程
"""
# 计算总数据量
m = float(len(X))
# 循环epochs次
for i in range(epochs):
b_grad = 0
k_grad = 0
# 计算梯度的总和再求平均 这个算法计算梯度用的整个训练集
for j in range(0, len(X)):
b_grad += (1 / m) * (((k * X[j]) + b) - y[j])
k_grad += (1 / m) * X[j] * (((k * X[j]) + b) - y[j])
# 更新b和k
b = b - (lr * b_grad)
k = k - (lr * k_grad)
# 每迭代5次,输出一次图像
if i % 5 == 0:
print("epochs:", i)
plt.scatter(X, y)
plt.plot(X, k * X + b, 'r')
plt.show()
return b, k
print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, X, y)))
print("Running...")
b, k = gradient_descent_runner(X, y, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, X, y)))
3.4 梯度下降示例 – 波士顿地区房价
美国波士顿地区房价数据为例
"""
1.获取数据
2.数据集划分
3.特征工程
4.线性回归(梯度下降(SGDRegressor))
5.模型评估
"""
from sklearn.datasets import load_boston # 导入数据集
from sklearn.model_selection import train_test_split # 数据分割
from sklearn.preprocessing import StandardScaler # 特征工程标准化
from sklearn.linear_model import SGDRegressor # 梯度下降模块
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error # 模型评估(拟合优度、均方差误)
def SGDR_model():
# 获取数据
data = load_boston()
# 数据集的划分
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)
# 特征工程
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_text = transfer.fit_transform(x_test)
# 线性回归(梯度下降)
es = SGDRegressor()
es.fit(x_train, y_train)
# 模型评估
y_pre = es.predict(x_test)
print("预测值:\n", y_pre)
print("模型中的系数:\n", es.coef_)
error1 = r2_score(y_test, y_pre) # 拟合优度
print("准确率:\n", error1)
error2 = mean_squared_error(y_test, y_pre) # 均方误差
print("误差1:\n", error2)
error3 = mean_absolute_error(y_test, y_pre) # 均方误差
print("误差2:\n", error3)
if __name__ == '__main__':
linear_model() # 准确率:-4380.439454836236
SGDR_model() # 准确率:-789.2922797759195
3.5 梯度下降的其他算法
常见的梯度下降算法有:
- 全梯度下降算法(Full gradient descent),
- 随机梯度下降算法(Stochastic gradient descent),
- 随机平均梯度下降算法(Stochastic average gradient descent)
- 小批量梯度下降算法(Mini-batch gradient descent),
它们都是为了正确地调节权重向量,通过为每个权重计算一个梯度,从而更新权值,使目标函数尽可能最小化。其差别在于样本的使用方式不同。
(1)全梯度下降算法(FG)
就是我们上文介绍的方法,最基本的方法。
它是计算训练集所有样本误差,对其求和再取平均值作为梯度计算的目标函数。
在执行每次更新时,我们需要在整个数据集上计算所有的梯度,所以全梯度下降法的速度会很慢,同时,全梯度下降法无法处理超出内存容量限制的数据集。全梯度下降法同样也不能在线更新模型,即在运行的过程中,不能增加新的样本。
其是在整个训练数据集上计算损失函数关于参数θ的梯度:
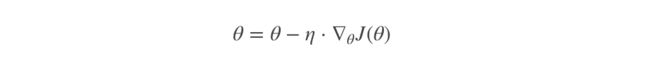
(2)随机梯度下降算法(SG)
全梯度下降的最要问题是计算每一步的梯度时都需要使用整个训练集,这导致在规模较大的数据集上,其会变得非常的慢。与其完全相反的随机梯度下降,在每一步的梯度计算上只随机选取训练集中的一个样本。很明显,由于每一次的操作都使用了非常少的数据,这样使得算法变得非常快。由于每一次迭代,只需要在内存中有一个实例,这使随机梯度算法可以在大规模训练集上使用。
另一方面,由于它的随机性,与批量梯度下降相比,其呈现出更多的不规律性:它到达最小 值不是平缓的下降,损失函数会忽高忽低,只是在大体上呈下降趋势。随着时间的推移,它 会非常的靠近最小值,但是它不会停止在一个值上,它会一直在这个值附近摆动。因此,当算法停止的时候,最后的参数还不错,但不是最优值。
但同时值得注意的是,SG每次只使用一个样本迭代,若遇上噪声则容易陷入局部最优解。
![]()
(3)小批量梯度下降算法(mini-batch)
小批量梯度下降算法是FG和SG的折中方案,在一定程度上兼顾了以上两种方法的优点。
每次从训练样本集上随机抽取一个小样本集,在抽出来的小样本集上采用FG迭代更新权重。
被抽出的小样本集所含样本点的个数称为batch_size,通常设置为2的幂次方,更有利于GPU加速处理。
特别的,若batch_size=1,则变成了SG;若batch_size=n,则变成了FG.其迭代形式为
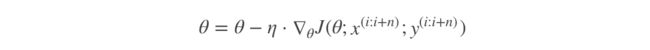
(4)随机平均梯度下降算法(SAG)
在SG方法中,虽然避开了运算成本大的问题,但对于大数据训练而言,SG效果常不尽如人意,因为每一轮梯度更新都完全与上一轮的数据和梯度无关。
随机平均梯度算法克服了这个问题,在内存中为每一个样本都维护一个旧的梯度,随机选择第i个样本来更新此样本的梯度,其他样本的梯度保持不变,然后求得所有梯度的平均值,进而更新了参数。
如此,每一轮更新仅需计算一个样本的梯度,计算成本等同于SG,但收敛速度快得多。
也就是对随机抽取的样本的梯度不清除掉,每次随机计算后,基于前面所有计算了的梯度求平均
对比总结
1)FG方法由于它每轮更新都要使用全体数据集,故花费的时间成本最多,内存存储最大。
2)SAG在训练初期表现不佳,优化速度较慢。这是因为我们常将初始梯度设为0,而SAG每轮梯度更新都结合了上一轮梯度值。
3)综合考虑迭代次数和运行时间,SG表现性能都很好,能在训练初期快速摆脱初始梯度值,快速将平均损失函数降到很低。但要注意,在使用SG方法时要慎重选择步长,否则容易错过最优解。
4)mini-batch结合了SG的“胆大”和FG的“心细”,从6幅图像来看,它的表现也正好居于SG和FG二者之间。在目前的机器学习领域,mini-batch是使用最多的梯度下降算法,正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点。
更多梯度下降算法的实现可以阅读: 梯度下降法详解+代码:批量梯度下降(BATCH GD)、小批量梯度下降(MINI-BATCH GD)、随机梯度下降(STOCHASTIC GD)
文章讲解得很清楚,也有示例!!!
3.6 正规方程和梯度下降的比较
4 多元线性回归
前面讲的都是以一元线性回归为例,最后再介绍一下多元线性回归。其实大同小异
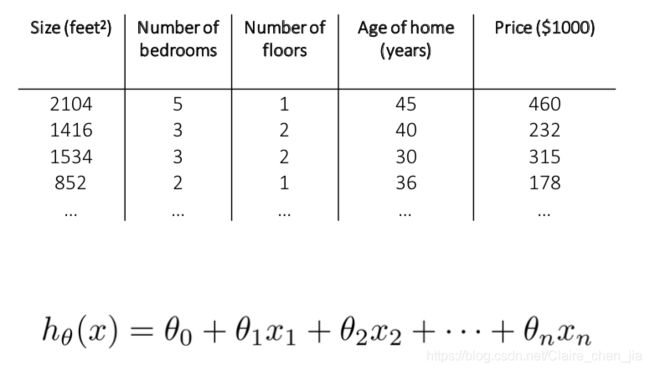
也就是说,当Y值的影响因素不是唯一时,就采用多元线性回归模型


下面简单用个例子,分别用API实现,和用代码算法实现 介绍一哈
- 用API实现
from sklearn import linear_model
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 读取数据
data = genfromtxt('Delivery.csv', delimiter=',')
# 数据切分
x_data = data[:,:-1]
y_data = data[:, -1]
print(x_data, y_data)
# 创建模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
print(model.coef_)
x_test = [[90, 2]]
predict = model.predict(x_test)
print(predict)
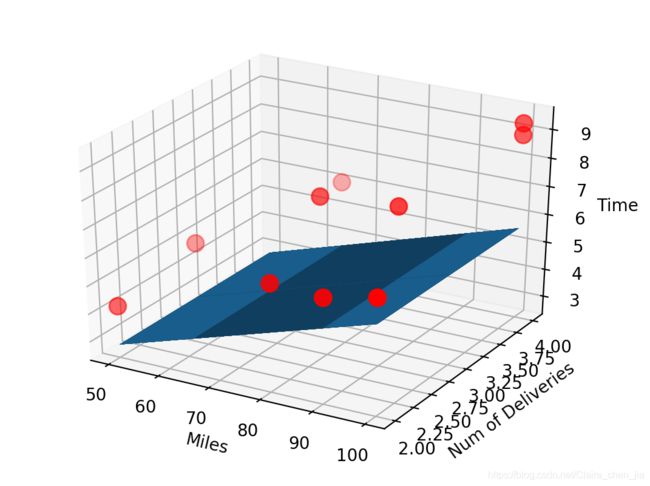
ax = plt.figure().add_subplot(111, projection='3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c='r', marker='o', s=100) # 点为红色三角形
x0 = x_data[:, 0]
x1 = x_data[:, 1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + x0 * model.coef_[0] + x1 * model.coef_[1]
# 画3D图
ax.plot_surface(x0, x1, z)
# 设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')
# 显示图像
plt.show()
- 用代码算法实现
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 读入数据
data = genfromtxt(r"线性回归2\Delivery.csv", delimiter=',')
# 切分数据
x_data = data[:, :-1]
y_data = data[:, -1]
print(x_data)
# 学习率,迭代次数,初始theta值
lr = 0.0001
epochs = 50
theta0 = 0
theta1 = 0
theta2 = 0
# 定义损失函数
def error_caculate(theta0,theta1,theata2,x_data,y_data):
error = 0
for i in range(len(x_data)):
predict_y = theta0 + theta1 * x_data[i,0] + theta2 * x_data[i,1]
error += (predict_y - y_data)**2
return error / float(len(x_data))
# 定义梯度下降迭代过程
def gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs):
# 计算总数据量
m = len(x_data)
# 循环epochs次
for i in range(0,epochs):
theta0_grad = 0
theta1_grad = 0
theta2_grad = 0
for j in range(0,len(x_data)):
theta0_grad += (1 / m) * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
theta1_grad += (1 / m) * x_data[j, 0] * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
theta2_grad += (1 / m) * x_data[j, 1] * ((theta1 * x_data[j, 0] + theta2 * x_data[j, 1] + theta0) - y_data[j])
# 更新b和k
theta0 = theta0 - (lr * theta0_grad)
theta1 = theta1 - (lr * theta1_grad)
theta2 = theta2 - (lr * theta2_grad)
# 每迭代5次,输出一次图像
if i % 5 == 0:
print("epochs:", i)
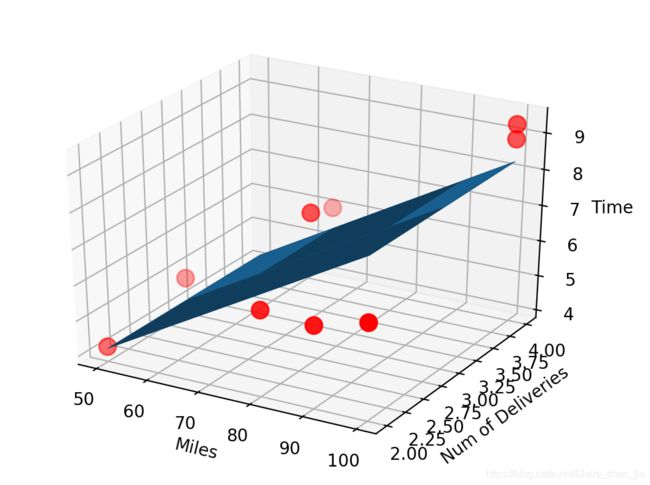
ax = plt.figure().add_subplot(111, projection='3d')
ax.scatter(x_data[:, 0], x_data[:, 1], y_data, c='r', marker='o', s=100) # 点为红色三角形
x0 = x_data[:, 0]
x1 = x_data[:, 1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = theta0 + x0 * theta1 + x1 *theta2
# 画3D图
ax.plot_surface(x0, x1, z)
# 设置坐标轴
ax.set_xlabel('Miles')
ax.set_ylabel('Num of Deliveries')
ax.set_zlabel('Time')
# 显示图像
plt.show()
return theta0, theta1, theta2
print("Starting theta0 = {0}, theta1 = {1}, theta2 = {2}, error = {3}".format(theta0, theta1, theta2, error_caculate(theta0, theta1, theta2, x_data, y_data)))
print("Running...")
theta0, theta1, theta2 = gradient_descent_runner(x_data, y_data, theta0, theta1, theta2, lr, epochs)
print("After {0} iterations theta0 = {1}, theta1 = {2}, theta2 = {3}, error = {4}".format(epochs, theta0, theta1, theta2, error_caculate(theta0, theta1, theta2, x_data, y_data)))