vivo笔试题(含答案)
总结不易,如果对你有帮助,请点赞关注支持一下
微信搜索程序dunk,关注公众号,定期分享Java笔试、面试题
目录
- 编译依赖问题(90% -> AC)
-
- 自己的做法
- 分析一下错误
- 改进(AC)
- 回文字符串(AC)
- 游戏地图路径(AC)
-
- 记忆化搜索
- 2021/6/6更新
- 手机屏幕解锁模式(60% -> AC)
-
- 60%
- AC
- 数位之积(AC)
-
- 递归 + 记忆
- vivo智能手机产能(AC)
-
- Easy
编译依赖问题(90% -> AC)
一个完整的软件项目往往会包含很多由代码和文档组成的源文件。编译器在编译整个项目的时候,可能需要按照依赖关系来依次编译每个源文件。比如,A.cpp 依赖 B.cpp,那么在编译的时候,编译器需要先编译 B.cpp,才能再编译 A.cpp。 假设现有 0,1,2,3 四个文件,0号文件依赖1号文件,1号文件依赖2号文件,3号文件依赖1号文件,则源文件的编译顺序为 2,1,0,3 或 2,1,3,0。现给出文件依赖关系,如 1,2,-1,1,表示0号文件依赖1号文件,1号文件依赖2号文件,2号文件没有依赖,3号文件依赖1号文件。请补充完整程序,返回正确的编译顺序。注意如有同时可以编译多个文件的情况,按数字升序返回一种情况即可,比如前述案例输出为:2,1,0,3
输入例子1:
"1,2,-1,1"
输出例子1:
"2,1,0,3"
自己的做法
比较迷,看到这道题第一反应,这不是并查集吗,奥不对,并查集是只能找到最顶级的依赖,这个题明显不是这个意思,然后自己做了一个多叉树吧,应该叫字典树吧,每个节点保存当前信息和所有依赖它的节点信息,用一个list集合存放所有的顶级节点,最终dfs输出就行,只通过了90%
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 编译顺序
* @param input string字符串
* @return string字符串
*/
StringBuilder builder = new StringBuilder();
public String compileSeq (String input) {
// write code here
Map<Integer, DependTree> map = new HashMap();
List<Integer> res = new ArrayList<>();
String[] depends = input.split(",");
for (int i = 0; i < depends.length; i++) {
int child = i;
int parent = Integer.parseInt(depends[i]);
if (parent == -1) {
res.add(child);
if (!map.containsKey(child))
map.put(child, new DependTree(child));
continue;
}
if (map.containsKey(parent)) {
DependTree PT = map.get(parent);
DependTree CP = null;
if (map.containsKey(child)) {
CP = map.get(child);
} else {
CP = new DependTree(child);
map.put(child, CP);
}
PT.child.add(CP);
} else {
DependTree PT = new DependTree(parent);
map.put(parent, PT);
DependTree CP = null;
if (map.containsKey(child)) {
CP = map.get(child);
} else {
CP = new DependTree(child);
map.put(child, CP);
}
PT.child.add(CP);
}
}
for (int i = 0; i < res.size(); i++) {
dfs(map.get(res.get(i)));
}
return builder.toString().substring(0, builder.length() - 1);
}
private void dfs(DependTree dependTree) {
builder.append(dependTree.val + ",");
for(DependTree sub : dependTree.child) {
dfs(sub);
}
}
}
class DependTree {
public int val;
public List<DependTree> child = new ArrayList<>();
public DependTree(int val) {
this.val = val;
}
}
分析一下错误
您的代码已保存
答案错误:您提交的程序没有通过所有的测试用例
case通过率为90.00%
用例:
“8,2,7,4,6,-1,5,5,6”
对应输出应该为:
“5,6,4,3,7,2,1,8,0”
你的输出为:
“5,6,4,3,8,0,7,2,1”
画一下依赖树
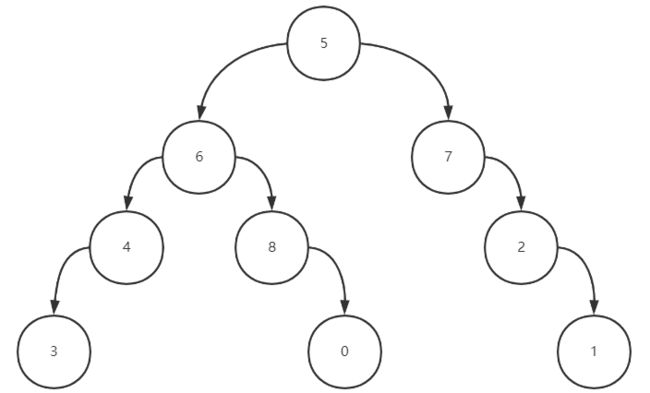
发现问题,没有满足按数字升序返回一种情况即可
改进(AC)
使用优先队列
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 编译顺序
* @param input string字符串
* @return string字符串
*/
StringBuilder builder = new StringBuilder();
public String compileSeq (String input) {
// write code here
Map<Integer, DependTree> map = new HashMap();
List<Integer> res = new ArrayList<>();
String[] depends = input.split(",");
for (int i = 0; i < depends.length; i++) {
int child = i;
int parent = Integer.parseInt(depends[i]);
if (parent == -1) {
res.add(child);
if (!map.containsKey(child))
map.put(child, new DependTree(child));
continue;
}
if (map.containsKey(parent)) {
DependTree PT = map.get(parent);
DependTree CP = null;
if (map.containsKey(child)) {
CP = map.get(child);
} else {
CP = new DependTree(child);
map.put(child, CP);
}
PT.child.add(CP);
} else {
DependTree PT = new DependTree(parent);
map.put(parent, PT);
DependTree CP = null;
if (map.containsKey(child)) {
CP = map.get(child);
} else {
CP = new DependTree(child);
map.put(child, CP);
}
PT.child.add(CP);
}
}
PriorityQueue<DependTree> queue = new PriorityQueue<DependTree>(Comparator.comparingInt(o -> o.val));
res.sort(Integer::compareTo);
for (int i = 0; i < res.size(); i++) {
queue.offer(map.get(res.get(i)));
while (!queue.isEmpty()) {
DependTree cur = queue.poll();
for(DependTree sub : cur.child) {
queue.offer(sub);
}
builder.append(cur.val + ",");
}
}
return builder.toString().substring(0, builder.length() - 1);
}
}
class DependTree {
public int val;
public List<DependTree> child = new ArrayList<>();
public DependTree(int val) {
this.val = val;
}
}
回文字符串(AC)
回文字符串就是正读和反读都一样的字符串,如“viv”、“nexen”、“12321”、“qqq”、“翻身把身翻” 等。
给定一个非空字符串 str,在最多可以删除一个字符的情况下请编程判定其能否成为回文字符串;如果可以则输出首次删除一个字符所能得到的回文字符串,如果不行则输出字符串 “false” 。
输入描述:
一个非空字符串
输出描述:
一个回文字符串,或者 "false" 字符串(如果无法构造出回文字符串的话)
输入z子1:
abda
输出例子1:
ada
例子说明1:
删除字符串"abda"中的一个字符 ‘b’ 后,得到 "ada"是一个回文字符串;删除一个字符 ‘d’ 后,得到 "aba"也是一个回文字符串;所以最终输出为 "ada"。
有点懵逼,明明是最多删除一个字符的情况,但是不删除的情况是错的
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String input = in.next();
int index = 0;
for (int i = 0; i < input.length(); i++) {
StringBuilder builder = new StringBuilder(input);
builder.delete(i, i + 1);
if (isPalindrome(builder.toString())) {
System.out.println(builder.toString());
return;
}
}
System.out.println(false);
}
private static boolean isPalindrome(String input) {
int l = 0;
int r = input.length() - 1;
while (l <= r) {
if (input.charAt(l) != input.charAt(r)) return false;
l++;
r--;
}
return true;
}
}
游戏地图路径(AC)
vivo游戏中心的运营小伙伴最近接到一款新游戏的上架申请,为了保障用户体验,运营同学将按运营流程和规范对其做出分析评估。经过初步了解后分析得知,该游戏的地图可以用一个大小为 n*n 的矩阵表示,每个元素可以视为一个格子,根据游戏剧情设定其中某些格子是不可达的(比如建筑、高山、河流或者其它障碍物等),现在请你设计一种算法寻找从起点出发到达终点的最优抵达路径,以协助运营小伙伴评估该游戏的可玩性和上手难度。
输入描述:
第一行表示矩阵大小 n,5 输出描述:
输出最优路径的长度;若无法到达,则输出-1
输入例子1:
15
0 7 7 7
*5#++B+B+++++$3
55#+++++++###$$
###$++++++#+*#+
++$@$+++$$$3+#+
+++$$+++$+4###+
A++++###$@+$++A
+++++#++$#$$+++
A++++#+5+#+++++
+++$$#$++#++++A
+++$+@$###+++++
+###4+$+++$$+++
+#+3$$$+++$##++
+#*+#++++++#$$+
$####+++++++$##
3$+++B++B++++#5
输出例子1:
13
记忆化搜索
import java.util.*;
public class Main {
static int N, endX, endY;
static int[][] dirs = {
{
-1, 0}, {
1, 0}, {
0, -1}, {
0, 1}};
static int[][] map;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
N = in.nextInt();
int startY = in.nextInt();
int startX = in.nextInt();
endY = in.nextInt();
endX = in.nextInt();
int[][] grid = new int[N][N];
for (int i = 0; i < N ; i++) {
String line = in.next();
for (int j = 0; j < N; j++) {
if (line.charAt(j) == '#' || line.charAt(j) == '@') {
grid[i][j] = -1;
}
}
}
map = new int[N][N];
/*for (int[] res : map) {
System.out.println(Arrays.toString(res));
}
System.out.println();*/
for (int i = 0; i < map.length; i++)
Arrays.fill(map[i], Integer.MAX_VALUE);
dfs(startX, startY, 0, grid);
if (map[endX][endY] == Integer.MAX_VALUE) {
System.out.println(-1);
} else {
System.out.println(map[endX][endY]);
}
}
private static void dfs(int startX, int startY, int count, int[][] grid) {
if (startX < 0 || startX >= N
|| startY < 0 || startY >= N
|| grid[startX][startY] == -1
|| count >= map[startX][startY])
return;
map[startX][startY] = count;
for (int[] dir : dirs) {
int curX = startX + dir[0];
int curY = startY + dir[1];
dfs(curX, curY, count + 1, grid);
}
}
}
2021/6/6更新
手机屏幕解锁模式(60% -> AC)
现有一个 3x3 规格的 Android 智能手机锁屏程序和两个正整数 m 和 n ,请计算出使用最少m 个键和最多 n个键可以解锁该屏幕的所有有效模式总数。
其中有效模式是指:
1、每个模式必须连接至少m个键和最多n个键;
2、所有的键都必须是不同的;
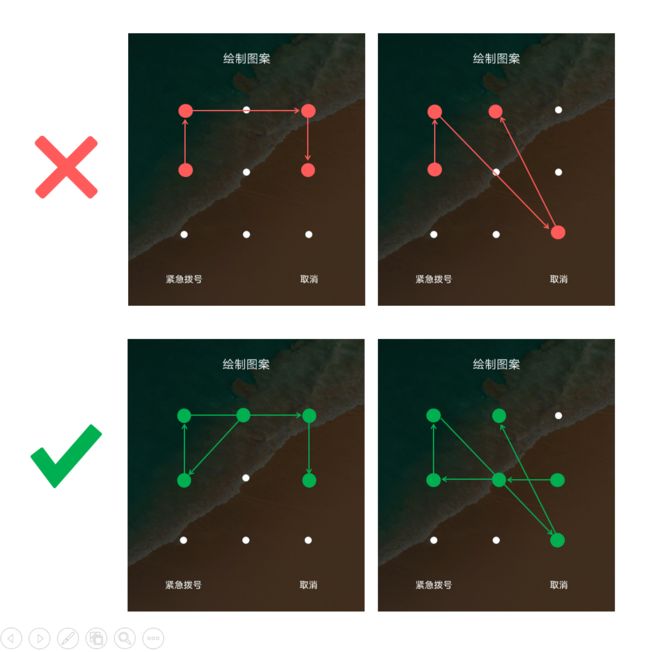
3、如果在模式中连接两个连续键的行通过任何其他键,则其他键必须在模式中选择,不允许跳过非选择键(如图);
4、顺序相关,单键有效(这里可能跟部分手机不同)。
输入:m,n
代表允许解锁的最少m个键和最多n个键
输出:满足m和n个键数的所有有效模式的总数
输入例子1:
1,2
输出例子1:
65
例子说明1:
输入m=1,n=2,表示最少1个键,最多2个键,符合要求的键数是1个键和2个键,其中1个键的有效模式有9种,两个键的有效模式有56种,所以最终有效模式总数是9+56=65种,最终输出65。
60%
思路:没得说,递归吧
import java.util.*;
public class Solution {
/**
* 实现方案
* @param m int整型 最少m个键
* @param n int整型 最多n个键
* @return int整型
*/
int min, max;
int sum;
public int solution (int m, int n) {
// write code here
if(m > n) return 0;
this.min = m;
this.max = n;
sum = 0;
boolean[][] isVisit = new boolean[3][3];
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
isVisit[i][j] = true;
dfs(i, j, isVisit, 1);
isVisit[i][j] = false;
}
}
return sum;
}
private void dfs(int x, int y, boolean[][] isVisit, int keys) {
if (keys >= min && keys <= max) {
sum++;
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
int dx = Math.abs(i - x);
int dy = Math.abs(j - y);
if (isVisit[i][j]) continue;
if (dx % 2 == 0 && dy % 2 == 0 && !isVisit[dx / 2][dy / 2]) {
continue;
}
isVisit[i][j] = true;
dfs(i, j, isVisit, keys + 1);
isVisit[i][j] = false;
}
}
}
}
AC
import java.util.*;
public class Solution {
/**
* 实现方案
* @param m int整型 最少m个键
* @param n int整型 最多n个键
* @return int整型
*/
public static int solution (int m, int n) {
// 递归实现
int count = 0;
n = n>9 ? 9 : n;
for(int i=m;i<=n;i++) {
boolean[][] flags = new boolean[3][3];
for(int j=0;j<3;j++) {
for(int t=0;t<3;t++) {
count += findNext(flags, j, t, 0, i);
}
}
}
return count;
}
public static int findNext(boolean[][] flags,int curRow, int curCol, int steps, int n) {
int count = 0;
steps ++;
flags[curRow][curCol] = true;
// 步数走完返回
if(steps == n)
return 1;
// 如果可以走,那么返回 1
for(int i=0;i<3;i++) {
for(int j=0;j<3;j++) {
if(flags[i][j] == false && canStep(flags, curRow, curCol, i, j)) {
count += findNext(flags, i, j, steps, n);
// 恢复状态
flags[i][j] = false;
}
}
}
flags[curRow][curCol] = false;
return count;
}
public static boolean canStep(boolean[][] flags, int curRow, int curCol, int targetRow, int targetCol) {
// 在同一行
if(curRow == targetRow) {
int low = curCol < targetCol?curCol:targetCol;
if(Math.abs(curCol - targetCol) >1 && flags[curRow][low+1] == false)
return false;
}
// 在同一列
if(curCol == targetCol) {
int low = curRow < targetRow?curRow:targetRow;
if(Math.abs(curRow - targetRow) >1 && flags[low+1][curCol] == false)
return false;
}
// 斜对角
if(Math.abs(curRow-targetRow)==2 && Math.abs(curCol-targetCol)==2 && flags[1][1] == false)
return false;
return true;
}
}
数位之积(AC)
现给定任意正整数 n,请寻找并输出最小的正整数 m(m>9),使得 m 的各位(个位、十位、百位 … …)之乘积等于n,若不存在则输出 -1。
输入例子1:
36
输出例子1:
49
输入例子2:
100
输出例子2:
455
递归 + 记忆
思路:让n除以从9 - 2的,如果整除:n变为n / i递归,并且将i放入list集合中
import java.util.*;
public class Solution {
/**
* 输入一个整形数值,返回一个整形值
* @param n int整型 n>9
* @return int整型
*/
List<Integer> res = new ArrayList<>();
public int solution (int n) {
dfs(n, new ArrayList<>());
int num = 0;
for (int i = res.size() - 1; i >= 0; i--) {
num = num * 10 + res.get(i);
}
return num == 0 ? -1 : num;
}
private void dfs(int n, ArrayList<Integer> list) {
if (res.size() != 0) return;
if (n == 1) {
res = new ArrayList<>(list);
return;
}
ArrayList<Integer> sub = new ArrayList<>(list);
for(int i = 9; i >= 2; i--) {
if (n % i == 0) {
sub.add(i);
dfs(n / i, sub);
}
}
}
}
vivo智能手机产能(AC)
在vivo产线上,每位职工随着对手机加工流程认识的熟悉和经验的增加,日产量也会不断攀升。
假设第一天量产1台,接下来2天(即第二、三天)每天量产2件,接下来3天(即第四、五、六天)每天量产3件 … …
以此类推,请编程计算出第n天总共可以量产的手机数量。
输入例子1:
11
输出例子1:
35
例子说明1:
第11天工人总共可以量产的手机数量
Easy
import java.util.*;
public class Solution {
/**
*
* @param n int整型 第n天
* @return int整型
*/
public int solution (int n) {
// write code here
int sum = 0;
int index = 1;
while(n > 0) {
if(n > index) {
n -= index;
sum += index * index;
} else {
sum += n * index;
n = 0;
}
index++;
}
return sum;
}
}
后面会不断更新新的试题…