红黑树进阶—左倾红黑树（LLBR）介绍

红黑树已经有很长的历史，在许多现代编程语言的符号表中都有使用，但是其缺点也很明显，其代码实现过于繁杂。因此出现的红黑树的修改版——左倾红黑树

左倾红黑树的代码实现相比于典型的红黑树来说要简单不少，但是国内论坛好像并没有一个对于左倾红黑树相对系统的介绍，因此我找到了左倾红黑树的论文并将其整理翻译，以供学习

由于过于繁杂，因此翻译的时候未对性能分析部分进行翻译，在这里提供原文地址

在阅读本文前读者需要详细的了解二叉搜索树（BST）、红黑树、2-3树及2-3-4树

由于能力有限，因此翻译的时候难免有不准确的地方，这个翻译仅供学习参考

论文地址：http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.139.282

左倾红黑树
罗伯特塞奇威克
计算机科学系
普林斯顿大学
普林斯顿，新泽西州08544

简介

在用于实现平衡搜索的红黑树模型现在遍布我们的计算基础设施，在许多标准教科书中都有对红黑树的描述，是C++，Java，Python，BSD Unix等许多现代系统中符号表实现的基础数据结构。但是，其中许多实现牺牲了一些原始设计目标，因此设计一种新的模式是有价值的。

在这篇论文中，描述了一种新的红黑树变体，它满足了许多原始设计目标，并且导致插入/删除的代码简单的多，仅需要常用实现代码的四分之一。

所有红黑树都是基于2-3树或2-3-4树的变种，使用红色链接绑定到三节点或四节点。新代码基于三个概念的组合：

1：使用递归实现

2：要求所有三节点向左倾斜

3：在树的上面执行旋转（在执行递归之后）

这些想法不仅能生成简单的代码，而且还能统一算法：例如在2-3树的左倾版本和2-3-4树中的自顶向下的版本在一行代码的位置不同

具体来说，在由一个N个键构成的左倾红黑2-3树种，一个搜索操作需要检查lgN - 0.5个节点，树的平均高度约为2ln n

在LLBR（左倾红黑树）中由许多吸引人的特性：

1：实验研究未能将这些算法与最优算法区分开

2：它可以通过向标准BST（二叉搜索树）算法添加几行代码来实现。

3：与散列表不同，他们支持有序操作，如：SELECT，RANK，RANGE搜索

因此LLRB树对于各种符号表应用程序都很有用，并且是未来软件库中作为符号表基础的主要候选对象

介绍

我们在本文中关注的是包含通用键和关联值得符号表中提供以下操作的有效实现的目标：

1：搜索/获取与给定键关联的值

2：将键值对插入符号表中

3：使用符号表中给定的键删除键值对

4：当插入操作涉及表中已有的键时，我们将该键与指定的新值关联，因此表中没有重复的键

我们进一步假设键是可比较的：我们有一个比较操作可以确定一个给定的键是否小于，等于，或大于另一个给定的键，这样我们就可以保留实现有序关联数组的能力，我们可以支持搜索、范围搜索和类似的操作。

红黑树最重要的特征之一是他们不会增加搜索的开销，这是最常用的操作。因此，红黑树是C++，Java，Python，BSD Unix和许多其他系统中符号表实现的基础数据结构，为什么要重新审视这样一个成功的数据结构？在实现红黑树的时候，实际的代码很难维护并在新系统中重用，因为它很长，在典型的实现代码有100 - 200行代码，教科书中很少有完整实现。在本文中，我们提出了一种可以大大减少所需代码量的方法。为了证明这一点，我们提出一个完整的Java实现，包括三个简短使用的方法，为标准BST代码添加3行代码以进行插入，使用5行代码删除最大值，以及额外30行删除代码

旋转和颜色翻转

观察红黑树算法的一种方法是在插入和删除操作下维护以下不变的属性：

1：从跟到低的路径不包含两个连续的红色链接

2：每个路径上黑色链接的数量是相同的

这些不变量限制了有N个节点的红黑树每条路径长度不会2lgn，这种最糟糕的情况发生在一个节点都是黑色的树中

平衡树算法用于在插入和删除下保持平衡的基本操作称为旋转。

在红黑树的前提下，这些操作很容易理解为将红色链接向左倾斜的3节点转换为向右倾斜和反向倾斜的3节点所需的转换

旋转操作显然保留了上述两个不变量，在红黑树中，我们还使用一种称为颜色翻转（color flip）的简单操作。就2-3-4树而言，颜色翻转是必不可少的操作：它对应于分割4节点并将中间节点传递给父节点，颜色翻转显然不会改变从跟到底的任何路径上黑色链接的数量，但是它可能在树中引入两

个连续的红色链接，必须进行更正

红黑树算法在是否以及何时进行旋转和颜色翻转方面存在差异，以便维护上面的不变量

左旋（Left rotate）

右旋（Right rotate）

颜色翻转

该串代码将节点h及h的两个孩子颜色翻转，变为与之前相反的颜色。具体的Node类型会在后面阐述

左倾红黑树

代码的起点是标准BST的Java实现，如下面的代码所示。在下面的代码中使用泛型以一种类型安全的方式实现，如果不使用泛型则代码是标准的，可以轻松的翻译成其他语言或应用于不需要泛型类型的特定应用程序。

在目前的上下文中，实现的一个重要特性是insert()的实现是递归的：每个递归都以一个链接（link）作为参数并返回一个链接，该链接用于重置从该链接获取的字段（这么说很抽象，原文大概原意就是每次递归获得一个新的节点，用这个新的节点再次进行递归）。对于标准的BST，除了树的底部，参数和返回值是相同的。这里的代码（insert()）用于插入新节点。对于红黑树，这个递归有助于简化代码

除此之外，对于search()操作也可以使用递归实现。但是这里并不会使用递归实现，因为这个操作属于典型的程序内部循环，实现红黑树算法的基础实在这段代码中添加旋转和颜色翻转操作。以便维护树中的平衡不变量

在本文的代码中，我们展示了可以通过以下方式来大大减少需要考虑的情况：

1：要求3节点总是向左倾斜（并且4节点是平衡的）

2：在递归调用之后，在树的路径上进行旋转

向左倾斜的要求给出了红黑树和2-3-4树之间的1-1对应关系，并减少了需要考虑的情况数量。

循环向上旋转策略通过一种自然方式组合各种情况简化了代码（以及我们对它的理解），这两种方法并不是什么新方法，但是二者结合在一起在减少代码数量方面却出奇的有效。

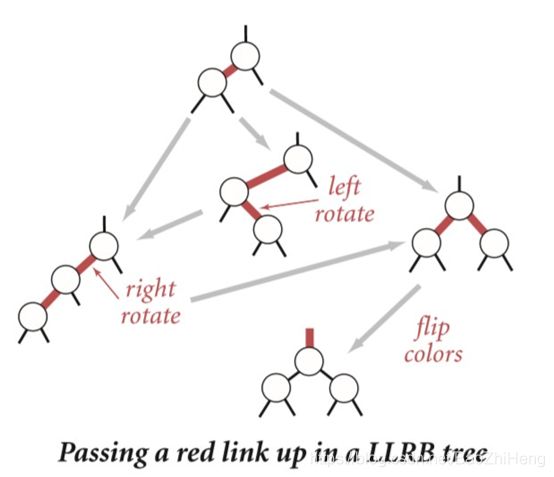
自顶向下的2-3-4树插入一个新节点，我们翻转颜色以分割在树下的路径上遇到的任何4节点并并进行旋转以平衡4节点（消除在树上出现的连续的红色链接）。这种方法是很自然的，因为分裂4节点以确保搜索不会在4节点上终止，意味着可以通过附加红色链接添加新节点，并平衡4节点数量，平衡4节点的三种方式如下面的图片所示。如果传递的红色连接恰好在3节点中向右倾斜，我们在遇到它时会纠正这种情况

2-3树值得注意的时，在上面描述的自上而下的2-3-4树实现中，将颜色翻转移动到最后，产生了2-3树的实现，我们将通过颜色翻转，向树传递红色连接，以及在树中移动时以完全相同的方式处理这样做的效果

在左倾红黑树中传递一个红色节点

public class LLRB<Key extends Comparable<Key>, Value> {
        

	private static final boolean RED   = true;  
	private static final boolean BLACK = false;
	private Node root;
	private class Node{
          
		private Key key;     
		private Value val;     
		private Node left, right;      
		private boolean color;      //用一位字段表示颜色
		Node(Key key, Value val){
              
			this.key = key;  
			this.val = val;        
			this.color = RED;     //新节点总是红色

		}   
	}

	public Value search(Key key){
           

		Node x = root;     
		while (x != null){
             
			int cmp = key.compareTo(x.key);         
			if (cmp == 0) return x.val;         
			else if (cmp < 0) x = x.left;         
			else if (cmp > 0) x = x.right;      
		}      
		return null;   
	}
	
	public void insert(Key key, Value value){
            
		root = insert(root, key, value);       
		root.color = BLACK;  
	}   

	private Node insert(Node h, Key key, Value value){
            
		if (h == null) return new Node(key, value);
		if (isRed(h.left) && isRed(h.right)) colorFlip(h);  //这一行开始	
		int cmp = key.compareTo(h.key);  
		if (cmp == 0) h.val = value;       
		else if (cmp < 0) h.left =  insert(h.left, key, value);      
		else h.right = insert(h.right, key, value);
		if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);       
		if (isRed(h.left) && isRed(h.left.left)) h =rotateRight(h);  //到这里运行结束时，得到2-3树
		return h;   
	} 
} 

删除

在许多符号表实现中，删除操作的高效实现是一个挑战，红黑树也不例外，工业级的实现可以运行超过100行代码。教科书一般以详细的案例研究的方式描述操作，避免完整的实现

下面的代码是LLRB 2-3树的delete()完整实现，它是基于反向自顶向下的方法用于插入2-3-4树：

我们进行旋转和颜色翻转向下搜索路径，以确保搜索不会在2节点上结束，这样我们就可以删除底部节点，我们使用fixUp()方法共享insert()代码中递归调用后的颜色翻转和旋转代码，通过fixUp()，我们可以在搜索路径上留下右倾斜的红色链接和不平衡的四个节点，确保这些问题在沿树上升的时候会被修复（这种方法也适用于2-3-4树，但如果搜索路径上的右节点是4节点，则需要额外的旋转。）

作为热身，考虑删除最小操作，目标是删除左边脊柱（left spine）的底部节点，同时保持平衡。为此，我们维护当前节点或者其左孩子的红色不变式，我们可以通过向左移动（move to the left）来实现，除非当前节点是红色的，其左孩子和左孙子（left grandchild，还是叫左孩子的左孩子合适一些？）都是黑的。在这种情况下我们可以做一个颜色翻转，它可以恢复不变量，但可能会在右边引入连续的红色节点，在这种情况下，我们可以通过两个旋转和一个颜色翻转来修正条件，这些操作是在下面的moveRedLeft()方法中实现的。

使用moveRedLeft()使得deleteMin()的递归实现非常简单，对于一般的删除，我们还需要moveRedRight()，它与moveRedLeft()类似，但是更简单，并且我们需要在搜索路径上将左边的红色链接旋转到右侧以保持不变量。如果要删除的节点是内部节点，我们将其键和值字段替换为其右子树中的最小节点字段，然后删除右子树中最小值字段（或者我们可以重新安排指针来使用节点而不是复制字段）。

在下面给出了本文所讨论的delete()的完整实现，它使用的代码量仅仅是红黑树典型实现的三分之一到四分之一，使用LLRB树，我们可以设计出简洁的代码，而且具有对数级别的性能保证，还不会使用额外的空间

删除左倾红黑 2-3树的最小值代码（Delete-the-minimum code for LLRB 2-3 trees）

public void deleteMin() {
        
	root = deleteMin(root);  
	root.color = BLACK;
 }

private Node deleteMin(Node h) {
        
	if (h.left == null) return null;
	if (!isRed(h.left) && !isRed(h.left.left))h = moveRedLeft(h);
	h.left = deleteMin(h.left);
	return fixUp(h); 
} 

从左倾红黑 2-3树中删除节点（Delete code for LLRB 2-3 trees）

 private Node moveRedLeft(Node h){
     
	colorFlip(h);      
    if(isRed(h.right.left)){
      
   	 h.right =rotateRight(h.right);  
   	 h =rotateLeft(h);        
   	 colorFlip(h);     
    }     
return h;  
}

private Node moveRedRight(Node h){
       
   colorFlip(h);       
   if (isRed(h.left.left)){
        
   	h = rotateRight(h);   
   	colorFlip(h);     
   }      	
    return h;  
}

 
public void delete(Key key){
      
   root = delete(root, key); 
   root.color = BLACK;   
 }

private Node delete(Node h, Key key){
      
   if (key.compareTo(h.key) < 0){
                  
   	if (!isRed(h.left) && !isRed(h.left.left)) h = moveRedLeft(h);              
   	h.left =  delete(h.left, key);         
   } else {
          
   	if (isRed(h.left)) h = rotateRight(h); 
   	if (key.compareTo(h.key) == 0 && (h.right == null)) return null;              
   	if (!isRed(h.right) && !isRed(h.right.left)) h = moveRedRight(h);           

   if (key.compareTo(h.key) == 0){
           
   	h.val = get(h.right, min(h.right).key);            
   	h.key = min(h.right).key;                   
   	h.right = deleteMin(h.right);             
   }else h.right = delete(h.right, key);  
}
return fixUp(h); 
}

图示：