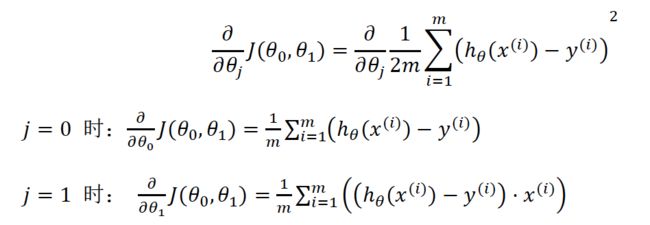代码来自黄海广博士的github,按自己的理解增加了详细的注释。感谢黄博士的开源。
https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
一、题目要求
单变量和多变量线性回归:给出一组数据数据,用线性回归方法拟合函数。预测开一家餐馆的盈利,预测房价。涉及的内容不少,连学python到全部理解用了两天时间。
内容:
- 单变量-餐馆盈利预测
- 多变量-房价预测
- 现有库实现梯度下降
- 正规方程硬解拟合参数
二、单变量拟合的代码实现与说明,完整代码参考原作者的github
1. 数据预处理
// 导入依赖库,常用的数据处理和绘图工具
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
// 读取样本数据
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
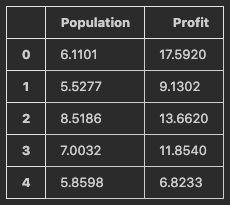
// 列举前面几组数据展示
data.head()
// 描述样本数据的基本特征
data.describe()
data(DataFrame类实例)
用绘图的方式看看数据的分布
// scatter表示离散
// data.plot底层用的也是matplotlib的方法绘制
// ?没找到这个方法如何改变背景,默认的背景是透明的
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))
plt.show()
2. 定义损失函数
现在让我们使用梯度下降来实现线性回归,以最小化成本函数。 以下代码示例中实现的方程在“练习”文件夹中的“ex1.pdf”中有详细说明。
首先,我们将创建一个以参数θ为特征函数的代价函数
其中
代码实现:
def computeCost(X, y, theta):
X * theta.T
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
让我们在训练集中添加一列,以便我们可以使用向量化的解决方案来计算代价和梯度。因为有项,所以x的第一列加上“1”,相当于给一个基准起始值,一般称为“截距”
data.insert(0, 'Ones', 1) // 在第0列的位置添加1,列的名称为“Ones”
data.describe() // 更新好,打印下数据特征
变量初始化
cols = data.shape[1] // data的大小,可以理解为size、length等,矩阵为:行 * 列
// iloc按index取列, loc按名称曲烈
// python中" : "取全部值
// 0:cols-1 从0->clos-1选择列,即取所有x的列,最后一列是y的列
X = data.iloc[:,0:cols-1]#X是所有行,去掉最后一列
y = data.iloc[:,cols-1:cols]#X是所有行,最后一列
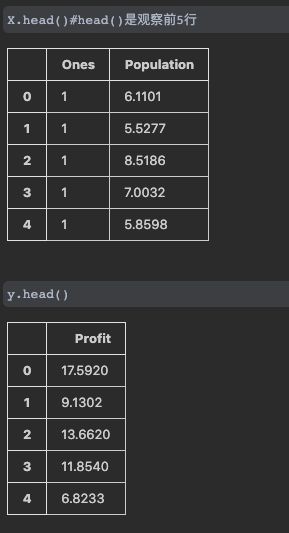
观察下 X (训练集) and y (目标变量)是否正确.
// 上面已经介绍过.head方法了
x.head()
y.head()
进入关键步骤了,代价函数是应该是numpy矩阵,所以我们需要转换X和Y,然后才能使用它们。 我们还需要初始化theta。
X = np.matrix(X.values)
Y = np.matrix(y.values)
// theta 是一个(1,2)矩阵,即1行2列,matrix([[0, 0]]),初始化为0
theta = np.matrix(np.array([0,0]))
// 看下 x y theta的维度
X.shape, Y.shape, theta.shape
// ((97, 2), (97, 1)), (1, 2)
// 计算代价函数
computeCost(X, y, theta)
// 这时theta为0,相当于计算的是y的方差,值为 32.072733877455676
定义梯度下降函数,batch gradient decent(批量梯度下降
按照偏导求出上面的表达式
注意,吴恩达的教程里,区分了j = 0和j = 1,是方便大家理解。在这里,对x增加了值为"1"的列,
按下面算式,值为1,不用区分
编程实现梯度下降,第一次看这个式子有点晕,对照上面的偏导求解的式子理解
注意也改成的方式来求
// X:观察的自变量
// y:观察的结果变量
// theta:参数 即theta0 和 theta1
// iters:迭代次数,后面定位为1000
def gradientDescent(X, y, theta, alpha, iters):
// 生成一个2 x 1的零矩阵
temp = np.matrix(np.zeros(theta.shape))
// .ravel() .flatten()作用相同,都是把数据降维度,平摊到一维数组,区别是flatten会重新生成一份数据,不影响原始引用的数据
// shape[1] 指列的数量,shape[0]指行的数量
parameters = int(theta.ravel().shape[1])
// 初始化一个零数组,长度为迭代次数,迭代一次,往里面填充一个对应的数据,后面绘制梯度下降效果图用得到
cost = np.zeros(iters)
for i in range(iters):
// 循环迭代,先计算损失函数的最里面的值
error = (X * theta.T) - y
for j in range(parameters):
// 再乘上对应的系数,注意这里是按照矩阵的方式一次性求出来
// 在这道题里,参数有两个 theta0和theta1,即parameters为0->1,迭代两次,这里没懂,回上面看下梯度下降的原理,每进行一次迭代,更新一次theta的值
term = np.multiply(error, X[:,j])
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
// 更新完theta, 一次小迭代技术,记录theta,下次迭代继续更新
theta = temp
// 迭代一次,计算一次损失函数,最后要绘制损失函数曲线图,用来分析收敛情况
cost[i] = computeCost(X, y, theta)
// 返回结果,注意,python里,可以返回多个值
return theta, cost
3. 运行梯度下降,求解拟合参数
// 步幅为0.01,后面课程中讲到,alpha可以调整为动态更新,先快后慢
alpha = 0.01
// 迭代1000次
iters = 1000
// 梯度结果为 g:theta,cost:损失值。得到g即得到了拟合的函数算子了
g, cost = gradientDescent(X, y, theta, alpha, iters)
// 基于g,计算损失函数
computeCost(X, y, g)
// 结果为 4.515955503078914
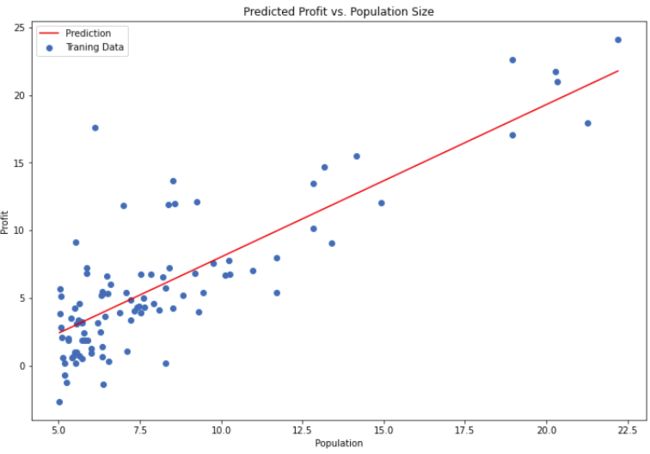
绘制线性模型以及数据,观察拟合情况
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x)
fig, ax = plt.subplots(figsize=(12,8))
fig.set_facecolor('white') //默认的背景是透明的,不好看,可以改成白底。
ax.plot(x, f, 'r', label='Prediction')
# ax.scatter(data.Population, data.Profit, label='Traning Data', s =60, c = 'b',
marker='+')
# 查下api “s”- 绘制点的大小,"c"-color颜色,'marker"-离散点的形状
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
观察损失函数瘦脸的情况,开始下降的很快,后面慢慢收敛,比较理想
二、多变量线性回归。逻辑和单变量类似,不再赘述。(增加了归一化处理)
练习1还包括一个房屋价格数据集,其中有2个变量(房子的大小,卧室的数量)和目标(房子的价格)。 我们使用我们已经应用的技术来分析数据集。
path = 'ex1data2.txt'
data2 = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
data2.head()
data2.describe()
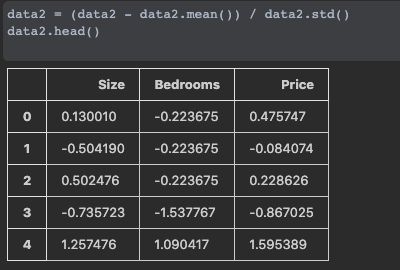
# 对于此任务,我们添加了另一个预处理步骤 - 特征归一化。 这个对于pandas来说很简单,注意特征归一化是机器学习数据预处理里非常重要的一环,直接影响模型训练的效率和结果,尤其是各个特征的量级差距很大。
data2 = (data2 - data2.mean()) / data2.std()
data2.head()
# 现在我们重复第1部分的预处理步骤,并对新数据集运行线性回归程序。
# add ones column
data2.insert(0, 'Ones', 1)
# set X (training data) and y (target variable)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]
# convert to matrices and initialize theta
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))
# perform linear regression on the data set
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
# get the cost (error) of the model
computeCost(X2, y2, g2)
# 计算结果为 0.1307033696077189,以我目前初学者的水平,并不能看出来这个值代表什么,是好还是坏呢?
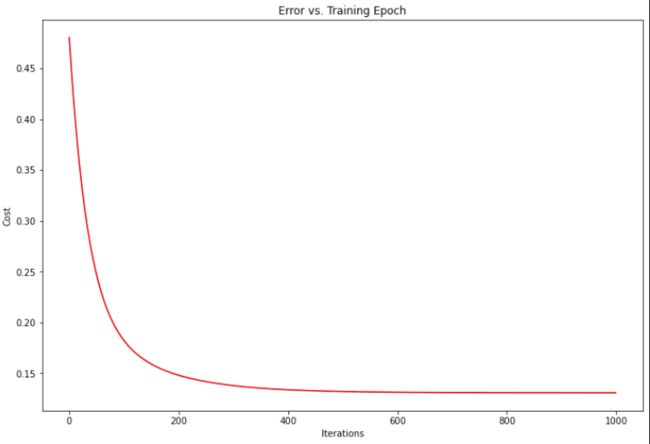
# 可以快速查看这一个的训练进程。
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
fig.set_facecolor('white');
plt.show()
数据形式:
归一化:
梯度下降曲线:
三、用现成的库来处理梯度下降,不用像上面自己搞半天
我们也可以使用scikit-learn的线性回归函数,而不是从头开始实现这些算法。 我们将scikit-learn的线性回归算法应用于第1部分的数据,并看看它的表现。
几行代码就可以实现:
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)
x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
fig.set_facecolor('white')
plt.show()
四、用解方程的方式求解参数,一般叫“正规方程-normal equation”
原理是用线性代数的最小二乘法来拟合,不记得最小二乘法,可以复习下。
#正规方程
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y#X.T@X等价于X.T.dot(X)
return theta
final_theta2=normalEqn(X, y)#感觉和批量梯度下降的theta的值有点差距
final_theta2
# 得到的结果为:matrix([[-3.89578088], [ 1.19303364]])
# 梯度下降得到的结果是matrix([[-3.24140214, 1.1272942 ]]),第一个参数即截距差距较大