JasonChiu17
JasonChiu17

支持向量机SVM

原理

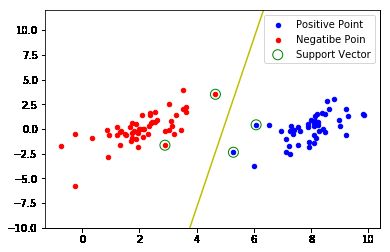
  • 寻找一个分割超平面来作为分类边界，找到离分割超平面最近的点，确保它们离分割超平面的距离尽可能远。
  • 支持向量就是离分割超平面最近的那些点

优点：

  • 泛化错误率低，计算开销不大，结果易解释。

缺点：

  • 对参数调节和核函数的选择敏感，原始分类器不加修改仅适用于处理二类问题。

适用数据类型：

  • 数值型和标称型数据。

简化版SMO算法

#加载数据
def loadData(path):
    #新建数据和标签列表
    dataList = [];labelList= []
    #获得文件指针
    fr = open(path)
    #一行一行读取
    for line in fr.readlines():
        #分割返回list
        lineList = line.strip().split()
        #取前1，2列作为训练数据
        dataList.append([float(lineList[0]),float(lineList[1])])
        #最后一列最为标签数据
        labelList.append(float(lineList[-1]))
    return dataList,labelList
dataList,labelList = loadData('../../Reference Code/Ch06/testSet.txt')

#随机选择alpha
import random
def selectJrand(i,m):     
    #这里可能随机取值会取到和i相等的值，为了j!=i，所以才先赋值j=1，再while循环
    j = i 
    while(j==i):
        j = int(random.uniform(0,m)) 
    return j

j = selectJrand(1,6)
# def selectJrand(m):
#     j = int(random.uniform(0,m))
#     return j
# j = selectJrand(6)
def clipAlpha(aj,H,L):
    if aj>H:
        aj = H
    if L>aj:
        aj = L
    return aj

import sys
print(sys.executable)

/home/ubuntu/anaconda3/bin/python

#简化版SMO
import numpy as np
def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
    '''
    参数：
        dataMatIn:输入数据
        classLabels：标签
        C：惩罚项
        toler：错误容忍度
        maxIter：最大迭代次数
    返回：
        b:偏置项
        alphas：拉格朗日乘子
    '''
    #数据和标签转化为ndarray
    #等价于dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).T
    dataArray = np.array(dataMatIn); labelArray = np.array(classLabels).reshape(-1,1)
    #初始化b，获得数据矩阵的行列
    b = 0; m,n = shape(dataArray)
    #初始化alphas全为0向量
    alphas = np.zeros((m,1))

    #初始化迭代次数
    Iter =0
    #当迭代次数小于最大迭代次数
    while (Iter toler) and (alphas[i] > 0)):
                #随机选择j，j!=i
                j = selectJrand(i,m)
                #计算g(xj)
                '''
                注意区别
                shape(dataArray[1,:]) #(2, )
                shape(dataArray[1,:].T)# (2, )
                shape(dataArray[1:2,:].T)(2, 1)
                '''
                fXj = float(np.dot((alphas*labelArray).T,np.dot(dataArray,dataArray[j:j+1,:].T))) + b
                #计算Ej
                Ej = fXj - float(labelArray[j])
                #赋值旧的alphai和alphaj
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                #若yi!=yj
                if (labelArray[i] != labelArray[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                #若yi=yj
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] - alphas[i])
                if L==H:print('L==H');continue
                #计算eta，参考李航PP127
                eta = 2.0*np.dot(dataArray[i],dataArray[j]) \
                - np.dot(dataArray[i],dataArray[i])\
                - np.dot(dataArray[j],dataArray[j])
                if eta >= 0:print('eta>=0');continue
                #跟新alphaj
                alphas[j] -= labelArray[j]*(Ei - Ej)/eta
                #若alphaj>H，则取H，若alphajalphas[i]):b = b1
                elif (0 < alphas[j]) and (C>alphas[j]): b = b2
                else: b = (b1+b2)/2.0
                #alpha对加一
                alphaPairsChanged += 1
                print("循环次数: {} alpha:{}, alpha对修改了 {} 次".format(Iter,i,alphaPairsChanged))
        if(alphaPairsChanged == 0): Iter += 1
        else: Iter = 0
        print("迭代次数: {}".format(Iter))
    return b,alphas

dataList,labelList = loadData('../../Reference Code/Ch06/testSet.txt')
b, alphas = smoSimple(dataList, labelList, 0.6, 0.001, 40)
print('b= {}'.format(b))
print('（支持向量对应的alpha>0）alpha>0\n{}'.format(alphas[alphas>0]))

循环次数: 0 alpha:0, alpha对修改了 1 次
循环次数: 0 alpha:2, alpha对修改了 2 次
L==H
j not moving enough
循环次数: 0 alpha:6, alpha对修改了 3 次
j not moving enough
j not moving enough
j not moving enough
循环次数: 0 alpha:22, alpha对修改了 4 次
j not moving enough
L==H
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
L==H
循环次数: 0 alpha:54, alpha对修改了 5 次
循环次数: 0 alpha:55, alpha对修改了 6 次
j not moving enough
L==H
j not moving enough
L==H
L==H
迭代次数: 0
j not moving enough
j not moving enough
L==H
L==H
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
L==H
L==H
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
循环次数: 0 alpha:97, alpha对修改了 1 次
迭代次数: 0
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
循环次数: 0 alpha:54, alpha对修改了 1 次
j not moving enough
j not moving enough
循环次数: 0 alpha:97, alpha对修改了 2 次
迭代次数: 0
j not moving enough
循环次数: 0 alpha:13, alpha对修改了 1 次

迭代次数: 25
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 26
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 27
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 28
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 29
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 30
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 31
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 32
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 33
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 34
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 35
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 36
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 37
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 38
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 39
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 40
b= [-4.48392829]
（支持向量对应的alpha>0）alpha>0
[0.02485639 0.33967041 0.26285541 0.1016714 ]

#打印支持向量
for i in range(len(dataList)):
    if alphas[i]>0.0:
        print(dataList[i],labelList[i])

[4.658191, 3.507396] -1
[2.893743, -1.643468] -1
[5.286862, -2.358286] 1
[6.080573, 0.418886] 1

import matplotlib.pyplot as plt
import numpy as np
def dataToShow(dataList,labelList,b,alphas):
    #array形式方便处理
    dataArray = np.array(dataList)
    alphasArray = np.array(alphas.tolist())
    #变成一列，-1表示自动计算多少行
    labelArray = np.array(labelList).reshape(-1,1)
    #正类负类分开画图,np.squeeze转化成一维的
    posData = dataArray[np.squeeze(labelArray>0.0)]    
    negData = dataArray[np.squeeze(labelArray<0.0)]
    svData = dataArray[np.squeeze(alphasArray>0.0)]
    plt.figure()
    plt.scatter(posData[:,0],posData[:,1],c='b',s=20)
    plt.scatter(negData[:,0],negData[:,1],c='r',s=20)
    plt.scatter(svData[:,0],svData[:,1],marker='o',c='',s=100,edgecolors='g')
    plt.legend(['Positive Point','Negatibe Poin','Support Vector'])
    #画分割超平面
    w = np.dot((alphasArray * labelArray).T, dataArray)
    x0 = np.array([2, 8])
    #分割线：w0*x0+w1*x1+b=0
    x1 = -(w[0, 0] * x0 + np.squeeze(np.array(b))) / w[0, 1]
    plt.plot(x0, x1, color = 'y')
    plt.ylim((-10,12))
    plt.show()
dataToShow(dataList,labelList,b,alphas)
支持向量机SVM_第1张图片
output_7_0.png

完整版SMO算法

class optStructK:
    def __init__(self,dataMatIn, classLabels, C, toler):
        self.X = dataMatIn
        selef.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = np.zeros((self.m,1))
        self.b = 0
        self.eCache = np.zeros((self.m,2)) #误差缓存
#计算Ei
def calcEk(oS, k):
    fXk = float(np.dot((oS.alphas * oS.labelMat).T, np.dot(oS.X, oS.X[k:k+1,:].T))) + oS.b
    #计算Ej
    Ek = fXk - float(oS.labelMat[k])
    return Ek
#内循环选择alpha
def selectJK(i,oS,Ei):
    '''
    内循环选择alpha的启发式算法
    参数：
        i -- 外循环alpha的下标
        oS -- 类
        Ei -- 误差
    返回：
        j -- 选择alpha的下标
        Ej -- 误差
    '''
    #初始化
    maxK = -1;maxDeltaE = 0; Ej = 0
    oS.eCache[i] = [1,Ei]
    #选择合理的集合
    validEcacheList = np.nonzero(oS.eCache[:,0])[0]
    if (len(validEcacheList)) > 1:
        #选择最大步长的alpha
        for k in validEcacheList:
            #不重复计算
            if k == i: continue
            #计算误差
            Ek = calcEk(oS, k)
            #计算步长
            deltaE = abs(Ei - Ek)
            #记录最佳选择
            if (deltaE > maxDeltaE):
                maxK = k;maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    #没有合理值
    else:
        #随机选择
        j = select(i,oS.m)
        Ej = calcEk(oS,j)
    return j,Ej

def updateEkK(oS,k):
    #在alpha更新后存储计算得到的误差
    Ek = calcEk(oS,k)
    oS.eCache[k] = [1,Ek]
def innerLK(i, oS):
    #计算误差
    Ei = calcEkK(oS, i)
    #找出不满足KKT条件的alpha
    if ((oS.labelMat[i, 0]*Ei < -oS.tol) and (oS.alphas[i, 0] < oS.C)) or ((oS.labelMat[i, 0]*Ei > oS.tol) and (oS.alphas[i, 0] > 0)):
        #选择j
        j,Ej = selectJK(i, oS, Ei)
        #存储旧的值
        alphaIold = oS.alphas[i, 0].copy(); alphaJold = oS.alphas[j, 0].copy();
        #两种情况求边界值
        if (oS.labelMat[i, 0] != oS.labelMat[j, 0]):
            L = max(0, oS.alphas[j, 0] - oS.alphas[i, 0])
            H = min(oS.C, oS.C + oS.alphas[j, 0] - oS.alphas[i, 0])
        else:
            L = max(0, oS.alphas[j, 0] + oS.alphas[i, 0] - oS.C)
            H = min(oS.C, oS.alphas[j, 0] + oS.alphas[i, 0])
        if L==H: return 0
        #计算变化量
        eta = 2.0 * np.dot(oS.X[i:i+1,:], oS.X[j:j+1,:].T) - np.dot(oS.X[i:i+1,:], oS.X[i:i+1,:].T) - np.dot(oS.X[j:j+1,:], oS.X[j:j+1,:].T)
        if eta >= 0: return 0
        #更新alpha
        oS.alphas[j, 0] -= oS.labelMat[j, 0]*(Ei - Ej)/eta
        #约束alpha
        oS.alphas[j, 0] = clipAlpha(oS.alphas[j, 0],H,L)
        updateEkK(oS, j)
        if (abs(oS.alphas[j, 0] - alphaJold) < 0.00001): return 0
        oS.alphas[i, 0] += oS.labelMat[j, 0]*oS.labelMat[i, 0]*(alphaJold - oS.alphas[j, 0])
        updateEkK(oS, i)
        b1 = oS.b - Ei- oS.labelMat[i, 0]*(oS.alphas[i, 0]-alphaIold)*np.dot(oS.X[i:i+1,:], oS.X[i:i+1,:].T) - oS.labelMat[j, 0]*(oS.alphas[j, 0]-alphaJold)*np.dot(oS.X[i:i+1,:], oS.X[j:j+1,:].T)
        b2 = oS.b - Ej- oS.labelMat[i, 0]*(oS.alphas[i, 0]-alphaIold)*np.dot(oS.X[i:i+1,:], oS.X[j:j+1,:].T) - oS.labelMat[j, 0]*(oS.alphas[j, 0]-alphaJold)*np.dot(oS.X[j:j+1,:], oS.X[j:j+1,:].T)
        if (0 < oS.alphas[i, 0]) and (oS.C > oS.alphas[i, 0]): oS.b = b1
        elif (0 < oS.alphas[j, 0]) and (oS.C > oS.alphas[j, 0]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0
def smoPK(dataMatIn, classLabels, C, toler, maxIter):
    #建立类变量
    oS = optStructK(np.array(dataMatIn),np.array(classLabels).reshape(-1, 1),C,toler)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    #执行循环
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:
            #遍历所有
            for i in range(oS.m):        
                alphaPairsChanged += innerLK(i,oS)
                #print("fullSet, iter: {} i:{}, pairs changed {}".format(iter,i,alphaPairsChanged))
            iter += 1
        else:
            #遍历非边界值
            nonBoundIs = np.nonzero((oS.alphas > 0) * (oS.alphas < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerLK(i,oS)
                #print("non-bound, iter: {} i:{}, pairs changed {}".format(iter,i,alphaPairsChanged))
            iter += 1
        if entireSet: entireSet = False 
        elif (alphaPairsChanged == 0): entireSet = True  
        #print("iteration number: {}".format(iter))
    return oS.b,oS.alphas

dataList,labelList = loadData('../../Reference Code/Ch06/testSet.txt')
b, alphas = smoSimple(dataList, labelList, 0.6, 0.001, 40)
print('b= {}'.format(b))
print('（支持向量对应的alpha>0）alpha>0\n{}'.format(alphas[alphas>0]))

循环次数: 0 alpha:0, alpha对修改了 1 次
L==H
循环次数: 0 alpha:4, alpha对修改了 2 次
j not moving enough
循环次数: 0 alpha:6, alpha对修改了 3 次
L==H
j not moving enough
L==H
循环次数: 0 alpha:25, alpha对修改了 4 次
L==H
循环次数: 0 alpha:29, alpha对修改了 5 次
L==H
循环次数: 0 alpha:52, alpha对修改了 6 次
j not moving enough
循环次数: 0 alpha:55, alpha对修改了 7 次
L==H
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
循环次数: 0 alpha:52, alpha对修改了 1 次
j not moving enough
循环次数: 0 alpha:55, alpha对修改了 2 次
j not moving enough
j not moving enough
j not moving enough
j not moving enough
循环次数: 0 alpha:76, alpha对修改了 3 次
j not moving enough
L==H
L==H
迭代次数: 0
循环次数: 0 alpha:0, alpha对修改了 1 次
j not moving enough
j not moving enough
L==H
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
循环次数: 0 alpha:96, alpha对修改了 2 次
j not moving enough
迭代次数: 0
j not moving enough
j not moving enough
循环次数: 0 alpha:8, alpha对修改了 1 次
循环次数: 0 alpha:10, alpha对修改了 2 次
L==H
j not moving enough
j not moving enough
j not moving enough
L==H
L==H
循环次数: 0 alpha:54, alpha对修改了 3 次
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 0
j not moving enough
循环次数: 0 alpha:5, alpha对修改了 1 次
j not moving enough
j not moving enough
循环次数: 0 alpha:17, alpha对修改了 2 次
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
L==H
L==H
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
L==H
迭代次数: 0
j not moving enough
循环次数: 0 alpha:5, alpha对修改了 1 次
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
循环次数: 0 alpha:29, alpha对修改了 2 次
j not moving enough
循环次数: 0 alpha:52, alpha对修改了 3 次
循环次数: 0 alpha:54, alpha对修改了 4 次
j not moving enough
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 0
j not moving enough
j not moving enough
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
循环次数: 0 alpha:54, alpha对修改了 1 次
j not moving enough
j not moving enough
j not moving enough
循环次数: 0 alpha:86, alpha对修改了 2 次
L==H
L==H
j not moving enough
L==H
j not moving enough
迭代次数: 0
j not moving enough
j not moving enough
循环次数: 0 alpha:5, alpha对修改了 1 次
j not moving enough
j not moving enough
L==H
j not moving enough
j not moving enough
j not moving enough
j not moving enough


迭代次数: 38
j not moving enough
j not moving enough
j not moving enough
j not moving enough
迭代次数: 39
j not moving enough
j not moving enough
L==H
j not moving enough
迭代次数: 40
b= [-4.65074859]
（支持向量对应的alpha>0）alpha>0
[0.11699604 0.29638533 0.41338137]

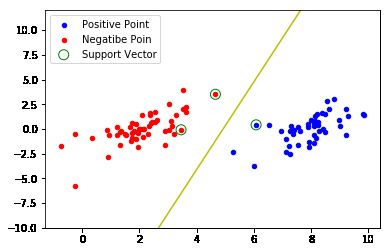
dataToShow(dataList,labelList,b,alphas)
支持向量机SVM_第2张图片
output_12_0.png

引入核函数

def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
    m,n = shape(X)
    K = mat(zeros((m,1)))
    if kTup[0]=='lin': K = X * A.T   #linear kernel
    elif kTup[0]=='rbf':
        for j in range(m):
            deltaRow = X[j,:] - A
            K[j] = np.dot(deltaRow, deltaRow.T)
        K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
    else: raise NameError('Houston We Have a Problem -- \
    That Kernel is not recognized')
    return K
class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters 
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) #first column is valid flag
        self.K = mat(zeros((self.m,self.m)))
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
def calcEk(oS, k):
    fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek
def selectJ(i, oS, Ei):         #this is the second choice -heurstic, and calcs Ej
    maxK = -1; maxDeltaE = 0; Ej = 0
    oS.eCache[i] = [1,Ei]  #set valid #choose the alpha that gives the maximum delta E
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:   #loop through valid Ecache values and find the one that maximizes delta E
            if k == i: continue #don't calc for i, waste of time
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:   #in this case (first time around) we don't have any valid eCache values
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]
def innerL(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: return 0
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
        if eta >= 0: return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS, j) #added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    #full Platt SMO
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:   #go over all
            for i in range(oS.m):        
                alphaPairsChanged += innerL(i,oS)
                #print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        else:#go over non-bound (railed) alphas
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                #print( "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        if entireSet: entireSet = False #toggle entire set loop
        elif (alphaPairsChanged == 0): entireSet = True  
        #print( "iteration number: %d" % iter)
    return oS.b,oS.alphas
def calcWs(alphas,dataArr,classLabels):
    X = mat(dataArr); labelMat = mat(classLabels).transpose()
    m,n = shape(X)
    w = zeros((n,1))
    for i in range(m):
        w += multiply(alphas[i]*labelMat[i],X[i,:].T)
    return w

测试

def testRbf(k1=1.3):
    dataArr,labelArr  = loadData('../../Reference Code/Ch06/testSetRBF.txt')
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=datMat[svInd] #get matrix of only support vectors
    labelSV = labelMat[svInd];
    print( "there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print( "the training error rate is: %f" % (float(errorCount)/m))
    dataArr,labelArr = loadData('../../Reference Code/Ch06/testSetRBF2.txt')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1    
    print( "the test error rate is: %f" % (float(errorCount)/m) )
    return b,alphas

import matplotlib.pyplot as plt
import numpy as np
def dataToShow(dataList,labelList,b,alphas):
    #array形式方便处理
    dataArray = np.array(dataList)
    alphasArray = np.array(alphas.tolist())
    #变成一列，-1表示自动计算多少行
    labelArray = np.array(labelList).reshape(-1,1)
    #正类负类分开画图,np.squeeze转化成一维的
    posData = dataArray[np.squeeze(labelArray>0.0)]    
    negData = dataArray[np.squeeze(labelArray<0.0)]
    svData = dataArray[np.squeeze(alphasArray>0.0)]
    plt.figure()
    plt.scatter(posData[:,0],posData[:,1],c='b',s=20)
    plt.scatter(negData[:,0],negData[:,1],c='r',s=20)
    plt.scatter(svData[:,0],svData[:,1],marker='o',c='',s=100,edgecolors='g')
    plt.legend(['Positive Point','Negatibe Poin','Support Vector'])
#     #画分割超平面
#     w = np.dot((alphasArray * labelArray).T, dataArray)
#     x0 = np.array([2, 8])
#     #分割线：w0*x0+w1*x1+b=0
#     x1 = -(w[0, 0] * x0 + np.squeeze(np.array(b))) / w[0, 1]
#     plt.plot(x0, x1, color = 'y')
#     plt.ylim((-10,12))
    plt.show()



dataList,labelList  = loadData('../../Reference Code/Ch06/testSetRBF.txt')

b,alphas = testRbf(k1=1.3)
dataToShow(dataList,labelList,b,alphas)

there are 29 Support Vectors
the training error rate is: 0.130000
the test error rate is: 0.150000
支持向量机SVM_第3张图片
output_19_1.png 
b,alphas = testRbf(k1=0.1)
dataToShow(dataList,labelList,b,alphas)

there are 84 Support Vectors
the training error rate is: 0.000000
the test error rate is: 0.090000
支持向量机SVM_第4张图片
output_20_1.png

手写识别

def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

def loadImages(dirName):
    from os import listdir
    hwLabels = []
    trainingFileList = listdir(dirName)           #load the training set
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        if classNumStr == 9: hwLabels.append(-1)
        else: hwLabels.append(1)
        trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
    return trainingMat, hwLabels    

def testDigits(kTup=('rbf', 10)):
    dataArr,labelArr = loadImages('../../../Week1/Reference Code/trainingDigits')
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=datMat[svInd] 
    labelSV = labelMat[svInd];
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m))
    dataArr,labelArr = loadImages('../../../Week1/Reference Code/testDigits')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1    
    print("the test error rate is: %f" % (float(errorCount)/m)) 

testDigits(('rbf', 20))

there are 204 Support Vectors
the training error rate is: 0.000000
the test error rate is: 0.010571

你可能感兴趣的:(支持向量机SVM)

  • 机器学习VS深度学习 nfgo 机器学习
    机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
  • 分类算法可视化方法 dundunmm 数据挖掘分类数据挖掘人工智能可视化
    可视化方法可以用于帮助理解分类算法的决策边界、性能和在不同数据集上的行为。下面列举几个常见的可视化方法。1.决策边界可视化这种方法用于可视化不同分类算法在二维特征空间中如何分隔不同类别。对于理解决策树、支持向量机（SVM）、逻辑回归和k近邻（k-NN）等模型的行为非常有用。importnumpyasnpimportmatplotlib.pyplotaspltfromsklearn.datasets
  • 时序预测|基于粒子群优化支持向量机的时间序列预测Matlab程序PSO-SVM 单变量和多变量 含基础模型 机器不会学习CL 智能优化算法时间序列预测支持向量机matlab算法
    时序预测|基于粒子群优化支持向量机的时间序列预测Matlab程序PSO-SVM单变量和多变量含基础模型文章目录一、基本原理1.问题定义2.数据准备3.SVM模型构建4.粒子群优化（PSO）5.优化与模型训练6.模型评估与预测7.流程总结8.MATLAB实现概述二、实验结果三、核心代码四、代码获取五、总结时序预测|基于粒子群优化支持向量机的时间序列预测Matlab程序PSO-SVM单变量和多变量含基
  • 【ML】支持向量机SVM及Python实现（详细） 2401_84009698 程序员支持向量机python算法
    fromsklearn.preprocessingimportStandardScalerfrommatplotlib.colorsimportListedColormapfromsklearn.svmimportSVC###2.1加载数据样本加载样本数据及其分类标签iris=datasets.load_iris()X=iris.data[:,[2,3]]#按花瓣划分#X=iris.data[:,
  • 鸿蒙原生开发——轻内核A核源码分析系列三 物理内存（2） OpenHarmony_小贾 鸿蒙开发HarmonyOSOpenHarmonyharmonyosopenharmony移动开发程序人生鸿蒙开发
    3.1.2.3函数OsVmPhysLargeAlloc当执行到这个函数时，说明空闲链表上的单个内存页节点的大小已经不能满足要求，超过了第9个链表上的内存页节点的大小了。⑴处计算需要申请的内存大小。⑵从最大的链表上进行遍历每一个内存页节点。⑶根据每个内存页的开始内存地址，计算需要的内存的结束地址，如果超过内存段的大小，则继续遍历下一个内存页节点。⑷处此时paStart表示当前内存页的结束地址，接下来
  • 鸿蒙轻内核A核源码分析系列四（3） 虚拟内存 OpenHarmony_小贾 OpenHarmonyHarmonyOS鸿蒙开发harmonyosOpenHarmony鸿蒙内核移动开发驱动开发系统开发
    4.2函数LOS_RegionAlloc函数LOS_RegionAlloc用于从地址空间中申请空闲的虚拟地址区间。参数较多，LosVmSpace*vmSpace指定虚拟地址空间，VADDR_Tvaddr指定虚拟地址，当为空时，从映射区申请虚拟地址；当不为空时，使用该虚拟地址。如果该虚拟地址已经被映射，会先相应的解除映射处理等。size_tlen指定要申请的地区区间的长度。UINT32regionF
  • Django Admin管理后台导入CSV 背着吉他去流浪 django服务器python
    修改管理模型，代码如下：classCsvImportForm(forms.Form):csv_file=forms.FileField()@admin.register(Hero)classHeroAdmin(admin.ModelAdmin,ExportCsvMixin):...change_list_template="entities/heroes_changelist.html"defge
  • TEE是Trusted Execution Environment 的解释 weixin_38503885
    TEE是TrustedExecutionEnvironment的缩写简称，是可信执行环境的简称，在目前移动安全领域，TEE默认就是指的基于ARMtrustzone技术的TEE，其实在芯片架构层面，TEE应该包含下面三部分：1.利用intelTXT或AMD的SVM均可提供TEE，即基于处理器CPU的特殊指令，提供动态信任根DRTM服务，为敏感应用或数据提供可信执行环境；2.利用ARMTrustZon
  • AI模型：追求全能还是专精？ Lill_bin 杂谈人工智能分布式zookeeper机器学习游戏
    AI模型简介人工智能（AI）模型是人工智能系统的核心，它们是经过训练的算法，能够执行特定的任务，如图像识别、自然语言处理、游戏玩法、预测分析等。AI模型的类型很多，可以根据其功能和应用场景进行分类。常见的AI模型类型包括：监督学习模型：这些模型通过训练数据集学习，数据集中包含了输入和对应的输出标签。例子包括决策树、支持向量机（SVM）、神经网络等。无监督学习模型：这些模型处理没有标签的数据，目的是
  • Python知识点：如何使用Python进行时间序列预测 杰哥在此 Python系列python开发语言编程面试
    使用Python进行时间序列预测是一个非常常见的任务，可以应用于各种领域，如金融市场预测、销售量预测、天气预报等。时间序列预测的方法有很多，包括统计方法（如ARIMA模型）、机器学习方法（如支持向量机、决策树）、以及深度学习方法（如LSTM网络）。下面是一个简单的时间序列预测流程示例，使用Python和pandas、numpy、以及statsmodels库来实现ARIMA模型的时间序列预测。1.导
  • 机器学习在医学中的应用 听忆. 机器学习人工智能
    边走、边悟迟早会好机器学习在医学中的应用是一个广泛且复杂的领域，涵盖了从基础研究到临床应用的多个方面。以下是一个万字总结的结构性思路，分章节深入探讨不同应用场景、技术方法、挑战与未来展望。1.引言背景与发展：介绍医学领域的数字化转型以及机器学习的兴起，探讨其在医学中的潜力。机器学习的基本概念：简要介绍机器学习的基本原理、分类（监督学习、非监督学习、强化学习等）和常用算法（如神经网络、支持向量机、随
  • 分类预测|基于鲸鱼优化WOA最小二乘支持向量机LSSVM的数据分类预测Matlab程序WOA-LSSVM 多特征输入多类别输出 机器不会学习CL 分类预测智能优化算法分类支持向量机matlab
    分类预测|基于鲸鱼优化WOA最小二乘支持向量机LSSVM的数据分类预测Matlab程序WOA-LSSVM多特征输入多类别输出文章目录一、基本原理1.最小二乘支持向量机（LSSVM）LSSVM的基本步骤：2.鲸鱼优化算法（WOA）WOA的基本步骤：3.WOA-LSSVM的结合流程结合的流程如下：总结二、实验结果三、核心代码四、代码获取五、总结分类预测|基于鲸鱼优化WOA最小二乘支持向量机LSSVM的
  • 【HarmonyOS NEXT应用开发】案例103：基于JSVM创建引擎执行JS代码并销毁 青少年编程作品集 javascriptmicrosoft开发语言华为云harmonyos华为华为od
    场景描述通过JSVM，可以在应用运行期间直接执行一段动态加载的JS代码。也可以选择将一些对性能、底层系统调用有较高要求的核心功能用C/C++实现并将C++方法注册到JS侧，在JS代码中直接调用，提高应用的执行效率。功能描述通过createJsCore方法来创建一个新的JS基础运行时环境，并通过该方法获得一个虚拟机ID，通过evalUateJS方法使用虚拟机ID对应的运行环境来运行JS代码，在JS代
  • 自然语言处理系列五十》文本分类算法》SVM支持向量机算法原理 陈敬雷-充电了么-CEO兼CTO 算法大数据人工智能算法自然语言处理分类nlpai人工智能chatgpt
    注：此文章内容均节选自充电了么创始人，CEO兼CTO陈敬雷老师的新书《自然语言处理原理与实战》（人工智能科学与技术丛书）【陈敬雷编著】【清华大学出版社】文章目录自然语言处理系列五十SVM支持向量机》算法原理SVM支持向量机》代码实战总结自然语言处理系列五十SVM支持向量机》算法原理SVM支持向量机在文本分类的应用场景中，相比其他机器学习算法有更好的效果。下面介绍其原理，并用SparkMLlib机器
  • 鸿蒙（API 12 Beta2版）NDK开发【JSVM-API简介】 移动开发技术栈 鸿蒙开发harmonyos华为鸿蒙系统鸿蒙NDK模块加载jsvm
    JSVM-API简介场景介绍HarmonyOSJSVM-API是基于标准JS引擎提供的一套稳定的ABI，为开发者提供了较为完整的JS引擎能力，包括创建和销毁引擎，执行JS代码，JS/C++交互等关键能力。通过JSVM-API，开发者可以在应用运行期间直接执行一段动态加载的JS代码。也可以选择将一些对性能、底层系统调用有较高要求的核心功能用C/C++实现并将C++方法注册到JS侧，在JS代码中直接调
  • HarmonyOS开发规范：JSVM-API接口总结 冲浪王子_浪浪 HarmonyOSOpenHarmony鸿蒙开发前端鸿蒙华为harmonyoshtml移动开发鸿蒙系统
    JSVM_Status是一个枚举数据类型，表示JSVM-API接口返回的状态信息。每当调用一个JSVM-API函数，都会返回该值，表示操作成功与否的相关信息。typedefenum{JSVM_OK,JSVM_INVALID_ARG,JSVM_OBJECT_EXPECTED,JSVM_STRING_EXPECTED,JSVM_NAME_EXPECTED,JSVM_FUNCTION_EXPECTED,
  • 深度学习100问13:什么是二分类问题 不断持续学习ing 人工智能机器学习自然语言处理
    嘿，你知道二分类问题不？这就像是一个“超级裁判”，要把东西分成两大类。一、定义及举例想象一下，生活中有很多时候我们得决定一个东西到底属于哪一边。就像判断一封邮件，是“垃圾邮件”呢，还是“正常邮件”；或者看看一个病人，是“得了某种病”呢，还是“没得病”。二、解决方法要解决二分类问题呀，我们可以找来一些“魔法工具”，也就是机器学习算法。像逻辑回归啦、支持向量机啦、决策树啦等等。这些算法就像聪明的小助手
  • 每天一个数据分析题（五百一十二）- 数据标准化 跟着紫枫学姐学CDA 数据分析题库数据分析数据挖掘
    在完整的机器学习流程中，数据标准化（DataStandardization）一直是一项重要的处理流程。不同模型对于数据是否标准化的敏感程度不同，以下哪个模型对变量是否标准化不敏感？A.决策树B.KNNC.K-MeansD.SVM数据分析认证考试介绍：点击进入题目来源于CDA模拟题库点击此处获取答案数据分析专项练习题库内容涵盖Python，SQL，统计学，数据分析理论，深度学习，可视化，机器学习，S
  • 回归预测|基于卷积神经网络-鲸鱼优化-最小二乘支持向量机的数据回归预测Matlab程序 CNN-WOA-LSSVM 机器不会学习CL 回归预测智能优化算法回归cnn支持向量机
    回归预测|基于卷积神经网络-鲸鱼优化-最小二乘支持向量机的数据回归预测Matlab程序CNN-WOA-LSSVM文章目录一、基本原理1.数据预处理2.特征提取（CNN）3.参数优化（WOA）4.模型训练（LSSVM）5.模型评估和优化6.预测总结二、实验结果三、核心代码四、代码获取五、总结回归预测|基于卷积神经网络-鲸鱼优化-最小二乘支持向量机的数据回归预测Matlab程序CNN-WOA-LSSV
  • 机器学习：svm算法原理的优缺点和适应场景 夜清寒风 支持向量机算法机器学习
    1、概述：基本原理：间隔（Margin）：SVM试图找到一个超平面，这个超平面不仅能够区分不同的类别，而且具有最大的间隔。间隔是数据点到超平面的最近距离。支持向量（SupportVectors）：这些是距离超平面最近的数据点，它们决定了超平面的位置和方向。支持向量机（SVM）是一种在机器学习领域广泛使用的监督学习模型，它通过找到数据点之间的最优超平面来进行分类或回归分析。以下是SVM算法的一些优缺
  • 深度学习速通系列:贝叶思&SVM Ven% 支持向量机人工智能深度学习算法机器学习
    贝叶斯（Bayesian）方法和支持向量机（SVM，SupportVectorMachine）是两种不同的机器学习算法，它们在解决分类和回归问题时有着不同的原理和应用场景贝叶斯方法：贝叶斯方法基于贝叶斯定理，这是一种利用已知信息（先验概率）来预测未知事件（后验概率）的概率方法。它通常用于分类问题，特别是当数据集较小或存在类别不平衡时。贝叶斯方法可以处理不确定性，并且可以通过增加新的数据来更新先验概
  • 【ShuQiHere】《机器学习的进化史『下』：从神经网络到深度学习的飞跃》 ShuQiHere 机器学习深度学习神经网络
    【ShuQiHere】引言：神经网络与深度学习的兴起在上篇文章中，我们回顾了机器学习的起源与传统模型的发展历程，如线性回归、逻辑回归和支持向量机（SVM）。然而，随着数据规模的急剧增长和计算能力的提升，传统模型在处理复杂问题时显得力不从心。在这种背景下，神经网络重新进入了研究者们的视野，并逐步演变为深度学习，成为解决复杂问题的强大工具。今天，我们将进一步探索从神经网络到深度学习的进化历程，揭示这些
  • 使用SVM进行评论情感分析 github_czy 支持向量机机器学习人工智能
    importpandasaspdfromsklearn.model_selectionimporttrain_test_splitfromsklearn.feature_extraction.textimportTfidfVectorizerfromsklearn.svmimportSVCfromsklearn.metricsimportaccuracy_score,precision_score
  • 智能优化特征选择|基于鹦鹉优化（2024年新出优化算法）的特征选择（分类器选用的是SVM）研究Matlab程序 【优化算法可以替换成其他优化方法】 机器不会学习CL 智能优化算法智能优化特征选择算法支持向量机matlab
    智能优化特征选择|基于鹦鹉优化（2024年新出优化算法）的特征选择（分类器选用的是SVM）研究Matlab程序【优化算法可以替换成其他优化方法】文章目录一、PO基本原理基本原理基本流程示例应用二、实验结果三、核心代码四、代码获取五、总结智能优化特征选择|基于鹦鹉优化（2024年新出优化算法）的特征选择（分类器选用的是SVM）研究Matlab程序【优化算法可以替换成其他优化方法】一、PO基本原理鹦鹉
  • 机器学习——支持向量机 酱香编程，风雨兼程 机器学习支持向量机机器学习算法
    一、间隔与支持向量  给定训练样本集D={(x1,y1),(x2,y2),⋯ ,(xm,ym)},yi∈{−1,+1}D=\{(\bmx_1,y_1),(\bmx_2,y_2),\cdots,(\bmx_m,y_m)\},y_i\in\{-1,+1\}D={(x1,y1),(x2,y2),⋯,(xm,ym)},yi∈{−1,+1}，分类学习最基本的想法就是基于训练集DDD在样本空间中找到一个划分超
  • KVM虚拟机命令行常用操作 文静小土豆 linux运维redis
    1，首先验证CPU是否支持虚拟化，输入有vmx或svm就支持，支持虚拟化则就支持KVMcat/proc/cpuinfo|egrep'vmx|svm'2，查看KVM模块是否加载lsmod|grepkvm#kvm_intel1700860#kvm5663401kvm_intel#irqbypass135031kvm3，安装KVM虚拟机yum-yinstallqemu-kvmqemu-imglibvir
  • 回归预测|基于北方苍鹰优化支持向量机的数据回归预测Matlab程序NGO-SVM 多特征输入单输出 高引用先用先创新 机器不会学习CL 回归预测智能优化算法回归支持向量机matlab
    回归预测|基于北方苍鹰优化支持向量机的数据回归预测Matlab程序NGO-SVM多特征输入单输出高引用先用先创新文章目录前言回归预测|基于北方苍鹰优化支持向量机的数据回归预测Matlab程序NGO-SVM多特征输入单输出高引用先用先创新一、NGO-SVM模型1.北方苍鹰优化算法（NGO）的原理2.支持向量机（SVM）的原理3.NGO-SVM回归预测模型的结合总结二、实验结果三、核心代码四、代码获取
  • python库——sklearn的关键组件和参数设置 零 度° pythonpythonsklearn
    文章目录模型构建线性回归逻辑回归决策树分类器随机森林支持向量机K-近邻模型评估交叉验证性能指标特征工程主成分分析标准化和归一化scikit-learn，简称sklearn，是Python中一个广泛使用的机器学习库，它建立在NumPy、SciPy和Matplotlib这些科学计算库之上。sklearn提供了简单而有效的工具来进行数据挖掘和数据分析。我们将介绍sklearn中一些关键组件的参数设置。模
  • 四十一、【人工智能】【机器学习】- Bayesian Logistic Regression算法模型 暴躁的大熊 人工智能人工智能机器学习算法
    系列文章目录第一章【机器学习】初识机器学习第二章【机器学习】【监督学习】-逻辑回归算法(LogisticRegression)第三章【机器学习】【监督学习】-支持向量机(SVM)第四章【机器学习】【监督学习】-K-近邻算法(K-NN)第五章【机器学习】【监督学习】-决策树(DecisionTrees)第六章【机器学习】【监督学习】-梯度提升机(GradientBoostingMachine,GBM
  • 【机器学习理论基础】一文看尽朴素贝叶斯算法 大数据AI MachineLearning机器学习
    在所有的机器学习分类算法中，朴素贝叶斯和其他绝大多数的分类算法都不同。对于大多数的分类算法，比如决策树,KNN,逻辑回归，支持向量机等，他们都是判别方法，也就是直接学习出特征输出Y和特征X之间的关系，要么是决策函数Y=f(X)Y=f(X)Y=f(X),要么是条件分布P(Y∣X)P(Y|X)P(Y∣X)。但是朴素贝叶斯却是生成方法，也就是直接找出特征输出YYY和特征XXX的联合分布P(X,Y)P(X
  • 深入浅出Java Annotation(元注解和自定义注解） Josh_Persistence Java Annotation元注解自定义注解
    一、基本概述     　　 Annontation是Java5开始引入的新特征。中文名称一般叫注解。它提供了一种安全的类似注释的机制，用来将任何的信息或元数据（metadata）与程序元素（类、方法、成员变量等）进行关联。   　　更通俗的意思是为程序的元素（类、方法、成员变量）加上更直观更明了的说明，这些说明信息是与程序的业务逻辑无关，并且是供指定的工具或
  • mysql优化特定类型的查询 annan211 java工作mysql
    本节所介绍的查询优化的技巧都是和特定版本相关的，所以对于未来mysql的版本未必适用。 1 优化count查询 对于count这个函数的网上的大部分资料都是错误的或者是理解的都是一知半解的。在做优化之前我们先来看看 真正的count()函数的作用到底是什么。 count()是一个特殊的函数，有两种非常不同的作用，他可以统计某个列值的数量，也可以统计行数。 在统
  • MAC下安装多版本JDK和切换几种方式 棋子chessman jdk
    环境： MAC AIR,OS X 10.10,64位   历史： 过去 Mac 上的 Java 都是由 Apple 自己提供，只支持到 Java 6，并且OS X 10.7 开始系统并不自带（而是可选安装）（原自带的是1.6）。 后来 Apple 加入 OpenJDK 继续支持 Java 6，而 Java 7 将由 Oracle 负责提供。   在终端中输入jav
  • javaScript （1） Array_06 JavaScriptjava浏览器
    JavaScript 1、运算符 　　运算符就是完成操作的一系列符号，它有七类： 　　赋值运算符（=,+=,-=,*=,/=,%=,<<=,>>=,|=,&=）、算术运算符(+,-,*,/,++,--,%)、比较运算符(>,<,<=,>=,==,===,!=,!==)、逻辑运算符(||,&&,!)、条件运算(?:)、位
  • 国内顶级代码分享网站 袁潇含 javajdkoracle.netPHP
           现在国内很多开源网站感觉都是为了利益而做的                  当然利益是肯定的,否则谁也不会免费的去做网站      &
  • Elasticsearch、MongoDB和Hadoop比较 随意而生 mongodbhadoop搜索引擎
      IT界在过去几年中出现了一个有趣的现象。很多新的技术出现并立即拥抱了“大数据”。稍微老一点的技术也会将大数据添进自己的特性，避免落大部队太远，我们看到了不同技术之间的边际的模糊化。假如你有诸如Elasticsearch或者Solr这样的搜索引擎，它们存储着JSON文档，MongoDB存着JSON文档，或者一堆JSON文档存放在一个Hadoop集群的HDFS中。你可以使用这三种配
  • mac os 系统科研软件总结 张亚雄 mac os
    1.1 Microsoft Office for Mac 2011      大客户版，自行搜索。      1.2 Latex （MacTex）:      系统环境：https://tug.org/mactex/     &nb
  • Maven实战（四）生命周期 AdyZhang maven
    1. 三套生命周期     Maven拥有三套相互独立的生命周期，它们分别为clean，default和site。 每个生命周期包含一些阶段，这些阶段是有顺序的，并且后面的阶段依赖于前面的阶段，用户和Maven最直接的交互方式就是调用这些生命周期阶段。 以clean生命周期为例，它包含的阶段有pre-clean, clean 和 post
  • Linux下Jenkins迁移 aijuans Jenkins
    1. 将Jenkins程序目录copy过去      源程序在/export/data/tomcatRoot/ofctest-jenkins.jd.com下面            tar -cvzf jenkins.tar.gz ofctest-jenkins.jd.com &
  • request.getInputStream()只能获取一次的问题 ayaoxinchao requestInputstream
    问题：在使用HTTP协议实现应用间接口通信时，服务端读取客户端请求过来的数据，会用到request.getInputStream()，第一次读取的时候可以读取到数据，但是接下来的读取操作都读取不到数据   原因： 1. 一个InputStream对象在被读取完成后，将无法被再次读取，始终返回-1； 2. InputStream并没有实现reset方法（可以重
  • 数据库SQL优化大总结之 百万级数据库优化方案 BigBird2012 SQL优化
    网上关于SQL优化的教程很多，但是比较杂乱。近日有空整理了一下，写出来跟大家分享一下，其中有错误和不足的地方，还请大家纠正补充。 这篇文章我花费了大量的时间查找资料、修改、排版，希望大家阅读之后，感觉好的话推荐给更多的人，让更多的人看到、纠正以及补充。 1.对查询进行优化，要尽量避免全表扫描，首先应考虑在 where 及 order by 涉及的列上建立索引。 2.应尽量避免在 where
  • jsonObject的使用 bijian1013 javajson
            在项目中难免会用java处理json格式的数据，因此封装了一个JSONUtil工具类。 JSONUtil.java package com.bijian.json.study; import java.util.ArrayList; import java.util.Date; import java.util.HashMap;
  • [Zookeeper学习笔记之六]Zookeeper源代码分析之Zookeeper.WatchRegistration bit1129 zookeeper
    Zookeeper类是Zookeeper提供给用户访问Zookeeper service的主要API，它包含了如下几个内部类     首先分析它的内部类，从WatchRegistration开始，为指定的znode path注册一个Watcher，   /** * Register a watcher for a particular p
  • 【Scala十三】Scala核心七：部分应用函数 bit1129 scala
    何为部分应用函数？ Partially applied function: A function that’s used in an expression and that misses some of its arguments.For instance, if function f has type Int => Int => Int, then f and f(1) are p
  • Tomcat Error listenerStart 终极大法 ronin47 tomcat
    Tomcat报的错太含糊了，什么错都没报出来，只提示了Error listenerStart。为了调试，我们要获得更详细的日志。可以在WEB-INF/classes目录下新建一个文件叫logging.properties，内容如下 Java代码  handlers = org.apache.juli.FileHandler, java.util.logging.ConsoleHa
  • 不用加减符号实现加减法 BrokenDreams 实现
            今天有群友发了一个问题，要求不用加减符号(包括负号)来实现加减法。         分析一下，先看最简单的情况，假设1+1，按二进制算的话结果是10，可以看到从右往左的第一位变为0，第二位由于进位变为1。    
  • 读《研磨设计模式》-代码笔记-状态模式-State bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ /* 当一个对象的内在状态改变时允许改变其行为，这个对象看起来像是改变了其类 状态模式主要解决的是当控制一个对象状态的条件表达式过于复杂时的情况 把状态的判断逻辑转移到表示不同状态的一系列类中，可以把复杂的判断逻辑简化 如果在
  • CUDA程序block和thread超出硬件允许值时的异常 cherishLC CUDA
    调用CUDA的核函数时指定block 和 thread大小，该大小可以是dim3类型的（三维数组），只用一维时可以是usigned int型的。 以下程序验证了当block或thread大小超出硬件允许值时会产生异常！！！GPU根本不会执行运算！！！ 所以验证结果的正确性很重要！！！ 在VS中创建CUDA项目会有一个模板，里面有更详细的状态验证。 以下程序在K5000GPU上跑的。
  • 诡异的超长时间GC问题定位 chenchao051 jvmcmsGChbaseswap
    HBase的GC策略采用PawNew+CMS, 这是大众化的配置，ParNew经常会出现停顿时间特别长的情况，有时候甚至长到令人发指的地步，例如请看如下日志： 2012-10-17T05:54:54.293+0800: 739594.224: [GC 739606.508: [ParNew: 996800K->110720K(996800K), 178.8826900 secs] 3700
  • maven环境快速搭建 daizj 安装mavne环境配置
    一 下载maven 安装maven之前，要先安装jdk及配置JAVA_HOME环境变量。这个安装和配置java环境不用多说。 maven下载地址：http://maven.apache.org/download.html，目前最新的是这个apache-maven-3.2.5-bin.zip，然后解压在任意位置，最好地址中不要带中文字符，这个做java 的都知道，地址中出现中文会出现很多
  • PHP网站安全，避免PHP网站受到攻击的方法 dcj3sjt126com PHP
    对于PHP网站安全主要存在这样几种攻击方式:1、命令注入(Command Injection)2、eval注入(Eval Injection)3、客户端脚本攻击(Script Insertion)4、跨网站脚本攻击(Cross Site Scripting, XSS)5、SQL注入攻击(SQL injection)6、跨网站请求伪造攻击(Cross Site Request Forgerie
  • yii中给CGridView设置默认的排序根据时间倒序的方法 dcj3sjt126com GridView
    public function searchWithRelated() {         $criteria = new CDbCriteria;         $criteria->together = true; //without th
  • Java集合对象和数组对象的转换 dyy_gusi java集合
        在开发中，我们经常需要将集合对象（List，Set）转换为数组对象，或者将数组对象转换为集合对象。Java提供了相互转换的工具，但是我们使用的时候需要注意，不能乱用滥用。 1、数组对象转换为集合对象     最暴力的方式是new一个集合对象，然后遍历数组，依次将数组中的元素放入到新的集合中，但是这样做显然过
  • nginx同一主机部署多个应用 geeksun nginx
    近日有一需求，需要在一台主机上用nginx部署2个php应用，分别是wordpress和wiki，探索了半天，终于部署好了，下面把过程记录下来。 1.   在nginx下创建vhosts目录，用以放置vhost文件。 mkdir vhosts   2.   修改nginx.conf的配置， 在http节点增加下面内容设置，用来包含vhosts里的配置文件 #
  • ubuntu添加admin权限的用户账号 hongtoushizi ubuntuuseradd
    ubuntu创建账号的方式通常用到两种：useradd 和adduser . 本人尝试了useradd方法，步骤如下： 1:useradd    使用useradd时，如果后面不加任何参数的话，如：sudo useradd sysadm 创建出来的用户将是默认的三无用户：无home directory ,无密码,无系统shell。 顾应该如下操作：  
  • 第五章 常用Lua开发库2-JSON库、编码转换、字符串处理 jinnianshilongnian nginxlua
      JSON库   在进行数据传输时JSON格式目前应用广泛，因此从Lua对象与JSON字符串之间相互转换是一个非常常见的功能；目前Lua也有几个JSON库，本人用过cjson、dkjson。其中cjson的语法严格（比如unicode \u0020\u7eaf），要求符合规范否则会解析失败（如\u002），而dkjson相对宽松，当然也可以通过修改cjson的源码来完成
  • Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解 yaerfeng1989 timerquartz定时器
    原创整理不易，转载请注明出处：Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解 代码下载地址：http://www.zuidaima.com/share/1772648445103104.htm 有两种流行Spring定时器配置：Java的Timer类和OpenSymphony的Quartz。 1.Java Timer定时 首先继承jav
  • Linux下df与du两个命令的差别？ pda158 linux
    　一、df显示文件系统的使用情况，与du比較，就是更全盘化。 　　最经常使用的就是 df -T，显示文件系统的使用情况并显示文件系统的类型。 　　举比例如以下： 　　[root@localhost ~]# df -T 　　Filesystem                   Type &n
  • [转]SQLite的工具类 ---- 通过反射把Cursor封装到VO对象 ctfzh VOandroidsqlite反射Cursor
    在写DAO层时，觉得从Cursor里一个一个的取出字段值再装到VO(值对象)里太麻烦了，就写了一个工具类，用到了反射，可以把查询记录的值装到对应的VO里，也可以生成该VO的List。   使用时需要注意： 考虑到Android的性能问题，VO没有使用Setter和Getter，而是直接用public的属性。 表中的字段名需要和VO的属性名一样，要是不一样就得在查询的SQL中
  • 该学习笔记用到的Employee表 vipbooks oraclesql工作
        这是我在学习Oracle是用到的Employee表，在该笔记中用到的就是这张表，大家可以用它来学习和练习。 drop table Employee; -- 员工信息表 create table Employee( -- 员工编号 EmpNo number(3) primary key, -- 姓
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他