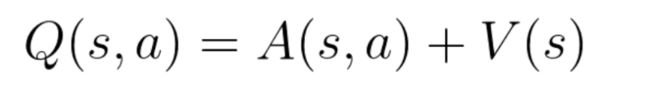本文为 AI 研习社编译的技术博客,原标题 :
Improvements in Deep Q Learning: Dueling Double DQN, Prioritized Experience Replay, and fixed Q-targets
作者 | Thomas Simonini
翻译 | 斯蒂芬•二狗子
校对 | 邓普斯•杰弗 整理 | 菠萝妹
原文链接:
https://medium.freecodecamp.org/improvements-in-deep-q-learning-dueling-double-dqn-prioritized-experience-replay-and-fixed-58b130cc5682
深度强化学习从入门到大师:进一步了解深度Q学习
(第三部分续)*
本文是Tensorflow的深度强化学习课程的一部分。原文查看教学大纲。
我们正在使用Tensorflow制作深度强化学习课程的视频版本,我们专注于实现部分,您可以查看 播放列表。
在我们上一篇关于 使用Tensorflow进行深度Q学习的文章中,我们实现了一个智能体,其可以学习玩简单版Doom。在视频版本中, 我们训练了一个玩太空入侵者的DQN智能体。
但是,在训练期间,我们发现存在很多变化。
深度Q-Learning于2014年提出。从那时起,已经进行了许多改进。所以,今天我们将看到四种策略可以显著 - 改善 - 训练和DQN智能体的结果:
fixed Q-targets
double DQNs
duelingDQN(又名 DDQN)
Prioritized Experience Replay(又名PER)
我们将实现一个智能体,可以学习玩Doom Deadly corridor。我们的人工智能必须走向基本目标(vest),并确保他们通过杀死敌人同时生存。
固定Q目标
理论
我们在Deep Q Learning文章中看到, 我们可通过计算TD目标值(Q_target)和当前Q值(Q的估计)之差 得到TD误差(又称损失)。
但真实的TD目标值我们并不知道。我们需要估计它。使用Bellman方程,我们看到TD目标只是在该状态下采取该行动的奖励加上下一个状态的折扣率下的最高Q值。
然而,问题是我们使用相同的参数(权重)来估计目标和Q值。结果是,TD目标与我们正在改变的参数(w)之间存在很大的相关性。
因此,这意味着在训练的每一步,我们的Q值都会发生变化,但目标值也会发生变化。所以,我们可以越来越接近我们的目标,但目标也在不断变化。这就像追逐一个移动的目标!这导致了训练的大振荡。
这就像你是一个牛仔(Q估计),你想抓住牛(Q目标),你必须更接近(减少错误)。
在每个时间步,你都试图接近牛,牛也会在每个时间步移动(因为你使用相同的参数)。
这导致了一种非常奇怪的追逐路径(训练中的大振荡)。
相反,我们可以使用DeepMind引入的固定Q-targets的想法:
使用具有固定参数的单独网络(让我们称之为w-)来估计TD目标。
在每个Tau步骤,我们从DQN网络复制参数以更新目标网络。
感谢这个程序改进,因为目标函数保持固定一段时间,将有更稳定的学习过程。
履行实现
实现固定的q-targets非常简单:
首先,我们创建两个网络(DQNetwork, TargetNetwork)
然后,我们创建一个函数,它将获取我们的 DQNetwork 参数并将它们复制到我们的 TargetNetwork
最后,在训练期间,我们使用目标网络计算TD目标。我们用DQNetwork 每一步 tau更新目标网络 (tau 是我们定义的超参数)。
Double DQNs
理论
Hado van Hasselt 介绍了Double DQNs, 或 double Learning 。该方法解决了Q值估计过高的问题。
要了解此问题,请记住我们如何计算TD Target:
通过计算TD目标,我们面临一个简单的问题:我们如何确定下一个状态的最佳动作是具有最高Q值的动作?
我们知道q值的准确性取决于智能体尝试了多少行动以及我们探索的邻近状态。
在训练开始时,智能体没有足够的信息来了解最佳行动。因此,将(有噪声的)最大q值作为最佳动作可能会导致false positives(FP,假正)。如果未优化的动作经常给出比所求得的最优化动作更高的Q值,则学习将变得困难。
解决方案是:当我们计算Q目标时,我们使用两个网络将动作选择与目标Q值生成分离:
使用 DQN 网络 选择对下一个状态采取的最佳动作(具有最高Q值)。
使用 目标网络 计算在下一个状态下执行该操作的目标Q值。
因此,Double DQN 帮助我们减少对q值的过高估计,从而帮助我们更快地训练并获得更稳定的学习。
实现
基于竞争构架Q网络 DuelingDQN(DDQN)
理论
请记住,Q值(Q(s,a))表示状态 s 下采取行动 a 。
所以我们可以将Q(s,a)分解为:
V(s):处于该状态s的值
A(s,a):在该状态s下采取该行动a的优势(该状态的采取此行动与所有其他可能行动相比有多好)。
在DDQN中,我们希望通过两个流streams得到 V(s) 、A(s,a)这两个参数的估计量:
一个是状态值 V(s)的估计
一个是每个动作的优势的估计 A(s,a)
然后,通过一个特殊的整合层将这两个流组合起来得到 Q(s,a)的估计值。
等下?但是,为什么我们需要分别计算这两个参数呢?
通过解耦估计,我们的DDQN可以直观地了解哪些状态是(或不是)有价值的,而不必了解每个状态下每个动作的效果(因此,还是需要计算V(s)的)。
使用原版的 DQN,需要计算某个状态state下每个动作的值。但如果该状态state不好,这样就做有什么意义呢?如果这个状态会导致智能体角色死亡,那么计算该状态(死亡状态的)的所有行动就没有意义。
因此,通过解耦计算 V(s),找出对于那些任何行为都不会被影响的状态尤其有用。在这种情况下,不必计算每个动作的值。例如,向右或向左移动仅在存在碰撞风险时才去关注。而且,在大多数状态下,无论选择何种行动,对发生的事情没有任何影响。
如果我们看论文Dueling Network Architectures for Deep Reinforcement Learning中的例子,会理解地更加清晰。
我们看到这种价值流Value network streams(V(s))是关注路面(橙色模糊),但更关注的是最前方地平线处是否有汽车出现。同时,该网络也注重得分。
另一方面,在右边第一帧图中,优势流the advantage stream(A(s,a))并没有太多关注道路,因为前面没有车(因此选择什么动作实际是无关紧要的)。但是,在第二帧图会引起它的注意,因为在前面有一辆汽车,并且对行动做出选择是至关重要且(与将要对发生的事情)非常相关的。
(译者注:V(s)关注于地平线上是否有车辆出现(此时动作的选择影响不大)以及分数;A(s,a) 则更关心会立即造成碰撞的车辆,此时动作的选择很重要。)
关于整合层aggregation layer,我们想得到该状态s下的每个动作的Q值。我们可能想将2个流组合成:
(注:其中 θ 是卷积层参数,β 和 α 是两支路全连接层参数。)
但如果这样做,我们将陷入可识别性问题,即 - 给定Q(s,a)我们无法找到A(s,a)和 V(s)。
并且无法找到给定Q(s,a)的V(s)和A(s,a),将在反向传播的过程中出现问题。为了避免这个问题,我们可以强制我们的优势函数在选中的行动上具有0优势。
(译者注:也就是保证该状态下各种动作的优势函数大小排序关系不变的前提下,缩小Q值范围,去均值的过程)
为此,我们减去了该状态下可能采取的所有行动优势的平均值。
因此,这种架构architecture 有助于加速训练网络。只计算状态的值,而不用计算该状态下所有动作的值。它可以帮助我们通过解耦两个流之间的估计来为每个动作找到更可靠的Q值。
实现
唯一要做的就是通过添加这些新的流streams来修改DQN架构:
class DDDQNNet:
def __init__(self, state_size, action_size, learning_rate, name):
self.state_size = state_size
self.action_size = action_size
self.learning_rate = learning_rate
self.name = name
# 使用 tf.variable_scope 了解具体用了什么网络模型 (DQN or target_net)
# it will be useful when we will update our w- parameters (by copy the DQN parameters)
with tf.variable_scope(self.name):
# 创建 the placeholders(占位)
# *state_size means that we take each elements of state_size in tuple hence is like if we wrote
# [None, 100, 120, 4]
self.inputs_ = tf.placeholder(tf.float32, [None, *state_size], name="inputs")
self.actions_ = tf.placeholder(tf.float32, [None, action_size], name="actions_")
# Remember that target_Q is the R(s,a) + ymax Qhat(s', a')
self.target_Q = tf.placeholder(tf.float32, [None], name="target")
"""
First convnet: 第一个卷积层
CNN
ELU 激活函数
"""
# Input is 100x120x4
self.conv1 = tf.layers.conv2d(inputs = self.inputs_,
filters = 32,
kernel_size = [8,8],
strides = [4,4],
padding = "VALID",
kernel_initializer=tf.contrib.layers.xavier_initializer_conv2d(),
name = "conv1")
self.conv1_out = tf.nn.elu(self.conv1, name="conv1_out")
"""
Second convnet:第二个卷积层
CNN
ELU
"""
self.conv2 = tf.layers.conv2d(inputs = self.conv1_out,
filters = 64,
kernel_size = [4,4],
strides = [2,2],
padding = "VALID",
kernel_initializer=tf.contrib.layers.xavier_initializer_conv2d(),
name = "conv2")
self.conv2_out = tf.nn.elu(self.conv2, name="conv2_out")
"""
Third convnet:第三个卷积层
CNN
ELU
"""
self.conv3 = tf.layers.conv2d(inputs = self.conv2_out,
filters = 128,
kernel_size = [4,4],
strides = [2,2],
padding = "VALID",
kernel_initializer=tf.contrib.layers.xavier_initializer_conv2d(),
name = "conv3")
self.conv3_out = tf.nn.elu(self.conv3, name="conv3_out")
self.flatten = tf.layers.flatten(self.conv3_out)
## 这里分出两个流 Here we separate into two streams
# 其中一个用来计算 V(s) -状态值函数
self.value_fc = tf.layers.dense(inputs = self.flatten,
units = 512,
activation = tf.nn.elu,
kernel_initializer=tf.contrib.layers.xavier_initializer(),
name="value_fc")
self.value = tf.layers.dense(inputs = self.value_fc,
units = 1,
activation = None,
kernel_initializer=tf.contrib.layers.xavier_initializer(),
name="value")
# 另一个流计算 A(s,a) -动作优势函数
self.advantage_fc = tf.layers.dense(inputs = self.flatten,
units = 512,
activation = tf.nn.elu,
kernel_initializer=tf.contrib.layers.xavier_initializer(),
name="advantage_fc")
self.advantage = tf.layers.dense(inputs = self.advantage_fc,
units = self.action_size,
activation = None,
kernel_initializer=tf.contrib.layers.xavier_initializer(),
name="advantages")
# Agregating layer 整合层
# Q(s,a) = V(s) + (A(s,a) - 1/|A| * sum A(s,a'))
self.output = self.value + tf.subtract(self.advantage, tf.reduce_mean(self.advantage, axis=1, keepdims=True))
# 这个 Q 是模型对 Q值 的预测值
self.Q = tf.reduce_sum(tf.multiply(self.output, self.actions_), axis=1)
# 这个损失函数loss是预测Q值(Q_values)和Q目标(Q_target)的差
# Sum(Qtarget - Q)^2 求平方和
self.loss = tf.reduce_mean(tf.square(self.target_Q - self.Q))
# RMSprop优化器,最小loss函数
self.optimizer = tf.train.RMSPropOptimizer(self.learning_rate).minimize(self.loss)
优先经验回放 Prioritized Experience Replay
理论
优先经验回放(PER)由Tom Schaul于2015年提出 。该idea是,对于训练,某些经验可能比其他经验更重要,但不那么频繁出现。
因为统一对批次进行抽样(随机选择经验),所以这类经验丰富的样本几乎没有机会被选中。
这就是为什么,利用PER,通过使用一个标准来定义每个经验元组的优先级来改变采样分布。
当预测值和TD目标存在很大差异的时,设置优先获得该经验,这也意味模型需要多了解该经验信息。
使用TD误差幅度的绝对值:
将优先级放在每个回放缓冲区的经验中。
但是不能只做贪婪的优先次序,因为这会导致总是训练相同的经验(具有很高的优先级),从而过度拟合。
因此,引入随机优先级的概念,产生被选择中用于回放的概率。
因此,在每个时间步骤中,获得具有此概率分布的一批样本并在其上训练网络模型。
但是,这里仍有问题。请记住,通过正常的体验重放,使用随机更新规则。因此,对体验进行抽样的方式必须与它们的原始分布相匹配。
当有正常的经验时,选择正常分布的经验 - 简单地说,随机选择经验。无偏采用,每个经验都有相同的机会,所以优化器可以正常更新的学习模型的权重。
但是,这种放弃了随机采样使用优先级采样的方式,会向高优先级样本引入偏差(更多机会被选中)。
这种情况下,更新模型权重会有过拟合的风险。与低优先级经验(=偏差)相比,具有高优先级的经验样本可能多次用于训练。因此,模型只会使用一小部分经验更新权重。
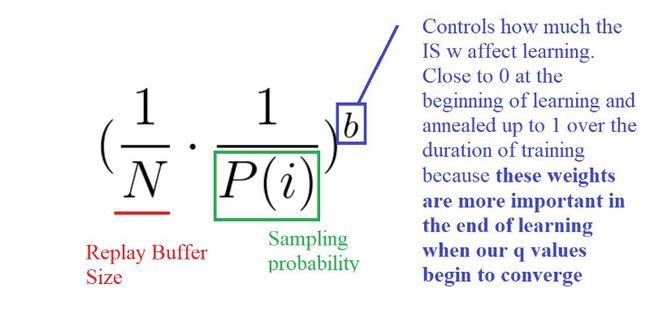
为了纠正这种偏差,可以使用重要度采样(IS),通过减少常见样本的权重来调整更新模型。
对高优先级的样本的权重几乎不进行调整(需要网络将多次看到这些经验),而对低优先级样本的权重进行彻底的更新。
b的作用是控制这些重要性采样权重对学习的影响程度。在实践中,b参数在训练期间逐步上升至1,因为当我们的q值开始收敛时,这些权重在学习的后期更为重要。如文所述,无偏性的更新对误差收敛是至关重要的。
实现
这一次,这个实现有点复杂。
首先,我们不能只根据优先级对所有经验回放样本(Experience Replay Buffers)进行排序来实现优先经验回放PER。对经验样本插入优先级的算法时间复杂度为O(nlogn),采样过程的算法时间复杂对为O(n),因此这个效率并不高。
正如这篇非常好的文章所解释的那样,我们需要使用另一种数据结构而不是排序数组,即 an unsorted sumtree。
SumTree 是二叉树(一种树形结构),每个节点最多只有两个子节点。 每片树叶存储每个样本的优先级p, 每个树枝节点只有两个分叉, 节点的值是两个分叉的合。
这种结构在更新树(更新优先级参数)和采样将非常有效率(O(longn))。
然后,我们创建一个包含sumtree和data的内存对象。
接下来,采样得到大小为k的小批量样本,(代码里)将范围[0,total_priority]划分为k个范围。从每个范围均匀地采样。
最后,从sumtree中检索对应于这些采样值中的每一个的转换(体验)。
当我们深入了解jupyter notebook中的完整细节时,会更加清晰。
Doom Deathmatch 智能体
(Doom Deathmatch =《毁灭战士》死亡竞赛,游戏中多人对战场景)
该智能体是具有PER和固定q目标的Dueling Double Deep Q Learning。
我们制作了一个实现视频教程:jupyter notebook的代码点击这里。
就这样!你刚刚创建了一个学会玩Doom的智能体。真棒!请记住,如果您希望该agent具有非常好的性能,则需要更多GPU时间(大约两天时间的训练)!
通过2-3小时的CPU训练(是CPU),我们的agent理解了他们需要杀死敌人才能继续前进。如果他们向前移动而不杀死敌人,他们将在获得vest之前被杀死。
不要忘记自己实现代码的每个部分。尝试修改我给你的代码非常重要。尝试增加epochs,更改架构architecture,添加固定的Q值fixed Q-values,更改学习率,使用更难的环境......等等。玩得开心!
要记得,这是一篇很重要的文章,所以一定要真正理解为什么我们使用这些新策略,它们如何工作的,以及使用它们的优势。
在下一篇文章中,我们将学习基于数值和基于策略的强化学习算法之间的一种非常棒的混合方法。这是最先进算法的基准:Advantage Actor Critic(A2C)。下节课,你将实现一个学习玩Outrun的智能体!
想要继续查看该篇文章相关链接和参考文献?
长按链接点击打开:
https://ai.yanxishe.com/page/TextTranslation/1081
AI研习社每日更新精彩内容,观看更多精彩内容:
用PyTorch来做物体检测和追踪
用 Python 做机器学习不得不收藏的重要库
初学者怎样使用Keras进行迁移学习
一文带你读懂 WaveNet:谷歌助手的声音合成器
等你来译:
强化学习:通往基于情感的行为系统
如何用Keras来构建LSTM模型,并且调参
高级DQNs:利用深度强化学习玩吃豆人游戏
用于深度强化学习的结构化控制网络 (ICML 论文讲解)