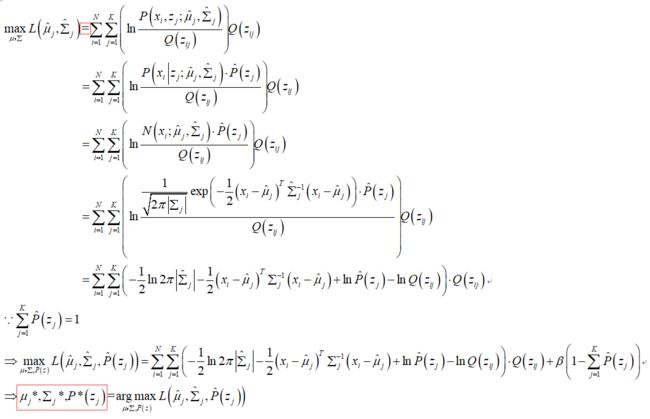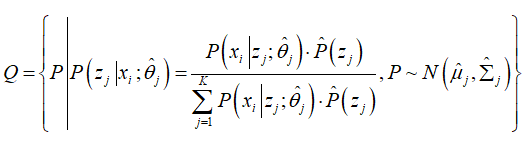返回主页
EM (Expectation Maximization)算法是一种迭代算法,由 Dempster 等人于1977年提出。EM 算法最大的价值在于解决含隐变量的概率模型参数的极大似然估计问题,通过 E步更新后验概率,通过 M步求参数极大似然估计,EM算法常用于无监督学习,如聚类问题。
EM 算法的难点在于要理解目标函数的解并非问题的最终解,这一点与许多经典机器学习算法不同,问题的最终解是隐变量 z 的后验分布 Q 分布,而目标函数的解是参数 theta 和 P 分布,theta 往往用正态分布的参数表示。Q 分布无法通过传统的极大似然估计求解,所以只能先通过目标函数求 theta 和 P,再间接的求出 Q,更新 Q 之后再刷新目标函数更新 theta 和 P,循环往复直至收敛。所以,theta 和 P 就像一组桥梁,连接了目标函数与问题假设。
0、先导知识:Jeson 不等式
1、数据集与特征空间
2、目标函数(极大似然估计)
此刻,如果能使 >= 变为 = ,那么目标函数就明确了,因此继续往下推:
此时,等号得以成立,更新目标函数:
此时,可见目标函数是关于 mu, sigma, P 的函数,P 是每个隐变量所占的权重,因此 P 的和 = 1。下面自然就是求极大似然估计:
3、假设空间
EM 算法的难点在于要理解目标函数的解并非问题的最终解,这一点与许多经典机器学习算法不同,问题的最终解是隐变量 z 的后验分布 Q 分布,而目标函数的解是参数 theta 和 P 分布,theta 往往用正态分布的参数表示。Q 分布无法通过传统的极大似然估计求解,所以只能先通过目标函数求 theta 和 P,再间接的求出 Q,更新 Q 之后再刷新目标函数更新 theta 和 P,循环往复直至收敛。所以,theta 和 P 就像一组桥梁,连接了目标函数与问题假设。
问题的假设可以理解为: Q 分布是关于 theta 和 P 分布的函数,Q* 是问题的最终解,也是假设函数的最优值;theta* 和 P* 是目标函数的最优解,也是假设函数的最优解。
4、优化步骤
4.1、参数初始化(EM 对初始值敏感)
4.2、更新 Q 分布(E步)
4.3、更新 mu, sigma, P(M步)
4.4、循环4.2、4.3,直到误差足够小,算法停止
4.5、得到最终的 Q 分布,取其大者为隐变量最终的类别标记
5、算法收敛性证明
手写 GMM 并与 Sklearn 对比
# -*- coding: utf-8 -*-
import os
import copy
#import random as rd
import numpy as np
import pandas as pd
#from sklearn.utils import shuffle
#from sklearn.model_selection import train_test_split
#from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.mixture import GaussianMixture
from scipy.stats import norm
from sklearn.metrics import silhouette_score
class GMM(object):
def __init__(self, z, tol, max_iter, init_params, verbose):
self.z = z
self.tol = tol
self.max_iter = max_iter
self.init_params = init_params
self.verbose = verbose
def fit(self, x):
'''模型训练'''
# 参数初始化
N, n = x.shape
Q = np.zeros([N, self.z])
pdf = np.ones([N, self.z])
P = np.random.uniform(low=0, high=1, size=(self.z, 1))
if self.init_params == "kmeans":
km = KMeans(n_clusters=self.z, init="k-means++")
km.fit(x)
mu = km.cluster_centers_
elif self.init_params == "random":
mu = np.random.randn(self.z, n) * 0.01
else:
raise ValueError("init_params must be 'kmeans' or 'random'")
std = np.std(x, axis=0)
std = np.tile(std, self.z).reshape(self.z, n)
mu_update = np.zeros_like(mu)
std_update = np.ones_like(std)
err_mu_res = []
err_std_res = []
for epoch in range(self.max_iter):
# E
for j in range(self.z):
# 隐变量外循环
for col in range(n):
# 列内循环,计算联合分布
pdf[:, j] *= norm.pdf(x[:, col], mu[j, col], std[j, col])
Q[:, j] = pdf[:, j] * P[j]
# 计算Q分布
Q = Q / np.sum(Q, axis=1).reshape(-1, 1)
# M
for j in range(self.z):
# 更新每个隐变量的参数值
mu_update[j] = x.T.dot(Q[:, j]) / np.sum(Q[:, j])
std_update[j] = np.sqrt(Q[:, j].dot((x - mu[j])**2) / np.sum(Q[:, j]))
P[j] = np.mean(Q[:, j])
# 停止条件
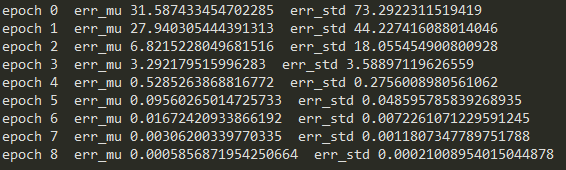
err_mu = np.sum(np.abs(mu - mu_update))
err_std = np.sum(np.abs(std - std_update))
if self.verbose:
print(f"epoch {epoch} err_mu {err_mu} err_std {err_std}")
err_mu_res.append(err_mu)
err_std_res.append(err_std)
if err_mu <= self.tol and err_std <= self.tol:
break
else:
mu = copy.deepcopy(mu_update)
std = copy.deepcopy(std_update)
return Q, P, err_mu_res, err_std_res
def predict(self, Q):
'''判断类别'''
labels = np.argmax(Q, axis=1)
return labels
if __name__ == "__main__":
file_path = os.getcwd()
dataSet = pd.read_csv(file_path + "/swiss.csv")
x = dataSet[["Fertility", "Agriculture", "Catholic", "InfantMortality"]].values
# 手写模型
model = GMM(z=3, tol=0.001, max_iter=1000, init_params="kmeans", verbose=True)
Q, P, err_mu_res, err_std_res = model.fit(x)
labels = model.predict(Q)
score = silhouette_score(x, labels, metric="euclidean")
print(f"手写模型轮廓系数 {score}")
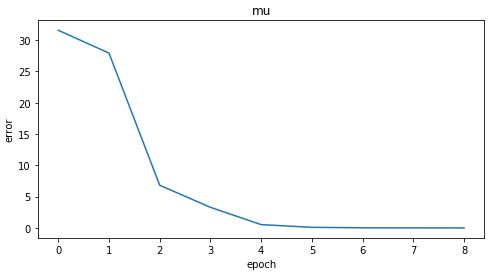
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(err_mu_res)
plt.xlabel("epoch")
plt.ylabel("error")
plt.title("mu")
plt.show()
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(err_std_res)
plt.xlabel("epoch")
plt.ylabel("error")
plt.title("std")
plt.show()
# sklearn
gmm = GaussianMixture(n_components=4, tol=0.001, max_iter=1000, init_params="kmeans")
gmm.fit(x)
gmm.predict_proba(x)
labels = gmm.predict(x)
print(f"sklearn 模型轮廓系数 {score}")
返回主页