算法实验报告—DP
算法实验报告——DP
- 最长公共子序列(LCS)
-
- 题目
- 思路
- 代码
- 运行结果
- 计算矩阵连乘
-
- 题目
-
- 题目分析
- 变量说明
-
- p数组
- dp【i】【j】
- 核心思想分析
- 代码
- 运行结果
- 凸多边形的最优三角划分
-
- 题目
- 最优子结构证明
- 递推关系
- 代码
- 防卫导弹
-
- 题目
- 思路
- 代码
- 石子合并
-
- 题目
- 思路
- 代码
- 运行结果
- 01背包问题
-
- 思路
-
- 其他的dp数组
- 1.dp[ i+1 ][ j ]表示0到i这i+1个物品中重量不超过j的最大价值
- 2.dp[ i ][ j ]表示从0到i-1这i个物品重量不超过j的最大价值
- 3.dp[ i+1 ][ j ]表示从前i个物品中选择:价值为j的最小的w
最长公共子序列(LCS)
题目
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说,若给定序列X=
思路
给定串s和t,求最长公共子序列 数组dp[i][j]:si和tj的公共子序列长度
dp[i+1][j+1] = Math.max(dp[i][j+1],dp[i+1][j],dp[i][j]+1),
如果si+1和tj+1是同一个字符
= Math.max(dp[i][j+1],dp[i+1][j])
如果不是同一个字符
代码
public class Longest_Common_Substring {
String[][] ans;
public String solve(String s,String t){
ans = new String[s.length()+1][t.length()+1];
for(int i=0;i<s.length()+1;i++) {
for (int j = 0; j < t.length()+1; j++) {
ans[i][j] = "";
}
}
// System.out.println(Arrays.deepToString(ans));
for(int i=0;i<s.length();i++){
for(int j=0;j<t.length();j++){
if(s.charAt(i) == t.charAt(j)){
ans[i+1][j+1] = ans[i][j]+s.charAt(i);
}else{
if(ans[i+1][j].length() > ans[i][j+1].length()){
ans[i+1][j+1] = ans[i+1][j];
}else{
ans[i+1][j+1] = ans[i][j+1];
}
}
}
}
return ans[s.length()][t.length()].toString();
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("输入两个串");
String s = reader.readLine();
String t = reader.readLine();
Longest_Common_Substring demo = new Longest_Common_Substring();
System.out.println(s+"和"+t+"的最长组序列为"+demo.solve(s,t));
}
}
运行结果
计算矩阵连乘
题目
计算一系列矩阵相乘所需要的最少步骤数。
题目分析
两个矩阵相乘的必要条件是第一个矩阵的列和第二个矩阵的行相同。假设第一个矩阵是pq,第二个矩阵是qr,那么所需要的计算步骤是pqr次。
因此假设有n个矩阵,只需要n+1个空间就可以表征这些矩阵的性质。为了便于下标处理,矩阵从下标1开始。
变量说明
p数组
记录矩阵的规模,每一个元素对应相应下标矩阵的一维长度,最后一个元素是最后一个剧真的二维长度。
dp【i】【j】
从小标i到j的矩阵相乘的步骤数,因为是求最小值,所以给一个大的初值,矩阵自己不和自己相乘,所以对角线值为0。
核心思想分析
还是有分治的思想。从两个矩阵开始连乘,计算出结果并保存起来,规模扩大到两个,调用之前/查询之前计算出来的结果,取多种可能的最小值,当规模扩大到n的时候,对应下标dp【1】【n】的值就是结果。自底向上体现在从规模小开始,记录结果留给规模大的查看。
每次规模扩大有两种情况:
如果原来的规模不进行划分,直接并上新加入的元素,那么就等于原来规模的结果加上合并的开销。
如果在新的规模上重新进行划分,那么就设立标志k,从k位置切开,两个更小的部分规模小于备忘录的最大规模,是可以查得到的,所以直接查,加上合并的规模。
代码
package Algorithms_算法.实验.动规;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
/**
* @author Xinchen Liu
* @date 2021/5/31 9:25
*/
//a[ai][aj],b[bi][bj]相乘的递推式
public class Multiple_Matrix {
ArrayList<int[][]> matrix_set = new ArrayList<>();
int[][] dp;//dp【i】【j】:从i到j的计算量,同样舍弃 0的那一行那一列
int[][] ans;
int[] p;//矩阵的宽度,第0个元素舍弃,1-size是对应矩阵的一维宽度,最后一位是最后一个矩阵的二维宽度
int j=0;
public int solve(){
p = new int[matrix_set.size()+2];
for(int i=1;i<=matrix_set.size();i++){
p[i] = matrix_set.get(i-1).length;
}//存储第i个矩阵的行数
p[p.length-1] = matrix_set.get(matrix_set.size()-1)[0].length;
//存储最后一个矩阵的列数
System.out.println(Arrays.toString(p));
dp = new int[matrix_set.size()+1][matrix_set.size()+1];
for(int[] tmp:dp){
Arrays.fill(tmp,998);//求最小值,就赋值一个大的数
}
for(int i=1;i<dp.length;i++){
dp[i][i] = 0;//自乘不需要考虑,下表0的舍弃
}
for(int distance = 1;distance < matrix_set.size();distance++){
//连乘范围
for(int i=1;i + distance <= matrix_set.size();i++){
j= i + distance;//连乘区间的右端点
dp[i][j] = Math.min(dp[i][j-1] + p[i]*p[j]*p[j+1],
dp[i+1][j] + p[i+1]*p[i+2]*p[j]);//这边其实没搞懂
//先计算不划分的情况,i到j的区间等于i到j-1的乘上第j个矩阵或者i+1到j的乘上第i个矩阵
//开始划分,i-k一组,k+1-j一组,所以k可以等于i
for(int k=i;k<j;k++){
System.out.println(i+","+j+","+k+".");
int a = dp[i][j];
int b = dp[i][k] + dp[k+1][j] + p[i]*p[k+1]*p[j+1];
System.out.println("当前最小:"+a+";本次划分的大小:"+b);
dp[i][j] = Math.min(a,b);
//i的行数,k和j的列数
}
}
}
for(int[] t:dp){
System.out.println(Arrays.toString(t));
}
return dp[1][matrix_set.size()];//从1到n的连乘次数
}
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
Multiple_Matrix demo = new Multiple_Matrix();
int[][] tmp = new int[100][];
int flag = 0;
String s;
while(true){
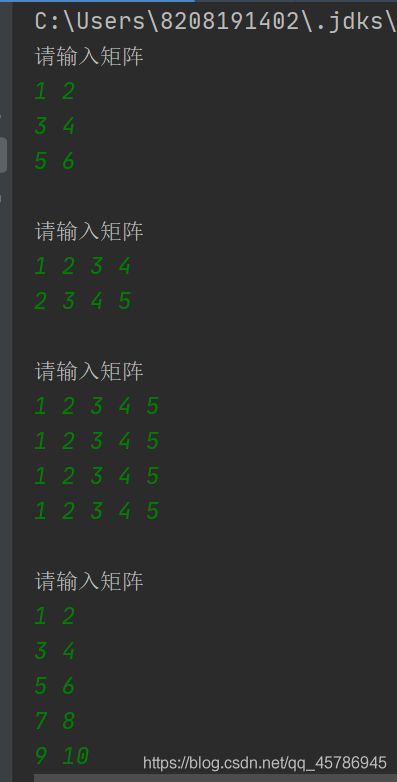
System.out.println("请输入矩阵");
s = reader.readLine();
if(s.equals("-1")){
break;
}
while(true){
s = reader.readLine();
if(s.equals("")){
break;
}
String[] t = s.split(" ");
tmp[flag] = new int[t.length];
for(int i=0;i<t.length;i++){
tmp[flag][i] = Integer.parseInt(t[i]);
}
flag++;
}
int[][] toadd = new int[flag][];
for(int i=0;i< toadd.length;i++){
toadd[i] = tmp[i];
}
demo.matrix_set.add(toadd);
tmp = new int[100][];
flag = 0;
}
// demo.matrix_set.add(new int[][]{
{1,2},{3,4},{5,6}});//3*2
// demo.matrix_set.add(new int[][]{
{1,2,3,4},{2,3,4,5}});//2*4
// demo.matrix_set.add(new int[][]{
{1,2,3,4,5},{1,2,3,4,5},{1,2,3,4,5},{1,2,3,4,5}});//4*5
// demo.matrix_set.add(new int[][]{
{1,2},{3,4},{5,6},{3,4},{5,6}});//5*2
System.out.println(demo.solve());
}
}
for(int i=0;i<dp.length;i++){
dp[i][i] = 0;//自己到自己的距离为0
}
不考虑矩阵自乘,也就是区间长度为0表示没有矩阵 要相乘。
for(int distance = 1;distance < points.size();distance++)
从两个矩阵相乘,跨度为1开始。
j= i + distance;//连乘区间的右端点
dp[i][j] = Math.min(dp[i][j-1] + p[i]*p[j]*p[j+1],
dp[i+1][j] + p[i+1]*p[i+2]*p[j])
先计算不重新划分的情况,也就是采纳前一个规模的划分,加上和现在矩阵相乘的开销。i到j的区间等于i到j-1的乘上第j个矩阵或者i+1到j的乘上第i个矩阵的最小值。
//开始划分,i-k一组,k+1-j一组,所以k可以等于i
for(int k=i;k<j;k++){
System.out.println(i+","+j+","+k+".");
int a = dp[i][j];
int b = dp[i][k] + dp[k+1][j] + p[i]*p[k+1]*p[j+1];
System.out.println("当前最小:"+a+";本次划分的大小:"+b);
dp[i][j] = Math.min(a,b);
//i的行数,k和j的列数
从i到j,也就是划分当前规模,划分之后的规模一定小于当前规模,这些规模的结果都已经算出来了,只需要直接从备忘录取出,加上合并的开销,就得到这种划分的解,选取最小的。
return dp[1][matrix_set.size()];
当区间宽度覆盖所有矩阵时结束。
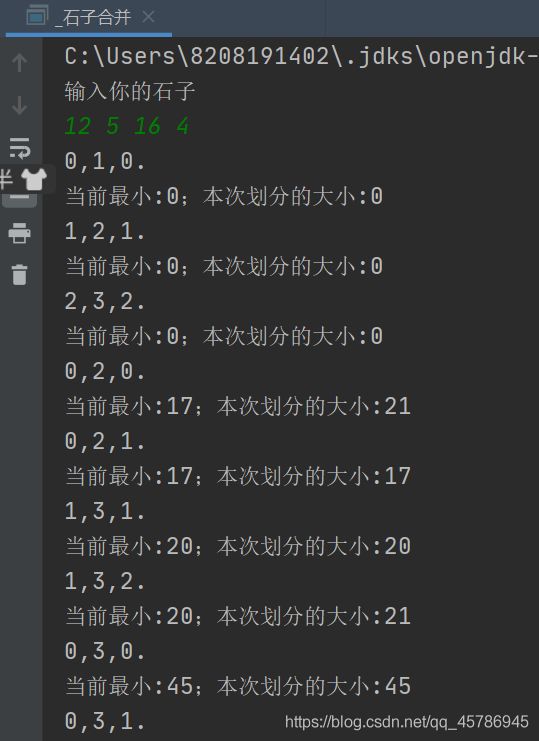
运行结果
凸多边形的最优三角划分
题目
(1)凸多边形的三角剖分:将凸多边形分割成互不相交的三角形的弦的集合T。
(2)最优剖分:给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得该三角剖分中诸三角形上权之和为最小。
最优子结构证明
证:T确定的这两个子多边形的三角剖分也是最优的。
因为若有{V0,V1……Vk}和{V0,V1……Vk}更小权的三角剖分,而当前的最小权划分是从前一个最小权划分得到的,如果存在,就和前一个规模的最小权划分矛盾,将导致T不是最优三角剖分。因此,凸多边形的三角剖分问题具有最优子结构性质。
递推关系
设t [ i ][ j ] ,1 <= i < j<= n为凸多边形{V i - 1 ,V i……V j}的最优三角剖分所对应的权值函数值 / 最优值。
那么新的最优剖分的权值包含:三角形V i - 1V kV j的权 + 子多边形{V i - 1,V i……V k}的权 + 子多边形{V k,V k + 1……V j}的权
凸多边形最优三角剖分满足动态规划的最优子结构性质,可以从自底向上逐渐推出整体的最优。
(1)确定合适的数据结构
采用二维数组weight[ ][ ]记录各个顶点之间的连接权值,二维数组t[ ][ ]存放各个子问题的最优值,二维数组s[ ][ ]存放各个子问题的最优策略。
(2)初始化输入顶点数n,然后依次输入各个顶点之间的连接权值存储在二维数组weight[ ][ ]中,令n=n-1(顶点标号从v0开始),t [ i ][ i ]=0,s[ i ][ i ]=0,其中i=1,2,3,4……,n-1。
(3)循环(自底向上 + 备忘录)(从三个顶点开始算)
按照递归关系式计算3个顶点{vi - 1,vi,vi + 1}的最优三角剖分,j=i+1,将最优值存入t [ i ][ i ],同时将最优策略存入s[ i ][ i ],i=1,2,3,……,n-1。
按照递归关系式计算4个顶点{v i-1,vi,vi+1,vi+2}的最优三角剖分,j=i+2,将最优值存入t [ i ][ i ],同时将最优策略存入s[ i ][ i ],i=1,2,3,……,n-2。
以此类推,直到求出所有顶点{v0,v1,v2,……,vn}的最优三角剖分,并将最优值存入t [ 1 ][ n ],将最优策略记入s[ 1 ][ n ]
(4)构造最优解
根据最优决策信息数组s[ ][ ]递归构造最优解,即输出凸多边形的最优剖分的所有弦。s[ 1 ][ n ] 表示凸多边形最优三角剖分位置,即最优化分的顶点坐标。
对于给定的一组顶点组成的凸多边形,选择最优化分位置s[ 1 ][ n ],把多边形分成两个子多边形{ v0,v1,v2,……,Vs[1][n] } 和 { Vs[1][n] ,v1,v2,……,vn}。
如果子问题1为空,即没有一个顶点,说明V0Vs[1][n]是一条边,不是弦,不需要输出,否则,输出该弦:V0<----->V(s[1][n])
如果子问题2为空,即没有一个顶点,说明Vs[1][n]Vn是一条边,不是弦,不需要输出,否则,输出该弦V(s[1][n])<----->Vn
递归构造两个子问题{ v0,v1,v2,……,Vs[1][n] } 和 { Vs[1][n] ,v1,v2,……,vn
},一直递归到子问题为空停止。
代码
public class Triangulation {
double[][] dp;
ArrayList<int[]> points = new ArrayList<>();
public double solve(){
dp = new double[points.size()+1][points.size()+1];
for(int i=0;i<dp.length;i++){
dp[i][i] = 0;//自己到自己的距离为0
}
for(int i=0;i<points.size();i++){
dp[i][i+1] = distance(points.get(i), points.get(i + 1));
}
int j = 0;
for(int distance = 2;distance < points.size();distance++){
for(int i=1;i + distance <= points.size();i++){
j= i + distance;
dp[i][j] = Math.min(dp[i][j-1] + distance(points.get(j), points.get(j+1))
+distance(points.get(i), points.get(j))+
distance(points.get(i), points.get(j-1)),
dp[i+1][j] + distance(points.get(i), points.get(i+1))
+distance(points.get(i), points.get(j))+
distance(points.get(i+1), points.get(j)));
//开始划分,i-k一组,k+1-j一组,所以k可以等于i
for(int k=i;k<j;k++){
System.out.println(i+","+j+","+k+".");
double a = dp[i][j];
double b = dp[i][k] + dp[k+1][j] + distance(points.get(k), points.get(k+1))
+distance(points.get(i), points.get(k+1))+
distance(points.get(j), points.get(k+1));
System.out.println("当前最小:"+a+";本次划分的大小:"+b);
dp[i][j] = Math.min(a,b);
}
}
}
return dp[1][points.size()];
}
public double distance(int[] a,int[] b){
return Math.pow(Math.pow(a[1]-b[1],2)+Math.pow(a[0]-b[0],2),0.5);
}
for(int i=0;i<dp.length;i++){
dp[i][i] = 0;//自己到自己的距离为0
}
初始化,到自身没有边,也就是权值为0
for(int distance = 2;distance < points.size();distance++)
三角形至少要三个点,因此跨度从2开始。
j= i + distance;//连乘区间的右端点
dp[i][j] = Math.min(dp[i][j-1] + distance(points.get(j), points.get(j+1))
+distance(points.get(i), points.get(j))+
distance(points.get(i), points.get(j-1)),
dp[i+1][j] + distance(points.get(i), points.get(i+1))
+distance(points.get(i), points.get(j))+
distance(points.get(i+1), points.get(j)));
先计算不划分的情况,即采用之前一个规模的划分结果,加上和当前点连接的开销
//开始划分,i-k一组,k+1-j一组,所以k可以等于i
for(int k=i;k<j;k++){
System.out.println(i+","+j+","+k+".");
double a = dp[i][j];
double b = dp[i][k] + dp[k+1][j] + distance(points.get(k), points.get(k+1))
+distance(points.get(i), points.get(k+1))+
distance(points.get(j), points.get(k+1));
System.out.println("当前最小:"+a+";本次划分的大小:"+b);
dp[i][j] = Math.min(a,b);
从i到j,也就是多边形的顶点之间遍历选取一个划分点,划分之后的规模一定小于当前规模,这些规模的结果都已经算出来了,只需要直接从备忘录取出,加上合并的开销,就得到这种划分的解,选取最小的。
return dp[1][points.size()];
当区间宽度覆盖所有顶点时结束。
防卫导弹
题目
一种新型的防卫导弹可截击多个攻击导弹。它可以向前飞行,也可以用很快的速度向下飞行,可以毫无损伤地截击进攻导弹,但不可以向后或向上飞行。但有一个缺点,尽管它发射时可以达到任意高度,但它只能截击比它上次截击导弹时所处高度低或者高度相同的导弹。现对这种新型防卫导弹进行测试,在每一次测试中,发射一系列的测试导弹(这些导弹发射的间隔时间固定,飞行速度相同),该防卫导弹所能获得的信息包括各进攻导弹的高度,以及它们发射次序。现要求编一程序,求在每次测试中,该防卫导弹最多能截击的进攻导弹数量,一个导弹能被截击应满足下列两个条件之一:
a)它是该次测试中第一个被防卫导弹截击的导弹;
b)它是在上一次被截击导弹的发射后发射,且高度不大于上一次被截击导弹的高度的导弹。
思路
求出在我后面发射的,高度比我小的导弹数目,的最大值。
代码
public class Cruise_Missile {
int[][] message;//时间,高度
int[] dp;
public Cruise_Missile(int[][] message){
this.message = message;
dp = new int[message.length];
}
public int solve(){
Arrays.sort(message, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0] < o2[0] ? -1:1;
}
});
for(int i= message.length-1;i>=0;i--){
for(int j=i;j< message.length;j++){
if(message[j][1] < message[i][1]){
dp[i] = Math.max(dp[i],dp[j]+1);
}
}
}
return dp[0];
}
}
石子合并
题目
在一个圆形操场的四周摆放着n堆石子(n<= 100),现要将石子有次序地合并成一堆。规定每次只能选取相邻的两堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。编一程序,由文件读入堆栈数n及每堆栈的石子数(<=20)。
选择一种合并石子的方案,使得做n-1次合并,得分的总和最小;
思路
和前几题非常相似,自底向上,任选相邻的两堆合并,记录合并开销,然后逐渐扩大规模,每次扩大在采纳前一规模划分和不采纳前一规模,重新划分中选取最小的,同时计算合并开销。
代码
public class _石子合并 {
int[] costs;
int[][] dp;
int j;
public _石子合并(int[] costs){
this.costs = costs;
this.dp = new int[costs.length][costs.length];
for(int[] tmp:dp){
Arrays.fill(tmp,998);//求最小值,就赋值一个大的数
}
for(int i=0;i<dp.length;i++){
dp[i][i] = 0;//自乘不需要考虑,下表0的舍弃
}
}
public int solve(){
for(int div=1;div < costs.length;div++){
for(int i=0;i + div < costs.length;i++){
j = i+div;
dp[i][j] = Math.min(dp[i][j-1] ,dp[i+1][j] );
for(int k=i;k<j;k++){
System.out.println(i+","+j+","+k+".");
dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k+1][j]);
System.out.println("当前最小:"+dp[i][j]+";本次划分的大小:"+(dp[i][k]+dp[k+1][j]));
}
dp[i][j]+=sum(i,j);
}
}
for(int[] t:dp){
System.out.println(Arrays.toString(t));
}
return dp[0][costs.length-1];
}
public int sum(int a,int b){
int sum = 0;
for(int i=a;i<=b;i++){
sum+=costs[i];
}
return sum;
}
public static void main(String[] args) {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("输入你的石子");
String stones = reader.readLine();
String[] stone = stones.split(" ");
int[] data = new int[stone.length];
for(int i=0;i<stone.length;i++){
data[i] = Integer.parseInt(stone[i]);
}
_石子合并 demo = new _石子合并(data);
int ans = demo.solve();
System.out.println(ans);
}
}
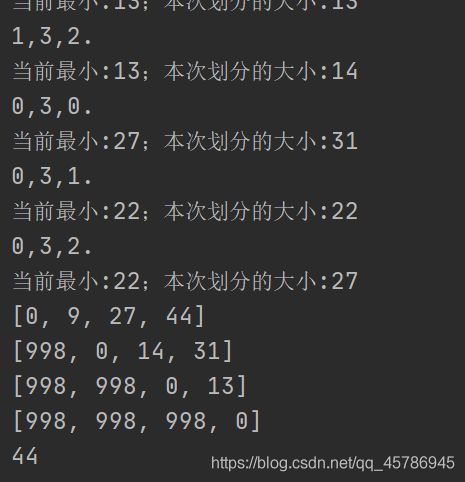
运行结果
01背包问题
思路
有多种思路,也就是不同意义的dp数组。
(1)最基础的,递归,不用dp。
public int recursion(int i,int j){
int res;
if(w[i] > W){
res = recursion(i+1,j);//选不了该物品
}else if(i == n){
res = 0;//物品遍历完了
}else{
res = Math.max(recursion(i+1,j),recursion(i+1,j-w[i])+v[i]);
// 不选第i个 选第i个
}
return res;
}
和斐波那契一样有很多重复计算,每次状态转移都是从第i个向第i+1个转变,
(2)如果能存下第i+1次计算的结果,就不用了在后面的状态再计算前一个状态的值了。
public int recursion(int i,int j){
if(dp[i][j] > 0){
return dp[i][j];
}//如果是之前算过的状态,就直接用。
int res;
if(w[i] > W){
res = recursion(i+1,j);//选不了该物品
}else if(i == n){
res = 0;//物品遍历完了
}else{
res = Math.max(recursion(i+1,j),recursion(i+1,j-w[i])+v[i]);
// 不选第i个 选第i个
}
return dp[i][j] = res;//保存数值
}
dp = new int[n+1][W+1];
Arrays.fill(dp,-1);
int ans1 = recursion(0,W);
System.out.println(ans1);
(3)减少递归对系统栈的消耗,把dp的定义和使用带入循环
dp[n][j] = 0;
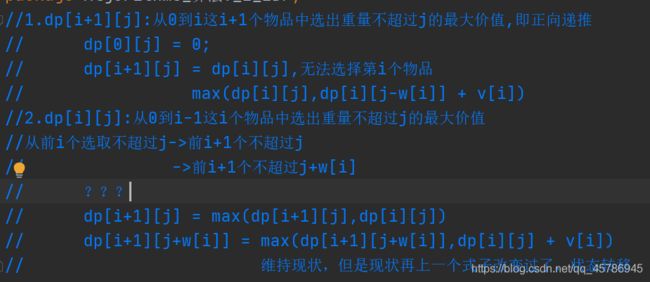
dp[i][j] = dp[i+1][j],无法选择第i个物品
max(dp[i+1][j],dp[i+1][j-w[i]] + v[i])
for(int i = n-1;i>=0;i--){
for(int j=0;j<=W;j++){
if(j<w[i]){
dp[i][j] = dp[i+1][j];
}else{
dp[i][j] = Math.max(dp[i+1][j],dp[i+1][j-w[i]] + w[i]);
}
}
}
return dp[0][W];
(4)再进一步,能不能用一位数组暂存结果,节约空间,因为每一次计算都只与前一个状态有关,不同于多边形的三角划分,子问题规模可变,背包问题子问题划分规模是固定的,不会涉及到一次以前的状态。
public int solve_01(){
for(int i = 0;i<n;i++){
for(int j = W;j>=0;j--){
dp[j] = Math.max(dp[j],dp[j - w[i]]+v[i]);
}
}
return dp[W];
}
public int solve_full(){
for(int i = 0;i < n;i++){
for(int j = w[i];j<=W;j++){
dp[j] = Math.max(dp[j],dp[j - w[i]]+v[i]);
}
}
return dp[W];
}
其他的dp数组
1.dp[ i+1 ][ j ]表示0到i这i+1个物品中重量不超过j的最大价值
public int solve1(){
for(int i=0;i<n;i++){
for(int j=0;j<=W;j++){
if(j<w[i]){
dp[i+1][j] = dp[i][j];
}else{
dp[i+1][j] = Math.max(dp[i][j],dp[i][j-w[i]] + v[i]);
}
}
}
return dp[n][W];
}
//对于j从0取到w的原因
//因为你不知道上一次选了之后,还剩下多少重量可选,所以要把每种可能的重量都遍历一遍
2.dp[ i ][ j ]表示从0到i-1这i个物品重量不超过j的最大价值
public int solve2(){
for(int i=0;i<n;i++){
for(int j=0;j<=W;j++){
dp[i+1][j] = Math.max(dp[i+1][j],dp[i][j]);
if(j + w[i] < W){
dp[i+1][j+w[i]] = Math.max(dp[i+1][j+w[i]],dp[i][j] + v[i]);
}
}
}
return dp[n][W];
}
3.dp[ i+1 ][ j ]表示从前i个物品中选择:价值为j的最小的w
这种解法适合于重量的大小远小于价值的大小时,如果用原来的方法会超时
int[][] dp = new int[n+1][(n+1)*(m+1)];
public int solve(){
Arrays.fill(dp,99999999);
for(int i=0;i<n;i++){
for(int j=0;j<(n+1) * (m+1);j++){
if(j < v[i]){
dp[i+1][j] = dp[i][j];
}else{
dp[i+1][j] = Math.min(dp[i][j],dp[i][j - v[i]] + w[i]);
}
}
}
int ans = 0;
for(int i=0;i<=(n+1)*(m+1);i++){
if(dp[n][i] <= W){
ans = i;
}
}
return ans;
}