本文主要参考Andrew Ng老师的Machine Learning公开课，并用《机器学习实战》中的源码实现。

Logistic Regression基本原理

Logistic分布

Logistic Distribution的分布函数和密度函数如下：

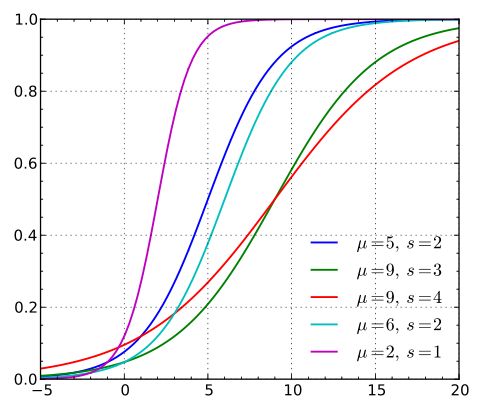
上式中是位置参数，是形状参数。下图是不同参数对logistic分布的影响，从图中可以看到可以看到影响的是中心对称点的位置，越小中心点附近增长的速度越快。而常常在深度学习中用到的非线性变换函数是逻辑斯蒂分布的的特殊形式。

image.png

二项Logistic Regression模型

image.png

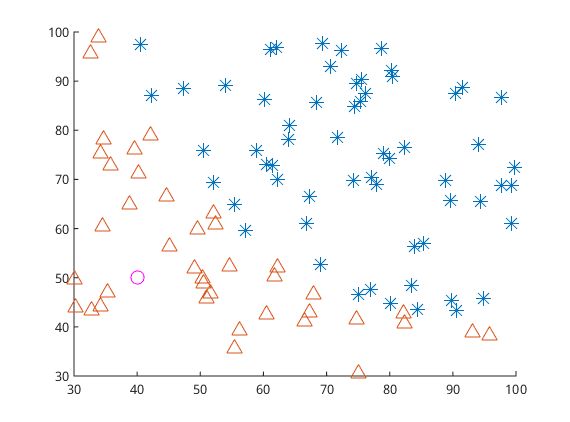
逻辑回归是为了解决分类问题，根据一些已知的训练集训练好模型，再对新的数据进行预测属于哪个类。对于上图中的数据，逻辑回归的目标是找到一个有足够好区分度的决策边界，从而能够将两类很好的分开。

分离边界的维数与空间的维数相关。如果是二维平面，分离边界就是一条线（一维）。如果是三维空间，分离边界就是一个空间中的面（二维）。如果是一维直线，分离边界就是直线上的某一点。

假设输入的特征向量为，取值为。对于二维的空间，决策边界可以表示为，假如存在一个例子使得，那么可以判断它类别为，这个过程实际上是感知机，即只通过决策函数的符号来判断属于哪一类。而逻辑回归需要再进一步，它要找到分类概率与输入向量的直接关系，然后通过比较概率值来判断类别，而刚好上文中的logistic function能满足这样的要求，它令决策函数的输出值，求解这个式子得到了输入向量下导致产生两类的概率为：

其中称为权重，称为偏置，其中的看成对的线性函数，有时候为了书写方便，会将写入，即，并取。然后对比上面两个概率值，概率值大的就是对应的类。

又已知一个事件发生的几率odds是指该事件发生与不发生的概率比值，二分类情况下即。取odds的对数就是上面提到的logistic function，。从而可以得到一种对逻辑回归的定义，输出的对数几率是由输入的线性函数表示的模型，即逻辑斯蒂回归模型(李航.《统计机器学习》)。另一种对逻辑回归的定义，线性函数的值越接近正无穷，概率值就越接近1；线性值越接近负无穷，概率值越接近0，这样的模型是逻辑斯蒂回归模型(李航.《统计机器学习》)。因此逻辑回归的思路是，先拟合决策边界(这里的决策边界不局限于线性，还可以是多项式)，再建立这个边界与分类的概率联系，从而得到了二分类情况下的概率。

有了上面的分类概率，就可以建立似然函数，通过极大似然估计法来确定模型的参数。设，似然函数为，对数似然函数为

优化方法

优化的主要目标是找到一个方向，参数朝这个方向移动之后使得似然函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是

$\begin{eqnarray} min J(w) &=& \min \frac{1}{m} \sum_{j=1}^{m}Cost(h_w(x^{(i)}),y^{(i)}) \\\\ &=& \min {-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}\log h_w(x^{(i)})+(1-y^{(i)})\log(1-h_w(x^{(i)}))]} \end{eqnarray}$

梯度下降法

最大似然估计就是要求得使取最大值时的，但因此处的添加了一个负号，所以必须用梯度下降法求解最佳参数。但若此处的没有添加负号，则需要用梯度上升法求解最佳参数。

先把对的一阶偏导求出来，且用表示。是梯度向量。

$\begin{eqnarray} g_j &=& \frac{\partial J(w)}{\partial w_j}\\\\ &=& -\frac{1}{m}\sum_{i=1}^{m}(\frac{y^{(i)}}{h_w(x^{(i)})} h_w(x^{(i)}) (1-h_w(x^{(i)}))(-x_{j}^{(i)}) + (1-y^{(i)})\frac {1}{1-h_w(x^{(i)})}h_w(x^{(i)})(1-h_w(x^{(i)}))x_j^{(i)}) \\\\ &=& -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}-h_w(x^{(i)}))x_{j}^{(i)}) \end{eqnarray}$

梯度下降是通过对的一阶导数来找下降方向（负梯度），并且以迭代的方式来更新参数，更新方式为

为迭代次数。每次更新参数后，可以通过比较或者与某个阈值大小的方式来停止迭代，即比阈值小就停止。

如果采用梯度上升法来推到参数的更新方式，会发现计算公式完全一样，所以采用梯度上升发和梯度下降法是一样的。

随机梯度下降法

从上面梯度下降法中的公式中可以看到，每次更新回归系数时都需要遍历整个数据集，如果有数十亿样本和成千上万个特征，则梯度下降法的计算复杂度就太高了。随机梯度下降法一次仅用一个样本点来更新回归系数：

梯度下降过程向量化

约定训练数据的矩阵形式如下，的每一行为一条训练样本，而每一列为不同的特称取值：

$\begin{equation} x= \left[ \begin{matrix} x^{(1)}\\\\ x^{(2)}\\\\ \ldots\\\\ x^{(m)} \end{matrix} \right] = \left[ \begin{matrix} x_0^{(1)} & x_1^{(1)} & \ldots & x_n^{(1)}\\\\ x_0^{(2)} & x_1^{(2)} & \ldots & x_n^{(2)}\\\\ \ldots & \ldots & \ldots & \ldots \\\\ x_0^{(m)} & x_1^{(m)} & \ldots & x_n^{(m)} \end{matrix} \right] , y= \left[ \begin{matrix} y^{(1)}\\\\ y^{(2)}\\\\ \ldots\\\\ y^{(m)} \end{matrix} \right] \end{equation}$

约定待求的参数θ的矩阵形式为：

先求并记为：

$\begin{equation} A=x \cdot \theta = \left[ \begin{matrix} x_0^{(1)} & x_1^{(1)} & \ldots & x_n^{(1)}\\\\ x_0^{(2)} & x_1^{(2)} & \ldots & x_n^{(2)}\\\\ \ldots & \ldots & \ldots & \ldots \\\\ x_0^{(m)} & x_1^{(m)} & \ldots & x_n^{(m)} \end{matrix} \right] \cdot \left[ \begin{matrix} \theta_0\\\\ \theta_1\\\\ \ldots\\\\ \theta_n \end{matrix} \right] = \left[ \begin{matrix} \theta_0x_0^{(1)} + \theta_1x_1^{(1)} + \ldots + \theta_nx_n^{(1)}\\\\ \theta_0x_0^{(2)} + \theta_1x_1^{(2)} + \ldots + \theta_nx_n^{(2)}\\\\ \ldots \\\\ \theta_0x_0^{(m)} + \theta_1x_1^{(m)} + \ldots + \theta_nx_n^{(m)} \end{matrix} \right] \end{equation}$

求并记为：

$\begin{equation} E=h_\theta(x)-y= \left[ \begin{matrix} g(A^{(1)})-y^{(1)}\\\\ g(A^{(2)})-y^{(2)}\\\\ \ldots \\\\ g(A^{(m)})-y^{(m)} \end{matrix} \right] = \left[ \begin{matrix} e^{(1)}\\\\ e^{(2)}\\\\ \ldots\\\\ e^{(m)} \end{matrix} \right] =g(A)-y \end{equation}$

由上式可知可以由一次计算求得。

再有：

综合上面的式子有：

正则化

由于模型的参数个数一般是由人为指定和调节的，所以正则化常常是用来限制模型参数值不要过大，也被称为惩罚项。一般是在目标函数(经验风险)中加上一个正则化项即

而这个正则化项一般会采用L1范数或者L2范数。其形式分别为和。

首先针对L1范数，当采用梯度下降方式来优化目标函数时，对目标函数进行求导，正则化项导致的梯度变化当是取1，当时取-1.

从而导致的参数减去了学习率与公式的乘积，因此当的时候，会减去一个正数，导致减小，而当的时候，会减去一个负数，导致又变大，因此这个正则项会导致参数取值趋近于0，也就是为什么L1正则能够使权重稀疏，这样参数值就受到控制会趋近于0。L1正则还被称为 Lasso regularization。

然后针对L2范数，同样对它求导，得到梯度变化为(一般会用来把这个系数2给消掉)。同样的更新之后使得的值不会变得特别大。在机器学习中也将L2正则称为weight decay，在回归问题中，关于L2正则的回归还被称为Ridge Regression岭回归。weight decay还有一个好处，它使得目标函数变为凸函数，梯度下降法和L-BFGS都能收敛到全局最优解。

需要注意的是，L1正则化会导致参数值变为0，但是L2却只会使得参数值减小，这是因为L1的导数是固定的，参数值每次的改变量是固定的，而L2会由于自己变小改变量也变小。而公式中的也有着很重要的作用，它在权衡拟合能力和泛化能力对整个模型的影响，越大，对参数值惩罚越大，泛化能力越好。

《机器学习实战》代码

梯度上升法：

def gradAscent(dataMatIn, classLabels):
    """梯度上升法"""
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m, n = shape(dataMatrix)
    alpha = 0.1
    maxCycles = 500
    weights = ones((n, 1))
    for k in range(maxCycles):
        a = dataMatrix * weights
        h = sigmoid(dataMatrix * weights)  # 100*3 3*1
        error = (labelMat - h)
        weights = weights + alpha / m * dataMatrix.transpose() * error
    return weights

随机梯度下降法：

def stocGradAscent0(dataMatrix, classLabels):
    """随机梯度上升法，但是迭代次数不够，且可能存在局部波动现象"""
    m, n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i] * weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights


def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    """改进的随机梯度上升法"""
    m, n = dataMatrix.shape
    weights = ones(n)
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4 / (1.0 + j + i) + 0.01 # alpha在每次迭代时都进行了调整
            randIndex = int(random.uniform(0, len(dataIndex))) # 随机选取样本数据
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del (dataIndex[randIndex])
    return weights

参考文献

【机器学习笔记1】Logistic回归总结
【机器学习算法系列之二】浅析Logistic Regression
牛顿法与拟牛顿法学习笔记（一）牛顿法

Logistic Regression