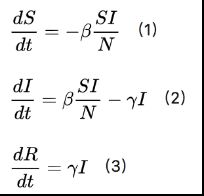备注:此文仅在有限信息的基础上,对当下的疫情提供数学建模思路。博主非相关医学、传染学等专业研究者,因此对模型的适用性和准确性不加以保证。但是本模型在参数辨识、建模方法以及数据分析方法等方面有一定借鉴作用。欢迎小伙伴来一起交流和探讨。另,本文禁止转载。
ps:实际完成时间为2020年2月6日,因此在时间上有一定的滞后性。
----------分割线
截止至2月6日,根据官方公布的确诊人数情况,实际上除了湖北地区疫情发展较为严重外,其他省份的疫情已经处在可控状态中。一方面毕竟非感染源省份,另一方面也是因为地区医疗条件能够满足供应,同时在防疫措施方面较为严格、落实到位。所以在当下的疫情态势下,全社会都在聚焦现在到底有没有控制住态势、疫情未来将怎样发展,而最终什么时候能正式复工。当下的全社会隔离的措施下,每个人的生活都受到了严重影响(尤其是不喜欢做饭又没法出门吃饭和点外卖的本人)。因此,本文将以四川地区的感染情况为例,预测未来的疫情发展,并对正式复工的时间进行探讨。
一、基本数据
1.1 武汉迁入四川总人数
四川于1月21日公布第一例确诊案例,考虑到疫情潜伏期的影响(平均为10天),因此假定四川第一例案例为1月11日受到来自武汉的肺炎患者感染。
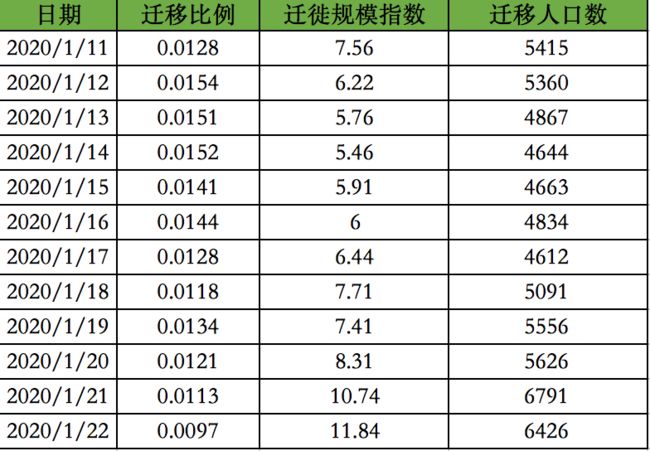
根据百度迁移指数(http://qianxi.baidu.com/?from=groupmessage),以武汉在1月11日~1月22日总计迁出500万人口为基数进行计算,得到由武汉迁入四川的分日人数:
2.2 武汉外来人员中感染者比例
SIR模型(简单介绍,更多模型理论可参见相关文献研究):
人口总量可分类为易感人群s(t)、感染人群i(t)、隔离态人群r(t)(治愈或死亡)。
四川境内的感染源为外来武汉的感染者,以及之后受到感染后的四川境内人员。因此初始的感染源为武汉外来人员。由SIR模型可知,在前期疫情未受到重视时,感染者以基本传染数R0(R0=β/γ)进行自然传播,同时考虑在N远大于I的情况下,S≈N,因此在自然情况下:
即感染者的人数占总人数的比例每日等比例上升,在已知β和γ的情况下可以求取。因此假定1月11日武汉人口的感染者比例为α,可以计算每日由武汉人口迁移注入的感染者数量。
二、基本模型参数确定
SIR模型中,需要确定的参数包括β、γ和α。γ可以直接采用1/10(根据官方公布的数据显示,初期的潜伏期一般为2-7天,最长为14天,平均为10天)。因此实际需要确定的参数为β和α,其中β可以转化为β=R0*γ。根据目前的研究结果,新冠肺炎R0大于SARS的R0,估计处在3-7之间,因此可以做出一些假定。当R0=5,α=0.002时,四川境内1月11日~1月21日的感染情况为:
为了确定准确的参数,我们需要与官方公布的确诊人数做对比。然而实际上确诊人数在时间周期上具有延迟性和隐瞒性,基于10天的平均潜伏期,我们将四川省公布的确诊人数倒推10天看一下存量感染者和确诊人数的对比曲线:
可以看到,基本走向是符合的,但是模型的存量感染者数目大于确诊人数。因此,如何确定确定R0和α呢?这里考虑利用以“确诊人数倒推10天/存量感染者的比例的标准差”为最小化目标函数,求取R0和α,即认为在前期疫情尚未爆发,群众尚未引起重视时,只有部分比例的存量感染者会主动就医并确诊,这个比例在分日的情况下应该是较为接近的,因此标准差应当较小。
同时需要满足参数约束:
- 3≤R0≤7;
- α≤0.002,即原始武汉总人口1000万人情况下,初始感染人数不会超过2W人;
- 2月1日的确诊总人数(倒推十天为1月22日)/1月22日的存量感染者总人数比例不小于50%,即截止2月1日,群众对疫情情况已经引起足够重视,至少有不少于50%的感染者会主动就医。
利用以上优化条件,可以求得最佳参数为:
R0=4.4,α=0.0011
由此可得存量感染者和确诊人数曲线为:
三、R0值的变化
初期的R0=4.4的确足以引起高度重视,根据R0自然传染数的定义,是指在前期没有额外的防疫干预措施的情况下,平均每个病人能传染的人数。根据传播动力学:
R0=kbD
其中k是一个有传染能力的患者平均每天与易感人群的接触次数,b是每次接触传染成功的概率,D是可以传播的时间,可以认为等同于潜伏周期。
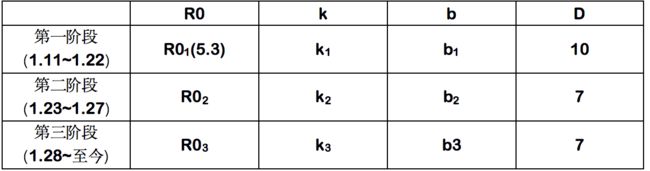
基于实施情况考虑将疫情发展分为三个阶段:
第一阶段:1月11日~1月22,疫情自然发展,此时R0为基本传染数的基准值;
第二阶段:1月23日~1月23日,由武汉封城逐渐引起公众重视,此时疫情进入新发展阶段。根据官方公布数据,由于感染者积极就诊,加强预防和锻炼等方式,D由原始的平均10天潜伏期下降为7天;同时公众开始进行自我隔离和互相隔离使得k值稳定下降,以及采用勤洗手、戴口罩等方式使得b值稳定下降;
第三阶段:1月28日至今,由政府主导,积极采取宣传措施和隔离措施,使得k值和b值下降到最低值,在不发生爆发性病毒感染事件的情况下,此时R0进入最新的稳定最低值。
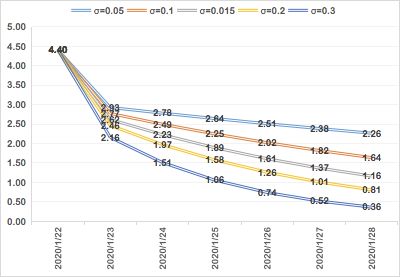
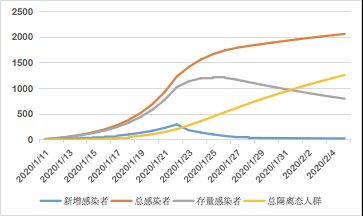
因此,当第二阶段的R0每日按照σ等比例下降时,至1月28的R0情况如下图所示:
例如,当σ=0.3时,四川省的感染者情况为:
可以看到,经过1月23日之后的积极调控后,每日新增感染者数量开始减少,最终R03<1,此时每日新增隔离态人群数(治愈或死亡)会超过每日新增感染者,随着时间推移,最终疫情会逐渐消失。
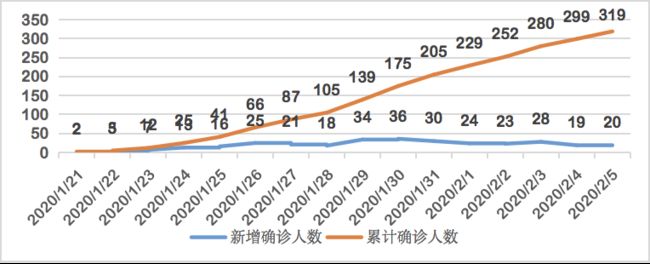
那么怎么确定现阶段的R03呢?我们可以从四川省发布的确诊案例数据上面来进行初步观察:
根据官方公布的数据,1月21日 1月30日之间每日新增确诊人数是不断增长趋势的,而1月31日开始,每日新增确诊人数开始呈下降趋势,开始稳定在每日2025人之间。早起的确诊人数是有较长的时间滞后性的,一是群众未引起足够重视,因此存在感染后未正确就医的情况,二是早起检测手段不足,从检测到确诊需要更长的时间,在前文中我们也是假设早期的确诊人员实际上10天前便已感染;后期的确诊人数滞后性逐渐减小,主要是由于各个小区和街道社区在排查力度下不断增强,以及核酸检测可以快速出现结果,因此后期的确诊人员的被感染时间应当地域10天。这里假定第二阶段及第三阶段的确诊时间滞后性缩短为7天,而实际上1月23日之后7天即为1月30日,1月30日的新增确诊人数达到顶峰,而相对应的时间节点证号为1月23日群众对疫情引起重视,积极采用多种隔离方式使得疫情进一步得到抑制,这也表明文中的假设是具有合理性的。进一步,我们便可以利用第二阶段和第三阶段的每日新增感染者和确诊患者的人数数量来做确定σ值以及现在的R0值,优化目标修正为“每日新增人数倒推7天/新增感染者的比例的标准差”为最小化目标函数来求解。
可以求解得到最新的结果:
σ=0.14,R03=1.27
显然上述求解结果并不精确,但是求取到的R03=1.35可以作为一个参考值,而当前的实际R03应当处在该基准值的一定区间范围内,这里考虑实际R03处在基准值的±30%的区间范围内。则可以分为三种情况进行讨论:
- 悲观假设:R03=1.27+30%*1.27=1.65;
- 中性假设:R03=1.27;
- 乐观假设:R03=1.27-30%*1.27=0.89;
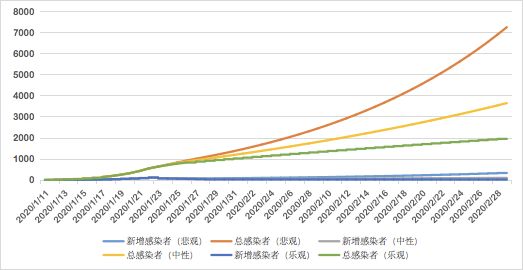
三种不同情况下的数据对比情况如下图所示:
四、疫情预测
在求取到现阶段R0值后,我们便可以对疫情发展进行预测,并根据情况制定下一步控制措施。理论上讲,如果某一病毒基本传染数R0大于1,在不加防控的情况下它会传染几乎所有人群,而三种不同的假设中,只有乐观假设的R0值低于1,因此把握好现在的疫情动态并加强疫情控制显得尤为重要。下面针对三种情况进行具体分析。
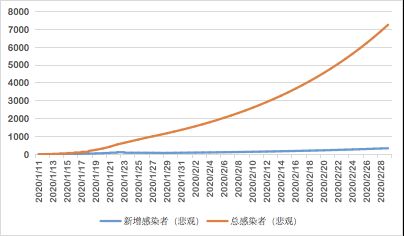
4.1 悲观假设
在悲观假设情况下,之后的每日新增感染者和存量感染者将持续增加,感染者数量并不会出现拐点。截至2月底,将有累计感染者7526人和存量感染者3165人,实际上疫情已经失控。此时防疫工作还需要不断加大,重点包括三方面:
- 严格进行感染者隔离,并利用各种宣传渠道和管控渠道减少民众出行和聚会,从而让k值下降;
- 监督群众外出必须佩戴口罩,同时对各类场所进行定期消毒,从而让b值下降;
- 做好群众的宣传工作,提高群众警惕性,督促轻微症状的患者会及时就医,或提供社区医生定期上门检测,从而让传染期D进一步下降;
4.2 中性假设
在中性假设情况下,实际上1月23日起日新增感染者有下降的趋势,迎来第一个拐点,但是由于后期的R0=1.27>1,因此无法真正抑制住疫情,最终日新增感染者又逐渐增多。截至2月底,将有累计感染者3654人和存量感染者1230人。具体观察一下日新增人数的曲线:
可以看到在1月23日之后一定程度上已经抑制了疫情发展,但随着后期存量感染人数的增加,日新增感染者会逐渐上升。实际上第三阶段的R0=1.27较初始的R0=4.4已经下降了71.1%,这说明前期的控制措施已经取得了很好的效果,而接下来需要做的,就是进一步做好感染者隔离、场所消毒等防疫工作。实际上,随着疫情时间阵线上的拉长,群众对疫情的重视程度是会逐渐上升的,因此k、b值都会逐渐降低,同时国家医学力量推动感染周期D值进一步下降。因此R0并不会保持长期不变,而应当是随着当下控制措施和医学力量的增强而逐渐降低,并且完全可能由1.33降低至1以下。
4.3 乐观假设
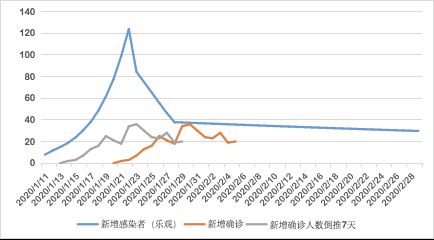
在乐观假设情况下,自1月23日起日新增感染者人数将不断下降,同时随着隔离态人群的增加,总的存量感染者将逐渐减少并消失,此时疫情完全被消灭。截至2月底,将有累计感染者1987日和存量感染者460人,此时日新增感染者人数已经少于50人。我们看一下新增感染人数和官方公布新增确诊人数曲线:
可以看到,乐观假设下的新增感染者数目增长趋势与新增确诊人数倒推7天的趋势是比较一致的。为什么是趋势一致,而不是数目一致,主要是因为部分感染者在潜伏期内不会爆发出明显症状,这也是我们需要对接触过感染者的人群进行医学隔离的目的。同时,也是考虑到部分患者受到感染后能够自行治愈从而不会就医并确诊,以及部分患者瞒报以及官方数据不够准确等原因。因此,官方公布的确诊人数实际并不表示真正的感染者数量。而基于两者趋势上的一直,我们其实也可以判断目前四川区域的整体防控情况处在乐观状态。如果接下来的确诊人数与乐观假设下的新增感染者人数趋势上一致,则可以进一步和模型实现双向确认,即确认当前四川省的防控情况处在乐观状态,当前R0<1。
五、什么时候复工?
复工问题应当是当下国家、社会以及所有企业和个人都密切关注的问题。而目前国家尚未复工的原因主要还是考虑到存在很多尚未监测到的潜伏期感染者,若直接复工,将会造成新的一轮感染。考虑到模型中的乐观假设与目前实际情况较为接近,下面我们就以乐观情况下讨论什么时候适宜复工的问题。
在乐观假设情况下,至2月底,将有累计感染者1987日和存量感染者460人,同时每日会有日新增感染者人数约30人。显然,尽管此时已经控制住了疫情,但是每日30人新增感染者明显不满足复工需求,即R0值需要进一步下降。如前文中已经提到,随着疫情时间阵线上的拉长,R0应当是随着时间逐渐降低的。参考非典期间,早期非典的R0值在3以上之间,而到了非典后期,严格的防疫措施使得SARS的基本传染数下降到0.4。因此,理论上,通过严格防疫措施,R0值是可以再降低的。目前最有针对性的措施就是将感染者进行严格隔离。
在最理想的情况下,如果从今天开始,所有感染者进行自我隔离,那么感染者将不会有途径感染他人,那么在7天传染期过后,将不会再有存量感染者,这也是专家目前的呼吁所在。结合R0=kbD的公式可以知道,将患者进行隔离,实际是降低患者平均每天与易感人群的接触次数k值。考虑一下几种情况:
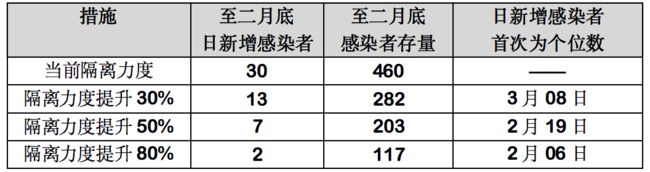
考虑从2月5日起,隔离力度有不同的提升,此时的感染曲线和感染情况为:
可以看出,若隔离力度提升50%,至二月底的日新增感染数为7人,若隔离力度提升80%,则至二月底的日新增感染数为1人,此时基本上已经完全控制住疫情,具备复工条件。实际上,现在各省份的隔离措施都在不断增强,具体体现在:
- 小区出入及超市等公共场所已经限制必须测量体温及佩戴口罩后才能出入;
- 各公共场所已经做好定期消毒措施;
- 社区政府人员主动上门进行隔离宣传并检查人员隔离情况;
- 互联网技术支撑,让群众可以利用APP或小程序等监测到当地区域、周边小区的人员确诊情况等,从而引起足够重视并减少出门机会。
所以隔离力度提升50%~80%完全是可行的并且符合实际情况的。考虑在隔离力度提升50%的情况下,2月19日首次实现日新增感染者不高于10人,经过7天的潜伏期后,2月26日,医学诊断上的新增人数将首次降至个位数,此时疫情已经在掌控之中。若能积极隔离好感染者存量人群,经过严格的14天隔离,预计于3月11日便可实现正式复工。