Introduction to Deep Neural Networks
Introduction to Deep Neural Networks
Neural networks are a set of algorithms, modeled loosely after the human brain, that are designed to recognize patterns. They interpret sensory data through a kind of machine perception, labeling or clustering raw input. The patterns they recognize are numerical, contained in vectors, to which all real-world data, be it images, sound, text or time series, must be translated.
Neural networks cluster and classify. You can think of them as a clustering and classification layer on top of data you store and manage. They group unlabeled data according by similarities among the example inputs, and they classify data when they have a labeled training set to work with.
As you think about one problem deep learning can solve, ask yourself: What categories do I care about? What can I act on? Those are labels: spam or not spam, good guy or bad guy, angry customer or happy customer. Then ask: Do I have data to accompany those labels?
For example, if you want to identify a group of people at risk for cancer, your training set would be a list of cancer patients along with all the data associated to their unique IDs, which could include everything from explicit features like age and smoking habits to raw data such as time series that track their motion, or logs of their behavior online, which likely indicate a great deal about lifestyle, habits and interests.
Searching for potential dating partners, future major-league superstars, a company’s most promising employees, or potential bad actors, involves much the same process of contructing a training set by amassing vital stats, social graphs, raw text communications, click streams, etc.
Neural Network Elements
Deep learning is a name for a certain set of stacked neural networks composed of several node layers. A node is a place where computation happens, loosely patterned on the human neuron and firing when sufficient stimuli pass through. It combines input from the data with a set of coefficients, or weights, that either amplify or mute that input. These input-weight products are summed and the sum is passed through a node’s so-called activation function.
Here’s a diagram of what one node might look like.
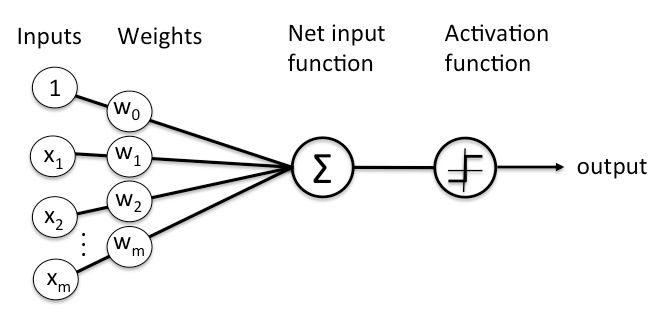
A node layer is a row of those neuronlike switches that turn on or off as the input is fed through the net. Each layer’s output is simultaneously the subsequent layer’s input, starting from an initial input layer receiving your data.
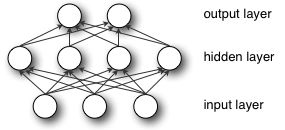
Pairing adjustable weights with input features is how we assign significance to those features with regard to how the network classifies and clusters input.
Key Concepts of Deep Neural Networks
Deep-learning networks are distinguished from the more commonplace single-hidden-layer neural networks by their depth; that is, the number of node layers through which data passes in a multistep process of pattern recognition.
Traditional machine learning relies on shallow nets, composed of one input and one output layer, and at most one hidden layer in between. More than three layers (including input and output) qualifies as “deep” learning.
In deep-learning networks, each layer of nodes is trains on a distinct set of features based on the previous layer’s output. The further you advance into the neural net, the more complex the features your nodes can recognize, since they aggregate and recombine features from the previous layer.
This is known as feature hierarchy, and it is a hierarchy of increasing complexity and abstraction. It makes deep-learning networks capable of handling very large, high-dimensional data sets with billions of parameters passing through nonlinear functions.
Above all, these nets are capable of discovering latent structures withinunlabeled, unstructured data, which is the vast majority of data in the world. Another word for unstructured data is simply raw media; i.e. pictures, texts, video and audio recordings. Therefore, one of the problems deep learning solves best is in processing and clustering the world’s raw, unlabeled media, discerning similarities and anomalies in data that no human has organized in a relational database or put a name to.
For example, deep learning can take a million images, and cluster them according to their similarities: cats in one corner, ice breakers in another, and in a third all the photos of your grandmother. This is the basis of so-called smart photo albums.
Now apply that same idea to other data types: Deep learning might cluster raw text such as emails or news articles. Emails full of angry complaints might cluster in one corner of the vector space, while satisfied customers, or spambot messages, might cluster in others. This is the basis of various messaging filters, and can be used in customer-relationship management (CRM). The same applies to voice messages.
With time series, data might cluster around normal/healthy behavior and anomalous/dangerous behavior. If the time series data is being generated by a smart phone, it will provide insight into users’ health and habits; if it is being generated by an autopart, it might be used to prevent catastrophic breakdowns.
Deep-learning networks perform automatic feature extraction without human intervention, unlike most traditional machine-learning algorithms. Given that feature extraction is a task that can take teams of data scientists years to accomplish, deep learning is a way to circumvent the chokepoint of limited experts. It augments the powers of small data science teams, which by their nature do not scale.
When training on unlabeled data, each node layer in a deep network learns features automatically by repeatedly trying to reconstruct the input from which it draws its samples, attempting to minimize the difference between the network’s guesses and the probability distribution of the input data itself. Restricted Boltzmann machines, for examples, create so-called reconstructions in this manner.
In the process, these networks learn to recognize correlations between certain relevant features and optimal results – they draw connections between feature signals and what those features represent, whether it be a full reconstruction, or with labeled data.
A deep-learning network trained on labeled data can then be applied to unstructured data, giving it access to much more input than machine-learning nets. This is a recipe for higher performance: the more data a net can train on, the more accurate it is likely to be. (Bad algorithms trained on lots of data can outperform good algorithms trained on very little.) Deep learning’s ability to process and learn from huge quantities of unlabeled data give it a distinct advantage over previous algorithms.
Deep-learning networks end in an output layer: a logistic, or softmax, classifier that assigns a likelihood to a particular outcome or label. We call that predictive, but it is predictive in a broad sense. Given raw data in the form of an image, a deep-learning network may decide, for example, that the input data is 90 percent likely to represent a person.
Example: Feedforward Networks
Our goal in using a neural net is to arrive at the point of least error as fast as possible. We are running a race. The starting line for the race is the state in which our weights are initialized, and the finish line is the state of those parameters when they are capable of producing accurate classifications and predictions.
The race itself involves many steps, and each of those steps resembles the others. Just like a runner, we will engage in a repetitive act over and over to arrive at the finish. Each step for a neural network involves a slight update in its weights, an incremental adjustment to their quantities.
A collection of weights, whether they are in their start or end state, is also called a model, because it is an attempt to model data’s relationship to ground-truth labels, to grasp its structure. Models normally start out bad and end up less bad, changing over time as the neural network updates its parameters.
This is because a neural network is born in ignorance. It does not know which weights and biases will translate the input best to make the correct guesses. It has to start out with a guess, and then try to make better guesses sequentially as it learns from its mistakes. (You can think of a neural network as a miniature enactment of the scientific method, testing hypotheses and trying again – only it is the scientific method with a blindfold on.)
Here is a simple explanation of what happens when a neural network learns (more precisely, we’ll discuss a feedforward neural net, the simplest architecture to explain.)
Input enters the network. The coefficients, or weights, map that input to a set of guesses the network makes at the end.
input * weight = guess
Weighted input results in a guess about what that input is. The neural then takes its guess and compares it to a ground-truth about the data, effectively asking an expert “Did I get this right?”
ground truth - guess = error
The difference between the network’s guess and the ground truth is its error. The network measures that error, and walks the error back over its model, adjusting weights to the extent that they contributed to the error.
error * weight's contribution to error = adjustment
The three pseudo-mathematical formulas above account for the three key functions of neural networks: scoring input, calculating loss and applying an update to the model – to begin the three-step process over again. A neural network is a corrective feedback loop, rewarding weights that support its correct guesses, and punishing weights that lead it to err.
The name for one commonly used optimization function that adjusts weights according to the error they caused is called “gradient descent.”
Gradient is another word for slope, and slope, in its typical form on an x-y graph, represents how two variables relate to each other: rise over run, the change in money over the change in time, etc. In this particular case, the slope we care about describes the relationship between the network’s error and a single weight; i.e. that is, how does the error vary as the weight is adjusted.
To put a finer point on it, which weight will produce the least error? Which one correctly represents the signals contained in the input data, and translates them to a correct classification? Which one can hear “nose” in an input image, and know that should be labeled as a face and not a frying pan?
As a neural network learns, it slowly adjusts many weights so that they can map signal to meaning correctly. The relationship between network Error and each of those weights is a derivative, dE/dw, that measures the degree to which a slight change in a weight causes a slight change in the error.
Each weight is just one factor in a deep network that involves many transforms; the signal of the weight passes through activations and sums over several layers, so we use the chain rule of calculus to march back through the networks activations and outputs and finally arrive at the weight in question, and its relationship to overall error.
The chain rule in calculus states that
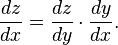
In a feedforward network, the relationship between the net’s error and a single weight will look something like this:

That is, given two variables, Error and weight, that are mediated by a third variable, activation, through which the weight is passed, you can calculate how a change in weight affects a change in Error by first calculating how a change inactivation affects a change in Error, and how a change in weight affects a change in activation.
The essence of learning in deep learning is nothing more than that: adjusting a model’s weights in response to the error it produces, until you can’t reduce the error any more.
Logistic Regression
On a deep neural network of many layers, the final layer has a particular role. When dealing with labeled input, the output layer classifies each example, applying the most likely label. Each node on the output layer represents one label, and that node turns on or off according to the strength of the signal it receives from the previous layer’s input and parameters.
Each output node produces two possible outcomes, the binary output values 0 or 1, because an input variable either deserves a label or it does not. After all, there is no such thing as a little pregnant.
While neural networks working with labeled data produce binary output, the input they receive is often continuous. That is, the signals that the network receives as input will span a range of values and include any number of metrics, depending on the problem it seeks to solve.
For example, a recommendation engine has to make a binary decision about whether to serve an ad or not. But the input it bases its decision on could include how much a customer has spent on Amazon in the last week, or how often that customer visits the site.
So the output layer has to condense signals such as $67.59 spent on diapers, and 15 visits to a website, into a range between 0 and 1; i.e. a probability that a given input should be labeled or not.
The mechanism we use to convert continuous signals into binary output is called logistic regression. The name is unfortunate, since logistic regression is used for classification rather than regression in the linear sense that most people are familiar with. It calculates the probability that a set of inputs match the label.
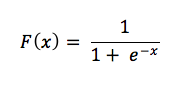
Let’s examine this little formula.
For continuous inputs to be expressed as probabilities, they must output positive results, since there is no such thing as a negative probability. That’s why you see input as the exponent of e in the denominator – because exponents force our results to be greater than zero. Now consider the relationship of e’s exponent to the fraction 1/1. One, as we know, is the ceiling of a probability, beyond which our results can’t go without being absurd. (We’re 120% sure of that.)
As the input x that triggers a label grows, the expression e to the x shrinks toward zero, leaving us with the fraction 1/1, or 100%, which means we approach (without ever quite reaching) absolute certainty that the label applies. Input that correlates negatively with your output will have its value flipped by the negative sign on e’s exponent, and as that negative signal grows, the quantity e to the xbecomes larger, pushing the entire fraction ever closer to zero.
With this layer, we can set a threshold above which an example is labeled 1, and below which it is not. You can set different thresholds as you prefer – a low threshold will increase the number of false positives, and a high one will increase the number of false negatives – depending on which side you would like to err.
Neural Networks & Artificial Intelligence
In some circles, neural networks are thought of as “brute force” AI, because they start with a blank slate and hammer their way through to an accurate model. They are effective, but to some eyes inefficient in their approach to modeling, which can’t make assumptions about functional dependencies between output and input. That said, gradient descent is not recombining every weight with every other to find the best match – it’s method of pathfinding shrinks the relevant weight space therefore the number of updates by many orders of magnitude.
Introductory Resources
For people just getting started with deep learning, the following tutorials and videos provide an easy entrance to the fundamental ideas of feedforward networks: