开始填坑。太多坑没填以致可以从容选择先填哪个,然而也忘了坑长什么样、怎么填。不过还是希望该填的坑能尽量于月底前填完,毕竟拖到新的一年感觉也不好。
先填之前用 D3.js 复现 Wendy Shijia 的 「Escher's Gallery/埃舍尔画廊」 可视化作品的复盘文章的坑。
网页演示:https://desertsx.github.io/dataviz-in-action/02-eschers-gallery/index.htm
开源代码(可点 Star 支持):DesertsX/dataviz-in-action
在Wendy Shijia 的「 Escher's Gallery」可视化作品复现系列文章(一)里,古柳写到自己想起 CSS Tricks 上的 「Use and Reuse Everything in SVG… Even Animations!」 这篇文章,里面实现了单个立方体/cube,并且使用 标签复用立方体进行堆叠,“他山之石,可以攻玉”,于是想到可以用于「 Escher's Gallery」复现中。
简单看下代码实现思路:在 defs 标签里通过3个宽高21*24的rect/长方形的transform/变形拼出一个 cube,这一步是定义图形,实际图形不会显示在 svg 中;
然后使用 use 标签通过 xlink:href="#cube" 指定上一步定义的 cube,此时只需改变x/y坐标,调用27次就能拼出一个 3*3*3 的大立方体。
值得注意的是:每一层x/y坐标变化是有规律的,x以21的倍数移动,y以12的倍数移动,而每层之间y坐标相差24,均和长方形宽高相关,可见布局很简单。
当然如果你眼尖的话,或许会注意到上面每个 rect 的 transform 参数都不同,skewY/scale/rotate/translate 之间似乎没啥关系,到底怎么拼到一起的,看起来有点玄学,但暂且先这么模仿着实现出来再说。
首先本次用的不再是简单的长方形,而是缺了1/4的正方形,即多边形,直接用 polygon 标签给定6个顶点坐标即可绘制出来,边长暂定36,由最终图表成图效果决定是否进行调整。
同理,画出另外两个多边形,不断调试transform的参数,拼到一起组成一个cube即可(其实调起来还是蛮繁琐的,稍后介绍更优雅的实现方式),当然这里每个多边形unit都有各自id,实际也是对应埃舍尔的每件作品,所以最小元素是一个unit而不是一个cube,且unit顺序依次为上、左、右。
拼出cube后,就可以把这段代码放defs标签里,当然填充的颜色需要去掉,颜色在use使用时由绑定的作品数据类别来指定。
至此,最基本的元素定义完成了,接下来就是结合数据,通过 D3.js 来生成所有 use 标签,并传入相应的x/y坐标以及对应颜色,从而绘制出整个可视化作品即可。
不过古柳一开始完全就是对照着这张图一路复现出来的,手头没有数据集,还需自行爬取。”虽说巧妇难为无米之炊“,但在此之前,古柳想先构造伪数据把布局搞定,实现出整体效果再说,免得万一连布局都搞不定,白花时间去爬数据。
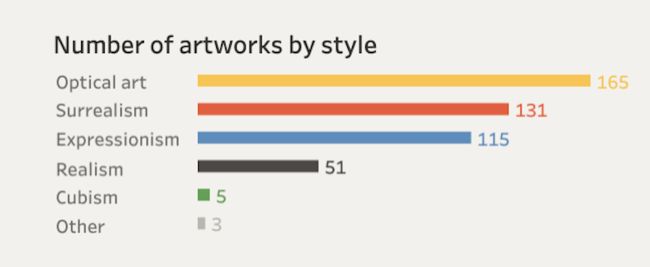
伪数据构造也很简单,470件作品就是470条数据,每件作品只取类型颜色,按照各自数量生成每种颜色,并打乱顺序即可。
const colorScale = {
'yellow': '#ffc533',
'red': '#f25c3b',
'blue': '#5991c2',
'black': '#55514e',
'green': '#5aa459',
'grey': '#bdb7b7',
};
const piecesColor = d3.range(470).map(d => {
if (d < 165) return '#ffc533';
else if (d < 296) return '#f25c3b';
else if (d < 411) return '#5991c2';
else if (d < 462) return '#55514e';
else if (d < 467) return '#5aa459';
else return "#bdb7b7"
});
d3.shuffle(piecesColor);
console.log(piecesColor);
数据有了,就到了最核心的问题,该如何布局了?而布局无非就是要确定每个cube、每个unit的x/y坐标,为了简化问题,这里按照列和行来表示,如左上角的cube为第一列第一行,以(1, 1)表示,依次从上到下,从左到右排列......因而需要知道每条数据的行列位置,比如图中箭头所指向的cube的列数和行数分别应该如何计算?
其实本质就是找规律、理清背后的计算公式,是个有点难度,但并不复杂的数学问题,感兴趣的可以先不看后面内容,自己尝试下解决,出错的过程没准也能看到很有趣的图形。
首先,很明显所有数据按照年龄被分成了7组;而每组内的cube的列数与行数是不仅取决于前几组的行列数,而且与其在本组内的顺序有关。下面简单每个年龄组的unit个数,当然更好的方式是基于数据本身来计算每组年龄的作品数,这里偷懒仍直接人工数下。
分成7个年龄组;一列最多8个cube共24个unit
1898-1917 = 14
1918-1927 = 28 * 3 + 1 = 85
1928-1937 = 7 * 8 * 3 + 6 = 174
1938-1947 = 62
1948-1957 = 27 * 3 = 81
1958-1972 = 14 * 3 - 1 = 41
Year Unknown = 13
以1938-1947这组为例,idx为piecesColor的索引值,即数据的顺序,取值范围为0-469。前面3组共有273个unit(14+85+174=273)、有13列,对于这组内的unit,均需要减去前几组的数量后再计算组内行列数:由于每列有24个unit,因而组内列数只需除24取整再加1即可,parseInt((idx-273)/24)+1,而组内行数则需除24取余数,再考虑到cube要除3再加1即可,parseInt((idx-273)%24/3)。
if (idx < 335) {
group = 4;
col = 13 + parseInt((idx - 273) / 24) + 1;
row = parseInt((idx - 273) % 24 / 3) + 1;
}
由此写出完整的获取行列数的函数即可。
const getXY = (idx) => {
let group;
let groupIdx;
let col;
let row;
if (idx < 14) {
group = 1;
col = 1;
row = parseInt(idx % 24 / 3) + 1;
groupIdx = idx;
}
else if (idx < 99) {
group = 2;
groupIdx = idx - 14;
col = 1 + parseInt(groupIdx / 24) + 1;
row = parseInt(groupIdx % 24 / 3) + 1;
}
else if (idx < 273) {
group = 3;
groupIdx = idx - 99;
col = 5 + parseInt(groupIdx / 24) + 1;
row = parseInt(groupIdx % 24 / 3) + 1;
}
else if (idx < 335) {
group = 4;
groupIdx = idx - 273;
col = 13 + parseInt(groupIdx / 24) + 1;
row = parseInt(groupIdx % 24 / 3) + 1;
}
else if (idx < 416) {
group = 5;
groupIdx = idx - 335;
col = 16 + parseInt(groupIdx / 24) + 1;
row = parseInt(groupIdx % 24 / 3) + 1;
}
else if (idx < 457) {
group = 6;
groupIdx = idx - 416;
col = 20 + parseInt(groupIdx / 24) + 1;
row = parseInt(groupIdx % 24 / 3) + 1;
}
else {
group = 7;
groupIdx = idx - 457;
col = 22 + parseInt(groupIdx / 24) + 1;
row = parseInt(groupIdx % 24 / 3) + 1;
}
return [col, row];
};
接着用 D3.js 生成所有 use 标签即可。注意每列高度隔行相等,以及指定unit的xlink:href时先直接简单用总索引值除3取余数(其实应该用组内索引值groupIdx除3取余数),所以每组最后的cube可能略有问题。
// svg#chart
const svg = d3.select('#chart').append('g');
const cubeWidth = 36; // 40
svg.selectAll('use')
.data(piecesColor)
.join('use')
.attr('xlink:href', (d, i) => i % 3 === 0 ? '#unit-0' : i % 3 === 1 ? '#unit-1' : '#unit-2')
.attr('fill', (d) => d)
.attr('x', (d, i) => getXY(i)[0] * 1.5 * cubeWidth - 80)
.attr('y', (d, i) => 110 + getXY(i)[1] * 1.5 * cubeWidth + (getXY(i)[0] % 2 === 0 ? 0 : 0.75 * cubeWidth));
不过上述步骤主要目的是用伪数据大致理清计算公式、跑通整个布局,所以略有瑕疵可以不用太在意。
截至目前,本次复现的难点其实都解决的差不多了,接下去无非就是爬取数据、替换掉伪数据,然后不断将效果优化到和 Wendy 原始 Tabelau 版本相似即可,这些就留到下一篇文章再讲好了。
最后再回过头把上面不太优雅的cube实现改的优雅些。
其实古柳在复现完,和原作比对时(下图为原作,上图为自己复现的)才突然意识到自己的 cube 图形比较扁,而 Wendy 作品里每个 cube 中间的3条白线是差不多一样长的,也就是说3个 unit 是相同大小的,完全可以用一个旋转出另外两个,只不过当时优化了太久,实在不想回过头再去修改就暂不改进了。
在Wendy Shijia 的「 Escher's Gallery」可视化作品复现系列文章(一) - 20201029一文发布后,也将新的实现思路和 Wendy 交流了下。
在「盘点这个月可视化的那些事 - 20201128」一文里,古柳也提到11月17号晚上看到 Wendy 13号晚上的分享 VizConnect - Drawing Polygons in Tableau: The processing of making Escher's Gallary 录播已经传到油管,于是看了下 Escher's Gallary 作品背后创作过程以及 Wendy 如何绘制的多边形,也确认了下实现方式和古柳所想大致相同。
链接:https://www.youtube.com/watch?v=5AqLHDtGtBg
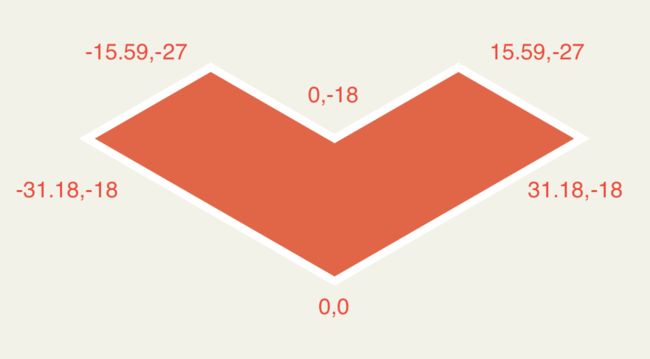
一个unit由两个不完整的正三角形排成,根据简单的数学计算,可以得出所有顶点的坐标,然后用 polygon 画出一个unit,再分别转动-120/120度就可以拼出一个cube。
将a=36,b=18*Math.sqrt(3)取两位小数带入即可(需平移到画布合适位置,方便查看)。
这样更为优雅的unit/cube就绘制出来了!
以上就是本文内容,如果大家还想看到更多干货,欢迎【点赞】、【评论】、【分享】,多多捧场,古柳也有持续创作的动力,毕竟这惨淡的阅读量实在也是有点说服不了自己太频繁更新,还真不是因为懒。逃。