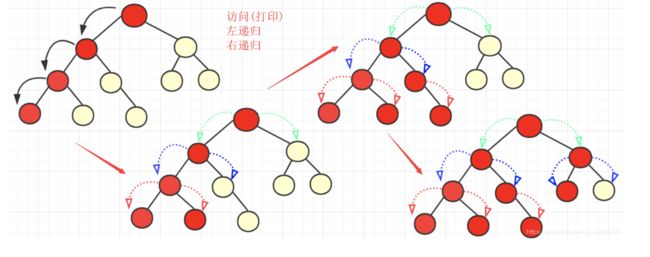
二叉树的遍历方式有3种,分别是前序遍历、中序遍历和后序遍历。这三种方式是以访问父节点的顺序来进行命名的。
假设根节点是N,左节点是L,右节点是R,那么对应的访问遍历顺序如下:
- 前序遍历 N->L->R(根节点 ---> 左节点 ---> 右节点)
- 中序遍历 L->N->R(左节点 ---> 根结点 ---> 右节点)
- 后序遍历 L->R->N(左节点 ---> 右节点 ---> 根节点)
前序遍历规则就是先访问父节点,然后递归左节点(每个节点都要满足前序遍历的规则。比如从根先访问左节点,到了左节点这儿左节点又变成一颗子树,也要满足前序遍历要求。所以就要先访问左节点的左节点,直到没有左节点才会停止),再递归右节点。
访问次序大致为:
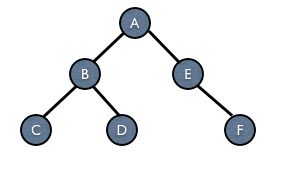
所以,对于以下这棵树,三种遍历方式的结果是
- 前序遍历 ABCDEF
- 中序遍历 CBDAEF
- 后序遍历 CDBFEA
并且可以总结得出以下几个特点:
- 对于前序遍历,第一个肯定是根节点;
- 对于后序遍历,最后一个肯定是根节点;
- 利用前序或后序遍历,确定根节点,在中序遍历中,根节点的两边就可以分出左子树和右子树;
- 对左子树和右子树分别做前面3点的分析和拆分,相当于做递归,我们就可以重建出完整的二叉树;
我们以一个例子做一下这个过程,假设:
前序遍历的顺序是: CABGHEDF
中序遍历的顺序是: GHBACDEF
第一步,我们根据特性A,可以得知根节点是C,然后,根据特性C,我们知道左子树是:GHBA,右子树是:DEF。
C
/ \
GHBA DEF
第二步,取出左子树,左子树的前序遍历是:ABGH,中序遍历是:GHBA,根据特性A和C,得出左子树的父节点是A,并且A没有右子树。
C
/ \
A DEF
/
GBH
第三步,使用同样的方法,前序是BGH,中序是GHB,得出父节点是B,GH是左子树,没有右子树。
C
/ \
A DEF
/
B
/
GH
第四步,前序是GH, 中序是GH, 所以 G是父节点, H是右子树, 没有左子树.
C
/ \
A DEF
/
B
/
G
\
H
第四步,回到右子树,它的前序是EDF,中序是DEF,依然根据特性A和C,得出父节点是E,左右节点是D和F。
C
/ \
A E
/ / \
B D F
/
G
\
H
到此,我们得到了这棵完整的二叉树,因此,它的后序遍历就是 : HGBADFEC
参考链接:https://www.cnblogs.com/xiaokang01/p/9806971.html