凸优化基础理论体系-----计算几何、平面、超平面、凸集、凸函数、凸规划的定义及学习

凸优化基础是人工智能中学习规划的一个重要方式；凸优化性质好，并且即使是日常生活中的许多非凸优化问题，目前最有效的办法也只能是利用凸优化的思路去近似求解。一些例子有：带整数变量的优化问题，松弛之后变成凸优化问题等。
本次博客，林君学长将带大家了解凸优化理论体系，其中理论知识偏多，但林君学长会有一定的辅助题目举例学习，

接下来，就和林君学长一起走进凸优化基础理论体系的世界吧！

一、计算几何定义及学习

1、计算几何的定义

计算几何对几何外形信息的计算机表示、分析和综合。这里的几何外形信息是指那些用来确定某些几何外形的离散数据点或特征多边形。按照给定的信息，建立一定的数学模型，再通过计算机进行计算，求得其他所需的信息，这就是计算机表示。之后还需对所建立的数学模型特性及误差等进行分析、综合，以便逼真地反映出几何形体

2、计算几何是研究什么的？

1）、计算几何的研究对象
计算几何研究的对象是几何图形。早期人们对于图像的研究一般都是先建立坐标系，把图形转换成函数，然后用插值和逼近的数学方法，特别是用样条函数作为工具来分析图形，取得了可喜的成功。然而，这些方法过多地依赖于坐标系的选取，缺乏几何不变性，特别是用来解决某些大挠度曲线及曲线的奇异点等问题时，有一定的局限性。

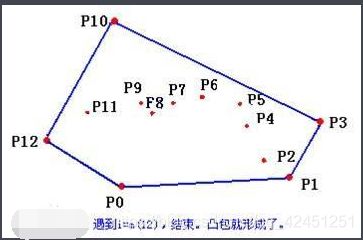
2）、推荐学习计算几何的书籍

《计算几何：算法与应用》是2005年清华大学出版社出版的图书，作者是（荷兰）德贝尔赫；《计算几何:算法与应用》(第2版)的前4章对几何算法进行了讨论，包括几何求交、三角剖分、线性规划等，其中涉及的随机算法也是《计算几何:算法与应用》(第2版)的一个鲜明特点。第5章至第10章介绍了多种几何结构，包括几何查找、kd?树、区域树、梯形图、Voronoi图、排列、Delaunay三角剖分、区间树、优先查找树以及线段树等。第11章至第16章结合实际问题，继续讨论了若干几何算法及其数据结构，包括高维凸包、空间二分及BSP树、运动规划、网格生成及四叉树、最短路径查找及可见性图、单纯性区域查找及划分树和切分树等，这些也是对前十章内容的进一步深化

3、计算几何的描述

1）、计算几何理论中过两点的一条直线的表达式，是如何描述的？
林君学长通过以下公式模型进行对计算几何进行形象化的描述：
$$\begin{gathered} 我们假设两个点不相同:x_1!=x_2 \\ 那么就有直线方程：y=\theta x_1+(1-\theta )x2 \end{gathered}$$

以上就是计算几何中的一条直线的表达式描述，在平面基础上添加角度，可以说又多了一个维度，计算方式便更加复杂！由于计算几何的复杂性，所以林君学长也还在继续研究中，后续持续更新该描述

2）、平面几何理论中过两点的一条直线的表达式，是如何描述的？
林君学长通过以下公式模型进行对平面几何形象化的描述：
$$\begin{gathered} 我们假设有两个点: \\ A(x_1,y_1)、B(x_2,y_2) \\ 那么这两个点确定的直线方程我们假设如下: \\ Ax+By+C=0 \\ 那么其中A为:y_2-y_1 \\ 其中B为:x_2-x_1 \\ 最后可得出常数c的结果:C=-A{x}_1-B{y}_1=x_2{y}_1-x_1{y}_2 \end{gathered}$$
以上就是计算几何的形象化描述，相信大家都能够看懂！那么通过python代码表示就如下所示：

def LineMake(X,Y):
    a = B[1]-A[1]
    b = A[0]-B[0]
    c = B[0] * A[1] - A[0] * B[1]
    l="确定的直线方程为："+str(a)+"x+"+str(b)+"y+"+str(c)+"=0"
    return l
}

运行结果如下所示：

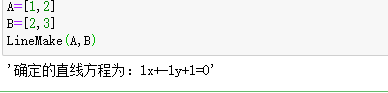
3）、与初中数学中那些直线方程（平面几何）有什么差异？有什么好处？
计算几何与平面几何（初高中学习）的区别就是维度的不一样，计算几何在平面的基础上添加了角度的维度，这意味着计算的复杂性提高了，但是计算的结果更加的广泛，更加的精确，更容易全方位的表达一条直线，举个例子说，就是我们的视觉从180度扩展到了360度

二、平面、超平面的定义及学习

1、平面的定义

1）、什么是平面？
平面，是指面上任意两点的连线整个落在此面上，一种二维零曲率广延，这样一种面，它与同它相似的面的任何交线是一条直线。是由显示生活中（例如镜面、平静的水面等）的实物抽象出来的数学概念，但又与这些实物有根本的区别,既具有无限延展性（也就是说平面没有边界），又没有大小、宽窄、薄厚之分，平面的这种性质与直线的无限延展性又是相通的

2）、平面的性质

• 公理1 如果一条直线的两个点在一个平面内，那么这条直线上的所有点都在这个平面内。
• 公理2 如果两个平面有一个公共点，那么它们还有其他公共点，这些公共点的集合是一条直线。
• 公理3 经过不在一条直线上的三个点，有且只有一个平面。
• 推论一：经过一条直线和直线外的一点，有且只有一个平面。
• 推论二：经过两条相交直线，有且只有一个平面。
• 推论三：经过两条平行直线，有且只有一个平面。

2、三维空间中的一个平面，如何表达？

1）、三维空间中的平面主要通过建立公式模型来解答，例如
$$\begin{gathered} 我们假设三维的直线方程为: \\ Ax+By+Cz+D=0 \end{gathered}$$
显而易见，我们需要的求解的便是其中的A、B、C、D的未知参量
那么我们如何求解其中的未知参量呢？便要通过特定的求解方法啦！
2）、求解未知参量A、B、C、D的方法

• 最原始的解法是根据已知的三个点，建立3个联合方程组,来消元
• 高斯消元法
• 克莱姆法则(适用于变量和方程数目相等)

其实远不止以上3中方法，还有很多的，这里林君学长给出三种显示生活中最普遍求解的方法，至于以上三种方法的求解，小伙伴们可以查阅相关资料进行求解，林君学长这里就不给出解答了，最主要查询高斯消元和克莱姆法求解方法;联合方程求解高中就接触过，较为简单！

3、超平面的定义及超平面的高维度表达

1）、什么是超平面？
超平面的数学定义是这样的：超平面H是从n维空间到n-1维空间的一个映射子空间，它有一个n维向量和一个实数定义。因为是子空间，所以超平面一定过原点。
2）、高维度超平面的表达
在数学中，超平面（Hyperplane）是n维欧氏空间中余维度等于1的线性子空间。这是平面中的直线、空间中的平面之推广。设F为域其中$$F=IR$$，
$$\begin{gathered} 则n维空间F^n中的超平面是由如下方程表示： \\ {a}_1{x}_1+...+a_n{x}_n=b \end{gathered}$$
超平面H是从n维空间到n-1维空间的一个映射子空间，它有一个n维向量和一个实数定义。设d是n维欧式空间R中的一个非零向量，a是实数，则R中满足条件dX=a的点X所组成的集合称为R中的一张超平面。

三、凸集的定义及学习

1、凸集的定义

1）、什么是凸集？
在凸几何中，凸集(convex set)是在凸组合下闭合的仿射空间的子集。更具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。例如，立方体是凸集，但是任何中空的或具有凹痕的例如月牙形都不是凸集。
特别的，凸集，实数R上（或复数C上）的向量空间中，如果集合S中任两点的连线上的点都在S内，则称集合S为凸集。


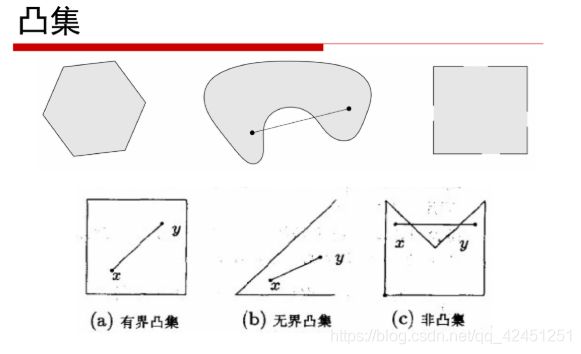
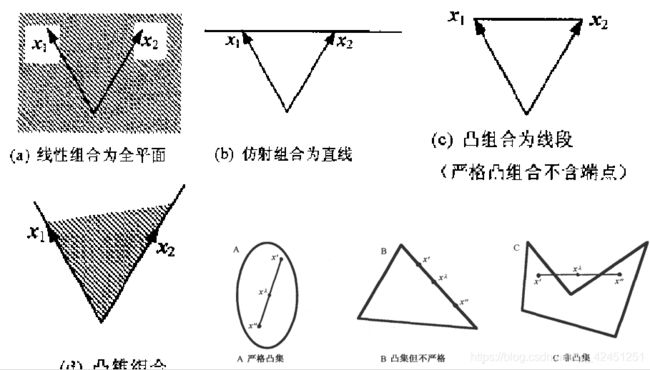
2）、在数学中凸集的数学定义？

常见的凸集：单点集 ，空集，整个欧氏空间 Rn，

2、直线是凸集吗？

凸集是单点或一条不间断的线（包括直线、射线、线段）；二、三维空间中的凸集就是直观上凸的图形。（例如：在二维中有扇面、圆、椭圆等，在三维中有实心球体等；多数情况下，两个凸集的交集也是凸集，空集也是凸集）

很显然，通过上面的凸集定义，直线肯定属于凸集啦！

3、仿射集的定义

4、直线是仿射集吗？

由上可以，直线属于仿射集，且为维数为1的仿射集

四、凸函数的定义及学习

1、凸函数的定义

1）、凸函数的简单定义
任意两点的函数值的连线上的点都在曲线的上方，我们成为凸函数。数学模型如下：

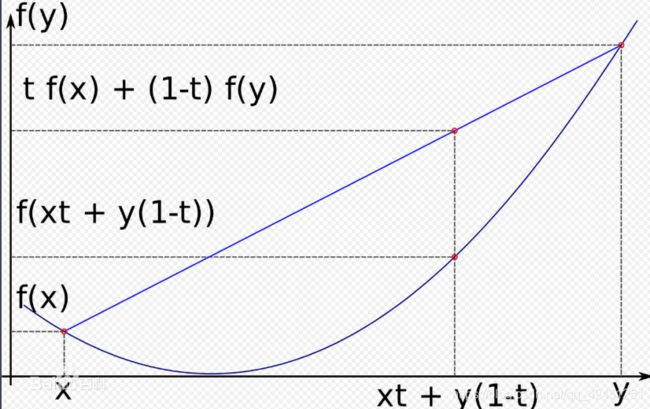
2）、凸函数的数学定义

2、Hessen矩阵定义

1）、什么是Hessen矩阵
Hessian Matrix（黑塞矩阵、海森矩阵、海瑟矩阵、海塞矩阵 etc.）,它是一个多元函数的二阶偏导数构成的方阵，用以描述函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出，并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题。

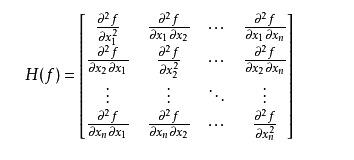
具体请参考如下链接的Hessen矩阵的讲解
https://blog.csdn.net/u010922186/article/details/41449781

3、如何判别一个函数是凸函数

1）、一元函数的判别
对于一元函数f(x)f(x)，我们可以通过其二阶导数f′′(x)f″(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0f″(x)≥0 ，则f(x)f(x)是凸函数
2）、多元函数的判别
对于多元函数f(X)f(X)，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)f(X)凸函数

4、 $f(x)=x^3$ 是凸函数吗？

1）、从公式可以看出，该函数的一元函数，那么我们便可以从一元函数的判别来进行对应的判断
2）、画出$f(x)=x^3$ 函数模型图形
画该数学模型图的python代码如下所示：

import matplotlib.pyplot as plt
import numpy as np
x=np.array([])
y=np.array([])
for i in range(-50,51,1):
    x=np.insert(x,len(x),i)
    y=np.insert(y,len(y),x[len(y)]**3)
h=1000*x
plt.plot(x,y)
plt.plot(x,h)
plt.grid()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('f(x)-y')
plt.show()

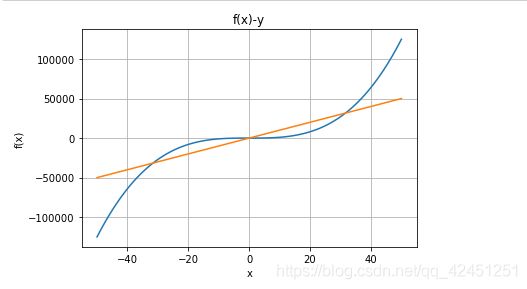
由上面的图我们可以知道，当我们用$y=1000x$的直线去截$f(x)=x^3$的模型时，我们可以看到，直线上的所有点，不都在曲线的上方，因此，该公式模型不是凸函数哦！

四、凸规划的定义及学习

1、凸规划的定义

1）、凸规划的数学定义如下所示：
设$f(x)$及$g_i(x),i=1,...,m$均为$R^n$上的凸函数，则称最优化问题为凸规划。
$$\{\begin{array}{l}min:f(x)\\ \\ s.t=\{\begin{array}{l}{g}_i(x)\le 0,i=1,2,...,m\\ \\ a_j^{T}x=b_j,j=1,2,...,p\end{array}\end{array}$$
2）、如何判别一个规划问题是凸规划问题？
与一般的最优化问题标准形式相比，凸规划有三点附加条件：
（1）目标函数$f(x)$必须是凸函数；
（2）不等式约束函数$g_i(x)$必须是凸函数，不等式$g_i(x)\le 0$组成的区域为凸集；
（3）等式约束函数$h_j(x)=a_j^{T}x-b_j$必须是仿射的（即线性函数和常函数的和函数）。
因此我们得出以下结论：凸规划的可行域是凸集。因为每个约束条件的点集都是凸集，它们的交集也是凸集。

求优化问题§ min f(x),当D为凸集，且函数f(x)为凸函数，则称该规划为凸规划。

3、验证下列(MP)是凸规划

1）、验证下列优化问题为(MP)是凸规划
$$\{\begin{array}{l}min:f(x_1,x_2,x_3)=2x_1^2+x_2^2+2x_3^2+x_1{x}_3-x_1{x}_2+x_1+2x_2\\ \\ s.t=\{\begin{array}{l}{g}_1(x)=x_1^2+x_2^2-x_3\le 0\\ \\ g_2(x)=x_1+x_2+2x_3\le 16\\ \\ g_3(x)=-x_1-x_2+x_3\le 0\end{array}\end{array}$$
2）、求解$f(x)与g_1(x)、g_2(x)、g_3(x)的$Hessen矩阵
$${▽}^{2}f(x)=\left\{\begin{array}{ccc}\frac{{\partial }^{2}f}{{\partial }^2{x}_1^2}& \frac{{\partial }^{2}f}{{\partial }^2{x}_1{x}_2}& \frac{{\partial }^{2}f}{{\partial }^2{x}_1{x}_3}\\ \frac{{\partial }^{2}f}{{\partial }^2{x}_2{x}_1}& \frac{{\partial }^{2}f}{{\partial }^2{x}_2^2}& \frac{{\partial }^{2}f}{{\partial }^2{x}_2{x}_3}\\ \frac{{\partial }^{2}f}{{\partial }^2{x}_3{x}_1}& \frac{{\partial }^{2}f}{{\partial }^2{x}_3{x}_2}& \frac{{\partial }^{2}f}{{\partial }^2{x}_3^2}\end{array}\right\}=\left[\begin{array}{ccc}4& -1& 1\\ -1& 2& 0\\ 1& 0& 4\end{array}\right]=正定、凸函数$$
$${▽}^2{g}_1(x)=\left\{\begin{array}{ccc}\frac{{\partial }^2{g}_1}{{\partial }^2{x}_1^2}& \frac{{\partial }^2{g}_1}{{\partial }^2{x}_1{x}_2}& \frac{{\partial }^2{g}_1}{{\partial }^2{x}_1{x}_3}\\ \frac{{\partial }^2{g}_1}{{\partial }^2{x}_2{x}_1}& \frac{{\partial }^2{g}_1}{{\partial }^2{x}_2^2}& \frac{{\partial }^2{g}_1}{{\partial }^2{x}_2{x}_3}\\ \frac{{\partial }^2{g}_1}{{\partial }^2{x}_3{x}_1}& \frac{{\partial }^2{g}_1}{{\partial }^2{x}_3{x}_2}& \frac{{\partial }^2{g}_1}{{\partial }^2{x}_3^2}\end{array}\right\}=\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 0\end{array}\right]=半正定、凸函数$$
$${▽}^2{g}_2(x)=\left\{\begin{array}{ccc}\frac{{\partial }^2{g}_2}{{\partial }^2{x}_1^2}& \frac{{\partial }^2{g}_2}{{\partial }^2{x}_1{x}_2}& \frac{{\partial }^2{g}_2}{{\partial }^2{x}_1{x}_3}\\ \frac{{\partial }^2{g}_2}{{\partial }^2{x}_2{x}_1}& \frac{{\partial }^2{g}_2}{{\partial }^2{x}_2^2}& \frac{{\partial }^2{g}_2}{{\partial }^2{x}_2{x}_3}\\ \frac{{\partial }^2{g}_2}{{\partial }^2{x}_3{x}_1}& \frac{{\partial }^2{g}_2}{{\partial }^2{x}_3{x}_2}& \frac{{\partial }^2{g}_2}{{\partial }^2{x}_3^2}\end{array}\right\}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]=半正定、凸函数$$
$${▽}^2{g}_3(x)=\left\{\begin{array}{ccc}\frac{{\partial }^2{g}_3}{{\partial }^2{x}_1^2}& \frac{{\partial }^2{g}_3}{{\partial }^2{x}_1{x}_2}& \frac{{\partial }^2{g}_3}{{\partial }^2{x}_1{x}_3}\\ \frac{{\partial }^2{g}_3}{{\partial }^2{x}_2{x}_1}& \frac{{\partial }^2{g}_3}{{\partial }^2{x}_2^2}& \frac{{\partial }^2{g}_3}{{\partial }^2{x}_2{x}_3}\\ \frac{{\partial }^2{g}_3}{{\partial }^2{x}_3{x}_1}& \frac{{\partial }^2{g}_3}{{\partial }^2{x}_3{x}_2}& \frac{{\partial }^2{g}_3}{{\partial }^2{x}_3^2}\end{array}\right\}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]=半正定、凸函数$$
终上所述，该优化问题为凸规划！那么我们可以作图来看一下吧！
3）、该优化问题的python代码如下所示：

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
x1=np.array([])
x2=np.array([])
x3=np.array([])
for i in range(-100,100,1):
    x1=np.insert(x1,len(x1),i)
    x2=np.insert(x2,len(x2),i)
    x3=np.insert(x3,len(x3),i)
h=2*x1**2+x2**2+2*x3**2+x1*x3-x1*x2+x1+2*x2
h1=x1**2+x2**2-x3
h2=x1+x2+x3*2-16
h3=-x1-x1+x3
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x1,x2,h,c='r',marker='o')
ax.plot(x1,x2,h1)
ax.plot(x1,x2,h2)
ax.plot(x1,x2,h3)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel("fx")
plt.show()

4）、运行结果如下所示：

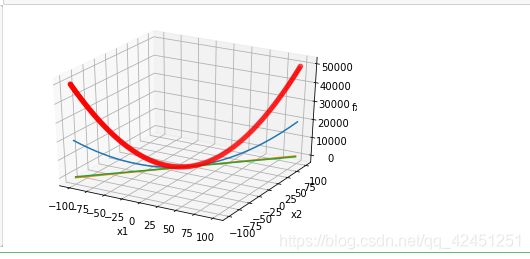
可以看出，在三维模型中，该函数肯定是凸函数，同时经过以上步骤，可得该优化问题为凸规划！

以上就是本次博客的全部内容啦，希望通过对本次博客的阅读，可以帮助小伙伴们更加容易去理解凸优化的基础理论体系，同时，我们凸性(Convexity)是最优化理论必须涉及到基本概念.具有凸性的非线性规划模型是一类特殊的重要模型，它在最优化的理论证明及算法研究中具有非常重要的作用，希望大家好好了解啦！
遇到问题的小伙伴记得评论区留言进行讨论哦，林君学长看到会给大家解答的，这个学长不太冷！
陈一月的又一天编程岁月^ _ ^