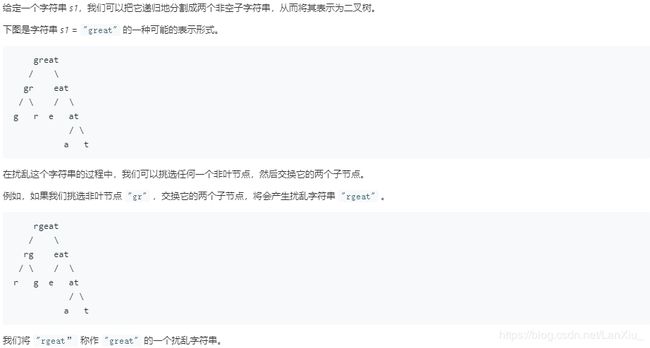
Python小白 Leetcode刷题历程 No.86-No.90 分隔链表、扰乱字符串、合并两个有序数组、格雷编码、子集Ⅱ
写在前面:
作为一个计算机院的大学生,总觉得仅仅在学校粗略的学习计算机专业课是不够的,尤其是假期大量的空档期,作为一个小白,实习也莫得路子,又不想白白耗费时间。于是选择了Leetcode这个平台来刷题库。编程我只学过基础的C语言,现在在自学Python,所以用Python3.8刷题库。现在我Python掌握的还不是很熟练,算法什么的也还没学,就先不考虑算法上的优化了,单纯以解题为目的,复杂程度什么的以后有时间再优化。计划顺序五个题写一篇日志,希望其他初学编程的人起到一些帮助,写算是对自己学习历程的一个见证了吧。
有一起刷LeetCode的可以关注我一下,我会一直发LeetCode题库Python3解法的,也可以一起探讨。
觉得有用的话可以点赞关注下哦,谢谢大家!
········································································································································································
题解框架:
1.题目,难度
2.题干,题目描述
3.题解代码(Python3(不是Python,是Python3))
4.或许有用的知识点(不一定有)
5.解题思路
6.优解代码及分析(当我发现有比我写的好很多的代码和思路我就会写在这里)
········································································································································································
No.86.分隔链表
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def partition(self, head: ListNode, x: int) -> ListNode:
dummy1 = ListNode(-1)
dummy2 = ListNode(-1)
p1 = dummy1
p2 = dummy2
while head:
if head.val < x:
p1.next = head
p1 = p1.next
else:
p2.next = head
p2 = p2.next
head = head.next
p2.next = None
p1.next = dummy2.next
return dummy1.next
或许有用的知识点:
当处理链表且需要考虑空链表时,我们或许可以设置一个哑结点,即dummy=LIstNode(-1)。
解题思路:
这道题在一个链表上操作可能比较复杂,但是分成两个链表操作就非常简单了。我们设置dummy1和dummy2两个哑节点,令p1和p2为其索引指针,将head中小于x的元素通过p1储存进链表dummy1中,其余通过p2储存进链表dummy2中。最后将dummy1和dummy2相连并输出即可。
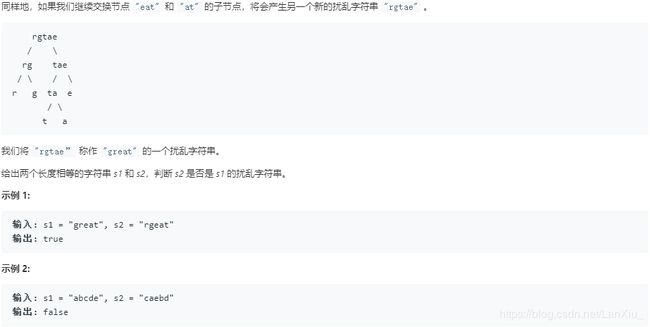
No.87.扰乱字符串
难度:困难
题目描述:
题解代码(Python3.8)
class Solution:
import functools
@functools.lru_cache(None)
def isScramble(self, s1: str, s2: str) -> bool:
if s1 == s2:
return True
if sorted(s1) != sorted(s2):
return False
for i in range(1,len(s1)):
if self.isScramble(s1[:i],s2[:i]) and self.isScramble(s1[i:],s2[i:]):
return True
if self.isScramble(s1[:i],s2[-i:]) and self.isScramble(s1[i:],s2[:-i]):
return True
return False
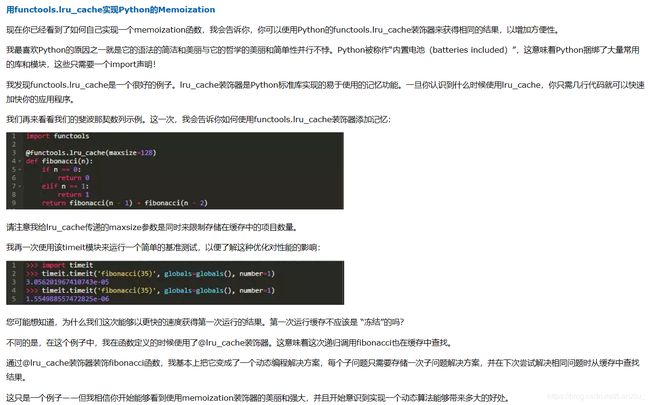
或许有用的知识点:
这其实是缓存+递归的方式,原理和动态规划一样。要用到functools.lru_cache装饰器。
解题思路:
先观察以下合乎题意的交换,因为是二叉树形式的交换,可以理解为:对于s1或s1的任意一个子结构 == 左+右,当s2或s2的任意一个子结构 == 左+右 or 右+左,都存在s1==s2。
我们用缓存+递归的方式,动态规划的原理,使用functools.lru_cache装饰器,进行高效的动态规划(自顶向下)。先特判,若 s1==s2,返回True ,若sorted(s1)!=sorted(s2),返回False。之后在[1,len(s1))的范围内,判断,如果self.isScramble(s1[:i],s2[:i]) and self.isScramble(s1[i:],s2[i:])或者if self.isScramble(s1[:i],s2[-i:]) and self.isScramble(s1[i:],s2[:-i]),返回True,否则返回False。
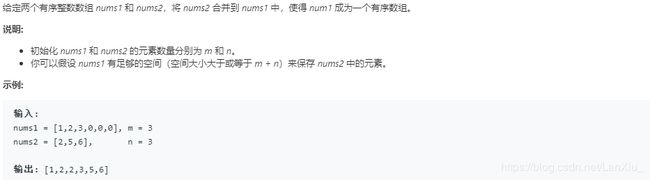
No.88.合并两个有序数组
难度:简单
题目描述:
题解代码(Python3.8)
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
i = m-1
j = n-1
for k in range(m+n-1,-1,-1):
if i == -1:
nums1[k] = nums2[j]
j -= 1
elif j == -1:
break
elif nums1[i] > nums2[j]:
nums1[k] = nums1[i]
i -= 1
else:
nums1[k] =nums2[j]
j -= 1
或许有用的知识点:
这道题要用到双指针的思想。
解题思路:
1.下面的代码使用 for 循环表示我们一个一个确定归并以后的数,从后向前归并,比较 nums1 和 nums2 末尾的元素哪个大,谁大谁出列,覆盖 nums1;
2.在 for 循环内用 if elif else 结构,保证一次只会执行一个分支;
3.分支里面先写其中一个指针遍历完成的逻辑,否则会发生数组下标越界:把 i 先用完,j 先用完的逻辑写在开头是为了防止数组下标越界,这一点不论是从前向后归并还是从后向前归并来说都是一致的;
4.从后向前归并的时候,如果 nums2 数组用完了,可以直接结束算法,因为算法如果执行下去,也是数组 nums1 自己给自己赋值,还要执行相应的判断,没有必要。
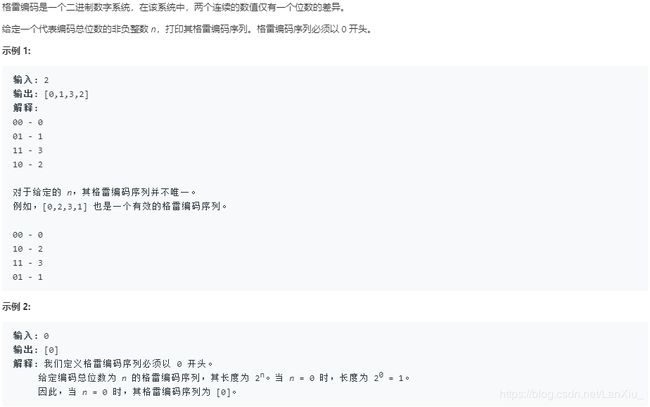
No.89.格雷编码
难度:中等
题目描述:
题解代码(Python3.8)
class Solution:
def grayCode(self, n: int) -> List[int]:
res = []
for i in range(2**n):
res.append((i >> 1) ^ i)
return res
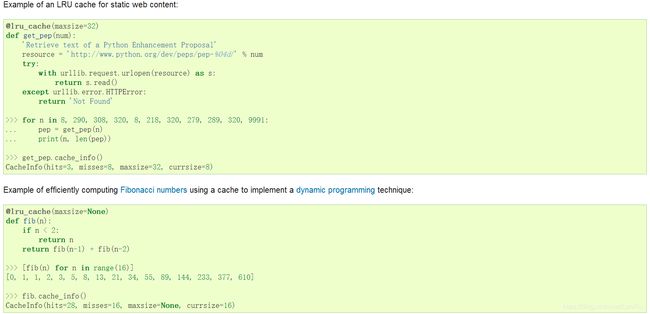
或许有用的知识点:
格雷码(Gray Code)的生成一般有两种常见的方法,一个是按照公式G[i] = B[i+1]xorB[i],另一个是采用镜射排列的方法,两种方法的具体介绍如下:
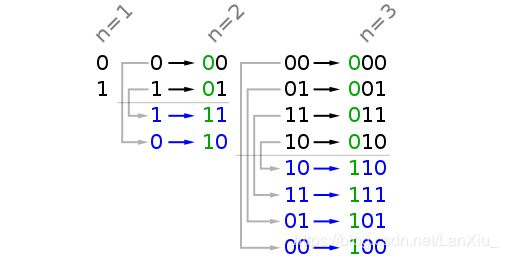
1.按照公式G[i] = B[i+1]xorB[i],简而言之,格雷码的生成满足格雷编码的生成过程, G(i) = i ^ (i/2),结合下图方便理解。
2.采用镜射排列的方法,n位元的格雷码可以从n-1位元的格雷码以上下镜射后加上新位元的方式快速的得到,如图下所示。
解题思路:
我们采用公式法生成格雷码,按照公式G[i] = B[i+1]xorB[i],逐个计算格雷码即可。
优解代码及分析:
优解代码(Python3.8)
class Solution:
def grayCode(self, n: int) -> List[int]:
res = [0]
for i in range(n):
for j in range(len(res)-1,-1,-1):
res.append( res[j] ^ (1 << i))
return res
分析: 难度:中等 题解代码(Python3.8) 或许有用的知识点: 解题思路: 其实这道题和‘No.78.子集’思路很相似,‘No.78.子集’是这道题的阉割版,大家可以做一下这道题练习一下。
我们采用镜射排列的方法,n位元的格雷码可以从n-1位元的格雷码以上下镜射后加上新位元的方式快速的得到,我们想将a=0b0xxxxx变成b=0b1xxxxx(x有n为),只需要令b=a^(1<No.90.子集Ⅱ
题目描述:
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
l = len(nums)
nums.sort()
def backtrack(index,tmp):
res.append(tmp)
for i in range(index,l):
if i>index and nums[i]==nums[i-1]:
continue
backtrack(i+1,tmp+[nums[i]])
backtrack(0,[])
return res
这道题要用到回溯算法。
这道题与‘No.78.子集’这道题的区别就是这道题数组有重复元素,要防止产生重复子集,重复时需要进行剪枝。
这道题要返回所有可能的不重复子集,所以要用到回溯算法。先对数组排序,套用回溯算法的模板,则回溯函数的三个组成部分分别为:
1.回溯出口:这道题中所有解都是回溯出口,所以无需筛选,直接res.append(tmp)。
2.回溯主体:对于for i in range(index,l)的所有值,当i>index and nums[i]==nums[i-1]
时,说明该分支是重复的,需要剪枝,否则就进入下一个回溯状态。
3.状态返回:因为所有解都是回溯出口,所以不需要状态返回。
No.78.子集
https://blog.csdn.net/LanXiu_/article/details/104253984