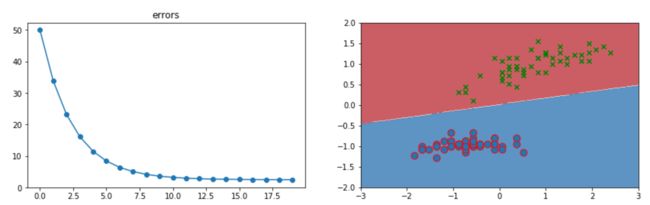
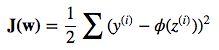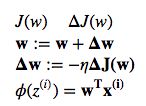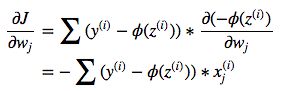损失函数与梯度,从上图可以看出梯度向下,
偏导数
可以看出计算样本y误差向量乘以样本x列向量,算出w需要使用所有的样本,然后再次迭代
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
y = df.iloc[0:100, 4].values
y = np.where(y=='Iris-setosa',1,-1)
x = df.iloc[0:100, [0,2]].values
class Perceptron():
def __init__(self, eta, X, Y, N):
self.eta = eta
self.X = X
self.Y = Y
self.N = N
self.w = [0]*len(X[0])
self.w0 = 0
self.m = len(X)
self.n = len(X[0])
def output_y(self, x):
return np.dot(x,self.w)+self.w0
def training(self):
self.errors = []
for times in xrange(self.N):
delta_y = self.Y-self.output_y(self.X)
error = (delta_y**2).sum()/2.0
self.w0 += self.eta*delta_y.sum()
self.w += self.eta*np.dot(delta_y,self.X)
self.errors.append(error)
per = Perceptron(0.0001, x, y, 300)
per.training()
print per.w0,per.w
def f(x, y):
z = per.w0+np.dot(per.w,zip(x,y))
z = np.where(z>0,1,-1)
return z
n = 200
mx = np.linspace(4, 7.5, n)
my = np.linspace(0, 6, n)
# 生成网格数据
X, Y = np.meshgrid(mx, my)
fig, axes = plt.subplots(1,2)
axes0, axes1 = axes.flatten()
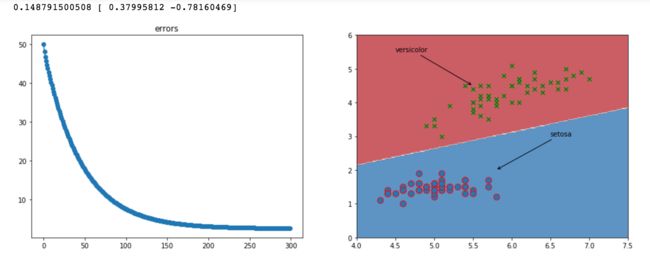
axes0.plot(per.errors, marker='o')
axes0.set_title('errors')
axes1.contourf(X, Y, f(X, Y), 2, alpha = 0.75, cmap = plt.cm.RdBu)
axes1.scatter(x[:,0][0:50], x[:, 1][0:50],s=80,edgecolors='r', marker='o')
axes1.scatter(x[:,0][50:100], x[:, 1][50:100], marker='x', color='g')
axes1.annotate(r'versicolor',xy=(5.5,4.5),xytext=(4.5,5.5),arrowprops=dict(arrowstyle='->', facecolor='blue'))
axes1.annotate(r'setosa',xy=(5.8,2),xytext=(6.5,3),arrowprops=dict(arrowstyle='->', facecolor='blue'))
fig.set_size_inches(15.5, 10.5)
plt.subplots_adjust(left=0.1, right= 0.9, bottom=0.1, top=0.5)
plt.show()
数据标准化,收敛更快
x_std = np.copy(x)
x_std[:, 0] = (x[:,0]-x[:,0].mean())/x[:,0].std()
x_std[:, 1] = (x[:,1]-x[:,1].mean())/x[:,1].std()
图形如下: