本系列教程来源于出版书籍《基于MATLAB编程基础与典型应用书籍》,如涉及版权问题,请联系:[email protected]。 出版社:人民邮电出版社, 页数:525。
本系列教程目前基于MATLABR2006a,可能对于更高级版本的功能和函数有差异,教程中如有问题,请联系:[email protected]
11.2.1 线性规划问题
线性规划问题就是由目标函数为决策变量的线性函数和约束条件为决策变量的线性等式或者线性不等式构成的优化问题,它是优化问题中比较简单的一类。在运筹学中,对于线性规划问题可以使用一些非常成熟的求解算法,包括单纯行法,对偶单纯行法,表格法等。一个标准的线性优化问题可以描述为:
在Matlab优化工具箱中,使用linprog函数对线性优化问题进行求解。其调用格式如下:
x = linprog(f,A,b)
x = linprog(f,A,b,Aeq,beq)
x = linprog(f,A,b,Aeq,beq,lb,ub)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval] = linprog(...)
[x,lambda,exitflag] = linprog(...)
[x,lambda,exitflag,output] = linprog(...)
[x,fval,exitflag,output,lambda] = linprog(...)
对于f,A,b,Aeq,Beq,lb,ub等参数在前面做了详细的叙述,x0为迭代初始值,options选项可以使用optimset和optimget命令进行设置。输出选项中一个重要的退出标志exitflag可以用来显示优化问题的求解结果退出方式。在linprog函数中,exitflag可能的退出标志及相关含义描述如表11.3所示。在这些调用格式中,如果线性规划问题中不存在不等式约束,则设置A=[],b=[];如果不存在等式约束时,则设置Aeq=[],beq=[];决策变量没有上下限的约束时,则lb=[],ub=[]。对于linprog函数,在options设置中,可以设置LargeScale为off时,使用单纯形Simplex算法对问题进行求解。
表11.3 linprog函数exitflag标志及含义描述
| exitflag标志 | 含义描述 |
|---|---|
| 1 | 函数收敛到最优解 |
| 0 | 达到最大的函数计算次数或者迭代次数 |
| -2 | 没有找到可行解 |
| -3 | 求解问题无边界约束 |
| -4 | 算法求解过程中遇到非实值Nan |
| -5 | 原问题和对偶问题均不可行 |
| -7 | 搜索方向太小 |
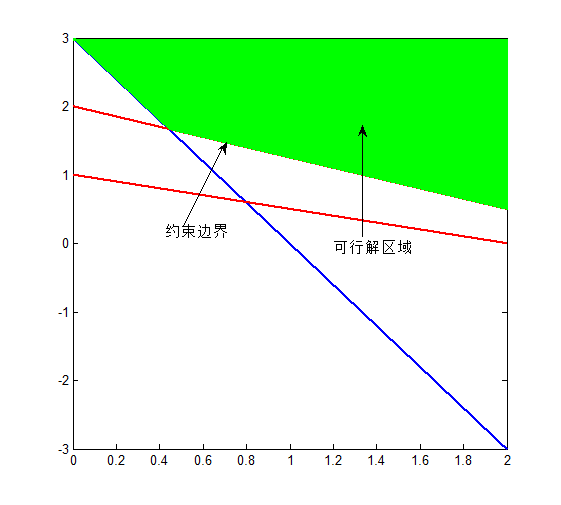
【例11.1】求解线性规划最小化问题:
如图11.1所示为规划问题约束条件确定的可行解区域,在Matlab的命令窗口中输入以下程序段:
% 目标函数系数向量
f=[2;1];
% 不等式约束系数矩阵
A=[-3 -1;-4 -3;-1 -2];
% 不等式约束常数项向量
B=[-3;-6;-2];
% 优化变量的下限
lb=[0;0];
%设置linprog函数为标准算法,显示迭代过程,采用Simplex算法
options=optimset('Simplex','on','Display','iter','LargeScale','off');
[x,fval,exitflag,output,lambda] = linprog(f,A,B,[],[],lb,[],[],options)
输出结果为:
Phase 1: Compute initial basic feasible point.
Iter Infeasibility
0 11
1 3
2 0.5
3 0
Phase 2: Minimize using simplex.
Iter Objective Dual Infeasibility
f'*x A'*y+z-w-f
0 4 3
1 2.8 0.4
2 2.4 0
Optimization terminated.
x =
0.6000
1.2000
fval =
2.4000
exitflag =
1
output =
iterations: 2
algorithm: 'medium scale: simplex'
cgiterations: []
message: 'Optimization terminated.'
lambda =
ineqlin: [3x1 double]
eqlin: [0x1 double]
upper: [2x1 double]
lower: [2x1 double]
【例11.2】求解线性规划最大化问题:
从该问题的表面上来看,为一个最大化的线性规划问题,因此首先必须将原优化问题转化为linprog可以求解的最小化问题,然后进行求解。输入以下程序段:
f=[-3;1;1]; %目标函数系数向量
A=[1 -2 1;4 -1 -2];
B=[1;-3];
Aeq=[2 0 -1];
Beq=[-1];
lb=zeros(3,1); %优化变量的下限,无上线约束
[x,fval,exitflag] = linprog(f,A,B,Aeq,Beq,lb) %求解线性规划问题
运行后,得到原优化问题达到可行解,退出标志exitflag=1,说明函数收敛到最优解。
Optimization terminated.
x =
0.6667
1.0000
2.3333
fval =
1.3333
exitflag =
1
作者:德特数据
联系方式:[email protected]