前言
这篇文章原本是我在学习计算几何学(非ICPC相关)过程中的一篇笔记。由于学校某课程的原因,经过重新整理后写出来。
在学习的过程中,参考了许多资料,包括清华大学邓老师的计算几何书籍,视频,知乎上的一些文章和各种论文,并且偷了不少图。
由于在查找资料的过程中,并没有找到一篇较为完整且较为清晰的中文资料,于是决定把这篇文章发出来。
但由于本人水平极为有限,许多地方可能是错的,仅仅代表我自己的理解。
本来计划发知乎上,结果因为知乎对markdown支持太辣鸡了所以搁置,现在又重新翻了出来。
多边形三角剖分 (Triangulation)
三角剖分有两种,一种是对多边形的三角剖分,一种是对平面点集的三角剖分。这里讨论的是对多边形的三角剖分。
美术馆问题 (Art Gallery Problem)
如何用最少的守卫看守美术馆, 并使得美术馆的每个角落都在守卫的视野之中?
一个等价的问题是:需要多少盏灯来完全照亮整个房间。
朴素的上下界
将美术馆抽象成一个多边形,那么当这个多边形存在核时,显然只需要一个守卫就能完成。
考虑最坏情况,在多边形任意顶点上都放置一个守卫,也一定可以完成。
所以守卫的数量在 到 之间。
很遗憾,对于一般多边形,求解最少需要多少守卫能够完成任务的问题是 的。
Chvátal 美术馆定理 (Chvátal Art Gallery Theorem)
将美术馆抽象为多边形,守卫抽象为点。
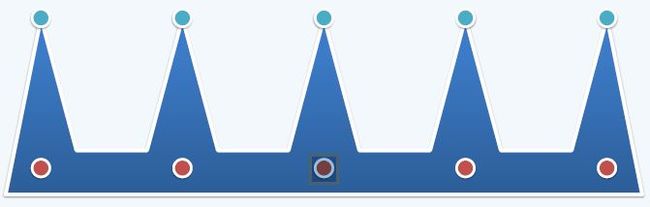
对于任意边数为 的多边形,最多只需要 个点就一定能完全覆盖了。而且存在多边形确实需要 个点才能覆盖。
如上图所示,每一个尖端都需要一个点进行覆盖。这种情况是最坏情况。
如何证明没有更坏的情况?
Fisk 的简短证明
显然对于一个三角形只需要在其一个顶点上放置一个点就可以覆盖这个三角形。
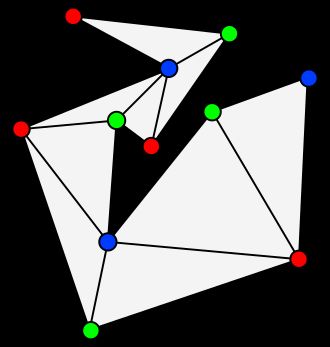
引入若干条不相交的对角线(diagonal)对多边形进行三角剖分。对角线的定义为:连接多边形一对顶点的线段。
可以证明:任何一个顶点数量为 的简单多边形都存在一个三角剖分,使其分解为 个三角形。
证明可以使用数学归纳法的思想。任取多边形的一条对角线,将多边形切分为顶点数量分别为 , 的多边形,有 且 ,又根据假设: 个顶点的简单多边形能分解为 个三角形。所以包含的三角形数量为 个。
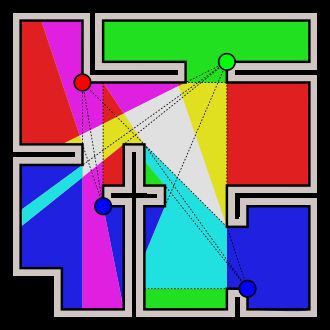
将多边形三角剖分后,形成了一张图 ,点集为多边形的顶点,边集为多边形的边和对角线的并集。观察 的对偶图,容易看出是一棵树。所以对于 一定能够进行三染色。
对于相邻的两个三角形,不重合的两个点染色必定相同,而且每个三角形的三个顶点必须一一对应这三种颜色。所以从任意三角形开始反复迭代即可完成对整张图的三染色。
在这三种颜色中,任选一种颜色就可以完成覆盖。根据鸽巢原理,最多选择 个点就足够了。
以上是美术馆问题的一个近似解,指出对于任意 个点的简单多边形,虽然求解最少使用多少点进行全覆盖是 的,但是可以证明可以使用不超过 个点进行全覆盖。
在证明的过程中使用了三角剖分这一经典的几何算法,但是对于三角剖分的一些细节还没有考虑。比如:是否任意简单多边形都能进行三角剖分?如果简单多边形带洞,是否依然能三角剖分?
三角剖分
首先界定研究对象,这里的三角剖分指的是对简单的,可以带空洞的多边形的三角剖分。
简单多边形是边不相交的多边形,根据 曲线定理,这样的多边形将平面分为一个外部区域和内部区域。
规定:对于不带洞的简单多边形,沿着边逆时针走一圈为正方向。对于带洞的简单多边形,沿着外边界逆时针走一圈为正方向,沿着内部的洞顺时针走一圈为正方向。
这样能够保证任何时刻沿着边界前进时,内部区域都在左手侧。
双耳定理 (Two Ears theorem)
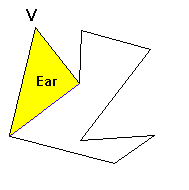
耳:对于多边形中相邻的三个顶点 ,如果向量 且 不包含任意其他顶点,则 三点构成一个耳。直观的看就是三个点满足局部凸性而且内部是空的。
对于一个多边形,可以割去一个耳,会在不改变其他性质的情况下,使得多边形的顶点数减小。
双耳定理指出对于任意简单多边形,至少有两个耳。
证明使用了数学归纳法,这里略。实际上证明的思路和下面的三角剖分构造的思路是一样的。
三角剖分存在性的证明
使用数学归纳法。
对于一个多边形,有两种属性,顶点数 和空洞数 。
基础情况: 时,多边形本身就是三角形,显然存在三角剖分。
假设:对于一个顶点数为 , 空洞数为 的多边形。任意满足: 或 的多边形都存在三角剖分。
实际上这是一个全序关系,对于任意两个多边形,能够基于这个关系进行比较。
考虑多边形 最下面的一个顶点 (如果有多个最下面的点,取最左边的一个点),有两种情况。
如果 是一个耳,那么直接切去,化为顶点数为 的多边形。
-
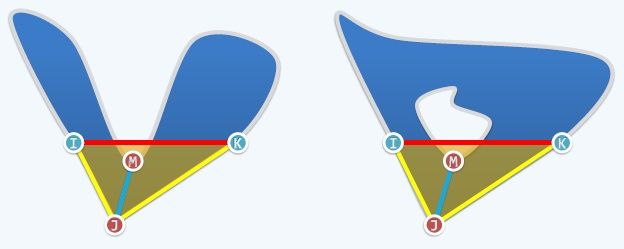
如果 不是耳,那么找到多边形其他点中距离 最近的一个点 ,连接 进行切开,又有两种情况:
- 如上图左所示, 在外边界上,那么多边形将化为两个规模更小的多边形。
- 如上图右所示, 在空洞上,新的多边形虽然顶点数量增加了,但是空洞的数量减少了。基于上面的全序关系,新多边形和原来相比规模更小。
根据归纳假设,规模更小的多边形存在三角剖分,那么多边形 也存在三角剖分。证明结束。
一些其他性质
唯一性:
不唯一,最简单的凸四边形就有两种三角剖分。
三角剖分种数的最值:
最小值为 ,最简单的凹四边形只有一种剖分方式,以此可以构造出其他情况。
最大值在凸多边形的时候达到。
假设多边形顶点数为 ,那么递推式为:
即对应第 项的 数。
时间复杂度
多边形的三角剖分可以在 时间复杂度内完成,下面是三角剖分算法,分为两个步骤:单调多边形分解和单调多边形内三角剖分。
单调多边形分解 (Monotone Decomposition)
多边形单调性
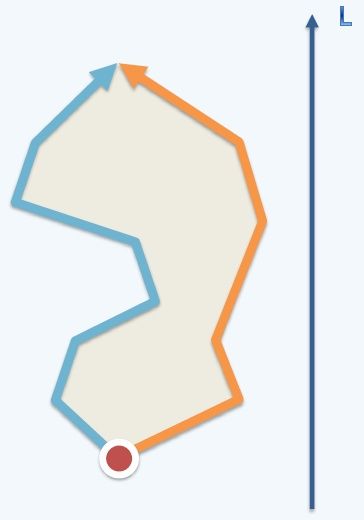
如果一条链上每条线段对于一条直线 的投影只在折点处相交,那么折线对直线 具有单调性。
如果一个多边形能被分成互补的两条链,而且这两条链都对直线 单调,那么这个多边形对 单调。
为了方便,在下面的算法中,单调多边形指的是对 轴单调的多边形,正如上图所示,是一个对 轴单调的多边形。
对于一个单调多边形,可以快速而简单地进行三角剖分。但是首先必须要把整个的简单多边形分解成若干个单调多边形。
算法如下。
顶点类型定义
对于多边形上的每一个点,可以分成 类:开始点 (start vertex),结束点(end vertex),分裂点 (split vertex),合并点 (merge vertex)和普通点 (regular vertex)。
假设当前点为,其前驱为,后继为。并且为了方便,我们假设任意两个点之间的纵坐标不同,虽然对于纵坐标相同的情况,这个算法依然正确。
- 开始点:当且仅当 和 都在 下方,并且内角 。
- 结束点:当且仅当 和 都在 上方,并且内角 。
- 分裂点:当且仅当 和 都在 下方,并且内角 。
- 合并点:当且仅当 和 都在 下方,并且内角 。
- 普通点:不满足前 种的全都是普通点。
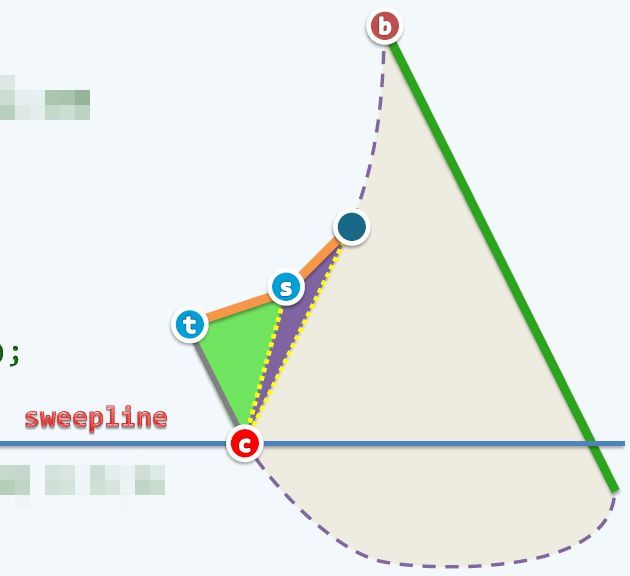
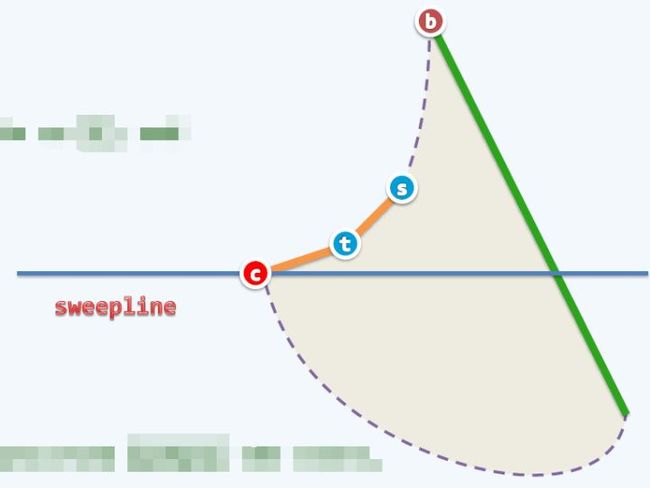
分裂点和合并点是破坏多边形单调性的原因,所以需要在这两个点的地方引进一条内对角线,将多边形拆分成两个小的多边形,以此来保证两个小多边形是单调的。显然对于分裂点,我们需要向上引入一条内对角线,对于合并点,需要向下引入一条内对角线。
以分裂点为例,如上图所示,在分裂点 处,我们需要找到在左右边境内上方最近的第一个点,图中为 ,然后引入一条内对角线,与此同时,原本的大多边形也会分裂成两个小多边形。
需要注意的是左右边界,并不是上方最近的第一个点就是我们要找的 ,因为这个点可能出现在其他小多边形中。所以我们需要维护多个小多边形的边界,并且能够查找和修改。
对于合并点,处理方法也是大同小异的。于是我们的算法就呼之欲出了。
扫描线 (sweep line)算法
设置一条水平扫描线,从上向下依次扫过每个顶点。对于每个点,按照其类型进行操作。对于开始点,结束点和普通点,维护小多边形的边界信息。对于分裂点,连接内对角线并且分裂多边形。
合并点也是同样如此,只不过是从下往上重新做一次。
需要的数据结构:由于我们需要查找和维护每个小多边形当前的边界,所以使用二分搜索树。
具体来说:对于第一次从上往下的扫描到的每个点,我们要做的是:
- 开始点:说明一个新的小多边形开始了,将其左右边界加入树。
- 结束点:说明一个小多边形结束了,找到结束点左右边界,从树中删除。
- 分裂点:从树中找到这个点所在多边形的左右边界和点上方最近的一个点,连接内对角线,加入两个新多边形的信息,删除旧的大多边形。
- 合并点:在这一次我们不连对角线(第二次从下到上的扫描才连),仅仅需要合并两个小多边形的边界信息成大多边形,并且加入树。
- 普通点:维护当前多边形的边界信息。
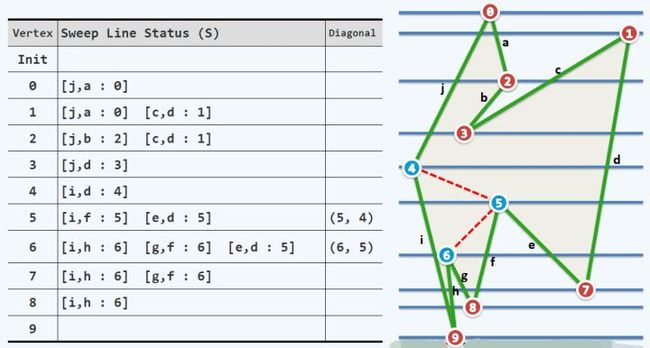
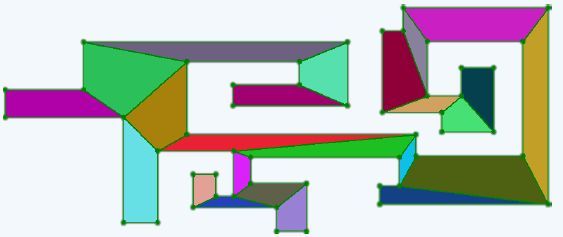
该算法较为复杂,信息量较多,可以结合下图扫描的过程手动模拟帮助理解。
代码
//写是写了,但是还没测过,手出了几组小数据好像没什么问题。
//由于偷懒用了std::set,某个地方好像复杂度有点问题,看心情修吧,先咕了。
时间复杂度
排序 ,扫描的过程中对每个点都需要查找和维护二叉平衡树,每次耗费 , 一共 个点。所以总复杂度 。
三角剖分单调多边形 (Triangulating Monotone Polygons)
由于单调多边形具有良好的性质,我们可以从贪心的想法出发,沿着多边形的左右边界逐步向下扫描,遇到一个顶点时进行操作。
单调栈
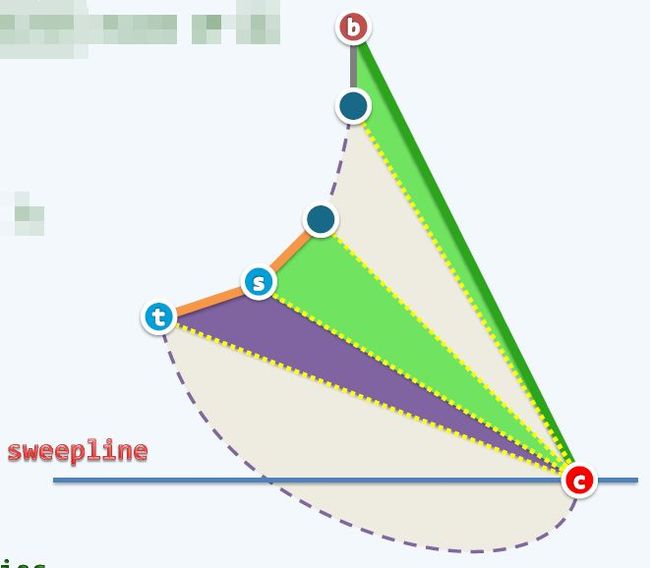
可以考虑什么情况下,当扫描到一个点时能剖分出一个三角形,什么时候不能。举个例子:
当扫描到点 时,与前面的点为异侧时,可以与前面的点依次相连进行三角剖分,直到将异侧点用完。
当扫描到点 时,与前面两个点同侧,并且形成的内角 时,可以与前两个点 相连,剖分出一个三角形,并且剖分后点 失效,如果与前两个形成的内角依然 的话,继续剖分。
当扫描到点 时,当 与前面两个点同侧,并且形成的内角 时,才不能剖分出一个三角形。
如果学过 扫描法求凸包的话,一定会发现非常相似。于是我们使用一个单调栈保存前面的点的信息,单调栈内的元素满足:
- 高度递增:因为我们从上往下扫描,所以栈顶元素一定是最低的。
- 在同一侧:如果有异侧元素出现,那么可以不停地向上剖分,直到剩下的都是同侧为止。
- 栈内连续的三个元素之间的内角 (单调性)。
扫描线算法
与上一个扫描线算法类似,从上到下设置一条水平扫描线,一开始先将最高的点加入栈,然后开始向下扫描,每个点按照上面的分类进行操作。
由于这个算法较为简单,这里不详细描述每个步骤,只给出代码。
代码
以下代码仅供参考和帮助理解算法用,实际上许多 如三点共线,或者是两个点纵坐标相同,都没考虑,所以几乎不存在鲁棒性。这个代码仅仅能够在给定单调多边形非常正常的情况下给出正确的对角线。
输入: 个点,逆时针给出的多边形坐标: 。
输出:若干条对角线连接的两个点的编号 ,表示点 和 相连。
#include
using namespace std;
typedef double db;
const db eps = 1e-6;
int sign(db k)
{
if (k > eps)
return 1;
else if (k < -eps)
return -1;
return 0;
}
int cmp(db k1, db k2) { return sign(k1 - k2); }
struct point
{
db x, y;
point operator+(const point &k1) const { return (point){k1.x + x, k1.y + y}; }
point operator-(const point &k1) const { return (point){x - k1.x, y - k1.y}; }
point operator*(db k1) const { return (point){x * k1, y * k1}; }
point operator/(db k1) const { return (point){x / k1, y / k1}; }
int operator==(const point &k1) const { return cmp(x, k1.x) == 0 && cmp(y, k1.y) == 0; }
bool operator<(const point k1) const
{
int a = cmp(y, k1.y);
if (a == -1)
return 0;
else if (a == 1)
return 1;
else
return cmp(x, k1.x) == 1;
}
};
db cross(point k1, point k2) { return k1.x * k2.y - k1.y * k2.x; }
db dot(point k1, point k2) { return k1.x * k2.x + k1.y * k2.y; }
//--------------------------------------------------------
const int maxn = 1e5 + 10;
int side[maxn];
vector> TriangulateMonotonePolygon(vector> v)
{
if (v.size() <= 3)
return {};
vector> ans;
int n = v.size();
auto vv = v;
sort(vv.begin(), vv.end());
for (int i = (vv[0].second + 1) % n; i < vv[n - 1].second; i = (i + 1) % n)
side[i] = 0; //* left: 0 right: 1
for (int i = (vv[n - 1].second + 1) % n; i < vv[0].second; i = (i + 1) % n)
side[i] = 1;
sort(v.begin(), v.end());
stack> st;
st.push(v[0]);
st.push(v[1]);
for (int i = 2, sd = side[v[i].second]; i < n - 1; i++)
{
if (side[v[i].second] == side[st.top().second]) //same side
{
if (st.size() < 2)
{
st.push(v[i]);
continue;
}
while (st.size() >= 2)
{
auto top = st.top();
st.pop();
auto top2 = st.top();
if (sd == 0 && sign(cross(top.first - top2.first, v[i].first - top.first)) == -1 ||
(sd == 1 && sign(cross(top.first - top2.first, v[i].first - top.first)) == 1))
{
st.push(top);
break;
}
ans.emplace_back(v[i].second, top2.second);
}
st.push(v[i]);
}
else
{
auto top = st.top();
while (st.size() > 1)
{
ans.emplace_back(v[i].second, st.top().second);
st.pop();
}
st.pop();
st.push(top);
st.push(v[i]);
}
}
int cnt = st.size(), now = st.size();
while (!st.empty())
{
if (now == cnt || now == 1)
{
st.pop();
continue;
}
ans.emplace_back(v[n - 1].second, st.top().second);
st.pop();
}
return ans;
}
vector> input;
int main()
{
int n;
cin >> n;
input.resize(n);
for (int i = 0; i < n; i++)
cin >> input[i].first.x >> input[i].first.y, input[i].second = i;
auto ans = TriangulateMonotonePolygon(input);
cout << "diagonal id:" << endl;
for (auto x : ans)
cout << x.first << " " << x.second << endl;
}
时间复杂度
排序 。单调栈由于每个点只会入栈出栈一次,均摊 ,有 个点,所以 。 总复杂度 。
实际上,如果给定的单调多边形已经排好序,并且标好左右边界的标记,可以把排序的复杂度去掉,这一部分的总复杂度就变为 。而这一步可以在单调多边形分解时做到。
其他
正交多边形 (Orthogonal Polygon) 覆盖
正交多边形指的是所有边都互相垂直或平行的多边形。
与三角剖分类似,由于正交多边形自身良好的性质,可以做到 个点就可以完全覆盖,采用的是凸四边形剖分。
四面体剖分 (Tetrahedralization)
当情况推广为高维,对于一个空间中的多面体,是否能够进行四面体剖分呢?
答案是否。实际上不仅做不到四面体剖分,甚至不能保证覆盖。
前面有提到,在二维多边形中,如果每个顶点都放置一个守卫,那么多边形的所有地方否会被覆盖到,然后以此继续推进,得到了最多使用 个守卫就可以全覆盖的下界。
然而在三维中,即使每个顶点都放置一个守卫,依然存在一种多面体,使得某些位置无法被覆盖。
一个著名的例子是 。
改进
在这里介绍的三角剖分算法总的时间复杂度为 。算法复杂度的瓶颈在于排序。
实际上, 年 (永远滴神) 提出了更加优秀的 算法。
借助随机化技术, 提出了 的算法。这种算法基于梯形分解 (trapezoidal decomposition),在前面介绍单调多边形分解时,其实已经有了梯形分解的雏形。这种算法不仅运行更快而且更为简单。
最后, 在 年圆满地解决了这个问题,他给出了一个线性时间的确定性算法。但是他的论文非常晦涩难懂,据我所知,可能还没有人在工业上使用这个算法。
总结
本来是一篇笔记,写着写着就变得正式了。。。
这篇文章从美术馆问题入手,先讨论了平面简单多边形的覆盖问题,然后引入三角剖分的概念和其算法。介绍了一种时间复杂度 的三角剖分算法。
算法分为两部分:单调多边形分解和单调多边形的三角剖分。 描述了算法的大致流程并且给出了部分代码。
虽然有时间复杂度更低的算法,但是相差并不特别明显。本文介绍的算法较为简单并且能够大致说明三角剖分算法的主要思想。
参考资料
- 计算几何——算法与应用,邓俊辉译,清华大学出版社
- Polygon Triangulation,Daniel Vlasic,MIT CSIAL,http://groups.csail.mit.edu/graphics/classes/6.838/F01/lectures/PolygonTriangulation/
- 计算几何第三周:三角剖分(Triangulation),z文聿,https://zhuanlan.zhihu.com/p/33737417
- Polygon triangulation,Wikipedia,https://en.wikipedia.org/wiki/Polygon_triangulation