N皇后 II
题目描述:
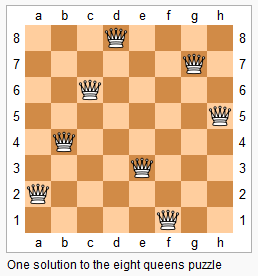
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
示例
输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解题思路:
整体思路同N皇后一致,只不过最后将结果数组的长度返回
Python源码:
class Solution:
def totalNQueens(self, n: int) -> int:
res = []
final_ans = []
ans_list = [-1 for _ in range(n)]
final_ans = list(self.queen(n,final_ans,()))
# final_ans里储存的是N皇后成功放置后的一个数字组成的元组,各个数字代表各行皇后所在的列数
for each_ans in final_ans:
final = []
for index in each_ans:
# 构建最终答案,成为题目需要的形式
row = '.'*index + 'Q'*1 + '.'*(n-index-1)
final += [row]
res.append(final)
return len(res)
def queen(self, num, final_ans, state=()):
for pos in range(num):
# pos指的是皇后当前应该放置的位置的横坐标,也就是列
if not self.conflict(state, pos):
# 如果产生皇后的位置信息
# 如果只剩下最后一个皇后没有放置
if len(state) == num - 1:
yield (pos,)
# 否则,把当前皇后的位置信息,添加到状态列表里,并且传递给下一个皇后
# 程序要从前面的皇后得到包含未知信息的元组(元组不可更改)
# 并且要求后面的皇后提供当前皇后的每一种合法的位置信息
# 所以把当前皇后的位置信息,添加到状态列表里,并传递给下一个皇后
else:
for result in self.queen(num, final_ans, state + (pos,)):
yield (pos,) + result
def conflict(self, state, nextX):
# nextY表示当前棋盘的长度,也就是下一个皇后应该落在的行的编号
nextY = len(state)
for i in range(nextY):
# 遍历之前的行,state[i]表示他们所在的列数,i表示他们所在的行数
if abs(state[i]-nextX) in (0, nextY-i):
return True
return False
欢迎关注我的github:https://github.com/UESTCYangHR