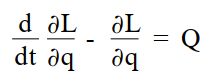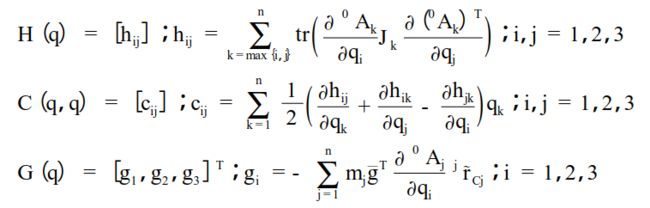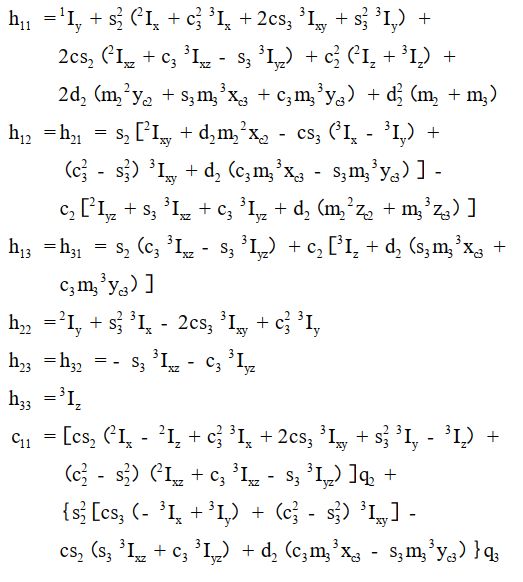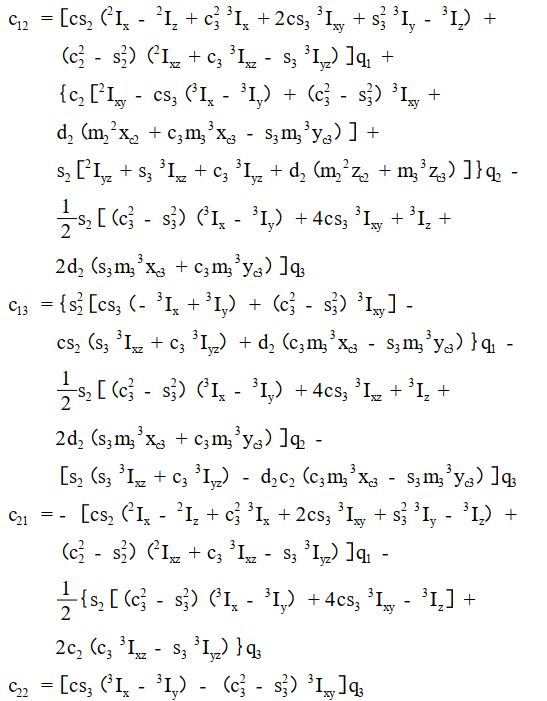1、拉格朗日法
拉格朗日法是一种基于能量的动力学方法,从拉格朗日函数L(系统动能和势能的差值)出发来建立机器人动力学方程:
应用于机器人动力学模型推导(详细过程可参考霍伟编写的《机器人动力学与控制》),最终可得出如下的形式:
式中各项H,C,G的求解算法如下,本文将该算法用Matlab实现。
2、Matlab代码
function [H,C,G] = LagrangianDynamics(dh_list, mass_list, mass_center_list, inertia_tensor_list)
[rows, columns] = size(dh_list);
number_of_links = rows;
if columns ~= 4
error('wrong DH parameters!')
end
for i = 1:rows
% 定义关节位置,速度,加速度符号
eval(['syms ','q',num2str(i),' real;']);
eval(['syms ','dq',num2str(i),' real;']);
eval(['syms ','ddq',num2str(i),' real;']);
eval(['q(i)=','q',num2str(i),';']);
eval(['dq(i)=','dq',num2str(i),';']);
eval(['ddq(i)=','ddq',num2str(i),';']);
end
A = sym([]);
for i = 1:number_of_links
dh = dh_list(i,:);
alpha(i) = dh(1);
a(i) = dh(2);
d(i) = dh(3);
q(i) = dh(4);
A(:,:,i) = [cos(q(i)), -sin(q(i))*cos(alpha(i)), sin(alpha(i))*sin(q(i)), a(i)*cos(q(i));
sin(q(i)), cos(q(i))*cos(alpha(i)), -sin(alpha(i))*cos(q(i)), a(i)*sin(q(i));
0, sin(alpha(i)), cos(alpha(i)), d(i);
0, 0, 0, 1];
end
A = simplify(A);
% 计算每个连杆坐标系在{0}系下的表达
A0 = sym([]);
for i = 1:number_of_links
A0(:,:,i) = eye(4,4);
for j = 1:i
A0(:,:,i) = A0(:,:,i)*A(:,:,j);
end
end
A0 = simplify(A0);
J = sym([]);
for i = 1:number_of_links
J(:,:,i) = JMatrix(mass_list(i),mass_center_list(1,:),inertia_tensor_list(:,:,i));
end
% 计算H(q),由H(q)对称性,只需计算上三角部分
syms tr
for i = 1:number_of_links
for j = i:number_of_links
tr = 0;
for k = j:number_of_links
tr = tr + trace(eval(['diff(A0(:,:,k),q',num2str(i),')'])*J(:,:,k)*...
eval(['diff(transpose(A0(:,:,k)),q',num2str(j),')']));
end
H(i,j) = simplify(tr);
H(j,i) = H(i,j);
end
end
% 计算C(q)
for i = 1:number_of_links
for j = 1:number_of_links
c = 0;
for k = 1:number_of_links
c = c + 1/2*(eval(['diff(H(i,j),q',num2str(k),')'])...
+ eval(['diff(H(i,k),q',num2str(j),')'])...
- eval(['diff(H(j,k),q',num2str(i),')']))*eval(['dq',num2str(k)]);
end
C(i,j) = simplify(c);
end
end
syms gc
g = [0,0,-gc,0]';
% 计算G(q)
for i = 1:number_of_links
gi = 0;
for j = 1:number_of_links
gi = gi - mass_list(j)*g'...
*eval(['diff(A0(:,:,j),q',num2str(i),')'])...
*[mass_center_list(j,:),1]';
end
G(i) = simplify(gi);
end
G = G';
end
代码中的齐次矩阵A(:,:,i)计算对应的是标准DH模型,如果杆件坐标系是用修改的DH模型建立,则只需修改A(:,:,i)的计算即可。下面的用例可测试编写的代码:
% 拉格朗日动力学方程求解测试
clc;
clear;
syms q1 q2 q3 m1 m2 m3 d2 real
syms Ix1 Iy1 Iz1 Ixy1 Iyz1 Ixz1 real
syms Ix2 Iy2 Iz2 Ixy2 Iyz2 Ixz2 real
syms Ix3 Iy3 Iz3 Ixy3 Iyz3 Ixz3 real
syms xc1 yc1 zc1 xc2 yc2 zc2 xc3 yc3 zc3 real
dh_params = [-pi/2, 0, 0, q1;
pi/2, 0, d2, q2;
0, 0, 0, q3];
mass_center = [xc1, yc1, zc1;
xc2, yc2, zc2;
xc3, yc3, zc3];
mass = [m1,m2,m3];
inertia_1 = [Ix1, Ixy1, Ixz1;
Ixy1, Iy1, Iyz1;
Ixz1, Iyz1, Iz1];
inertia_2 = [Ix2, Ixy2, Ixz2;
Ixy2, Iy2, Iyz2;
Ixz2, Iyz2, Iz2];
inertia_3 = [Ix3, Ixy3, Ixz3;
Ixy3, Iy3, Iyz3;
Ixz3, Iyz3, Iz3];
inertia_tensor(:,:,1) = inertia_1;
inertia_tensor(:,:,2) = inertia_2;
inertia_tensor(:,:,3) = inertia_3;
[h,c,g] = LagrangianDynamics(dh_params, mass, mass_center, inertia_tensor)
上面的程序基于编写的LagrangianDynamics函数求解书中的算例2-1:
代码运行后输出动力学方程中的各个系数矩阵:
h =
[ Ix2 + Iy1 + Iy3 + d2^2*m2 + d2^2*m3 - Ix2*cos(q2)^2 + Ix3*cos(q3)^2 - Iy3*cos(q2)^2 - Iy3*cos(q3)^2 + Iz2*cos(q2)^2 + Iz3*cos(q2)^2 + Ixy3*sin(2*q3) + Ixz2*sin(2*q2) - Ix3*cos(q2)^2*cos(q3)^2 + Iy3*cos(q2)^2*cos(q3)^2 + 2*d2*m2*yc1 + 2*Ixz3*cos(q2)*cos(q3)*sin(q2) - 2*Iyz3*cos(q2)*sin(q2)*sin(q3) + 2*d2*m3*yc1*cos(q3) + 2*d2*m3*xc1*sin(q3) - 2*Ixy3*cos(q2)^2*cos(q3)*sin(q3), Ixy2*sin(q2) - Iyz2*cos(q2) - Ixy3*sin(q2) - Iyz3*cos(q2)*cos(q3) - Ixz3*cos(q2)*sin(q3) + 2*Ixy3*cos(q3)^2*sin(q2) - Ix3*cos(q3)*sin(q2)*sin(q3) + Iy3*cos(q3)*sin(q2)*sin(q3) - d2*m2*zc1*cos(q2) - d2*m3*zc1*cos(q2) + d2*m2*xc1*sin(q2) + d2*m3*xc1*cos(q3)*sin(q2) - d2*m3*yc1*sin(q2)*sin(q3), Iz3*cos(q2) + Ixz3*cos(q3)*sin(q2) - Iyz3*sin(q2)*sin(q3) + d2*m3*yc1*cos(q2)*cos(q3) + d2*m3*xc1*cos(q2)*sin(q3)]
[ Ixy2*sin(q2) - Iyz2*cos(q2) - Ixy3*sin(q2) - Iyz3*cos(q2)*cos(q3) - Ixz3*cos(q2)*sin(q3) + 2*Ixy3*cos(q3)^2*sin(q2) - Ix3*cos(q3)*sin(q2)*sin(q3) + Iy3*cos(q3)*sin(q2)*sin(q3) - d2*m2*zc1*cos(q2) - d2*m3*zc1*cos(q2) + d2*m2*xc1*sin(q2) + d2*m3*xc1*cos(q3)*sin(q2) - d2*m3*yc1*sin(q2)*sin(q3), Ix3/2 + Iy2 + Iy3/2 - (Ix3*cos(2*q3))/2 + (Iy3*cos(2*q3))/2 - Ixy3*sin(2*q3), - Iyz3*cos(q3) - Ixz3*sin(q3)]
[ Iz3*cos(q2) + Ixz3*cos(q3)*sin(q2) - Iyz3*sin(q2)*sin(q3) + d2*m3*yc1*cos(q2)*cos(q3) + d2*m3*xc1*cos(q2)*sin(q3), - Iyz3*cos(q3) - Ixz3*sin(q3), Iz3]
c =
[ dq2*(Iyz3*sin(q3) - Ixz3*cos(q3) - Ixz2 + 2*Ixz2*cos(q2)^2 + (Ix2*sin(2*q2))/2 + (Iy3*sin(2*q2))/2 - (Iz2*sin(2*q2))/2 - (Iz3*sin(2*q2))/2 + 2*Ixz3*cos(q2)^2*cos(q3) - 2*Iyz3*cos(q2)^2*sin(q3) + Ix3*cos(q2)*cos(q3)^2*sin(q2) - Iy3*cos(q2)*cos(q3)^2*sin(q2) + 2*Ixy3*cos(q2)*cos(q3)*sin(q2)*sin(q3)) - dq3*(Ixy3 - Ixy3*cos(q2)^2 - 2*Ixy3*cos(q3)^2 + (Ix3*sin(2*q3))/2 - (Iy3*sin(2*q3))/2 + 2*Ixy3*cos(q2)^2*cos(q3)^2 + Iyz3*cos(q2)*cos(q3)*sin(q2) + Ixz3*cos(q2)*sin(q2)*sin(q3) - d2*m3*xc1*cos(q3) + d2*m3*yc1*sin(q3) - Ix3*cos(q2)^2*cos(q3)*sin(q3) + Iy3*cos(q2)^2*cos(q3)*sin(q3)), dq1*(Iyz3*sin(q3) - Ixz3*cos(q3) - Ixz2 + 2*Ixz2*cos(q2)^2 + (Ix2*sin(2*q2))/2 + (Iy3*sin(2*q2))/2 - (Iz2*sin(2*q2))/2 - (Iz3*sin(2*q2))/2 + 2*Ixz3*cos(q2)^2*cos(q3) - 2*Iyz3*cos(q2)^2*sin(q3) + Ix3*cos(q2)*cos(q3)^2*sin(q2) - Iy3*cos(q2)*cos(q3)^2*sin(q2) + 2*Ixy3*cos(q2)*cos(q3)*sin(q2)*sin(q3)) + dq2*(Ixy2*cos(q2) - Ixy3*cos(q2) + Iyz2*sin(q2) + Iyz3*cos(q3)*sin(q2) + Ixz3*sin(q2)*sin(q3) + 2*Ixy3*cos(q2)*cos(q3)^2 - Ix3*cos(q2)*cos(q3)*sin(q3) + Iy3*cos(q2)*cos(q3)*sin(q3) + d2*m2*xc1*cos(q2) + d2*m2*zc1*sin(q2) + d2*m3*zc1*sin(q2) + d2*m3*xc1*cos(q2)*cos(q3) - d2*m3*yc1*cos(q2)*sin(q3)) - (dq3*sin(q2)*(Iz3 + Ix3*(2*cos(q3)^2 - 1) - Iy3*(2*cos(q3)^2 - 1) + 4*Ixy3*cos(q3)*sin(q3) + 2*d2*m3*yc1*cos(q3) + 2*d2*m3*xc1*sin(q3)))/2, - dq3*(Iyz3*cos(q3)*sin(q2) + Ixz3*sin(q2)*sin(q3) - d2*m3*xc1*cos(q2)*cos(q3) + d2*m3*yc1*cos(q2)*sin(q3)) - dq1*(Ixy3 - Ixy3*cos(q2)^2 - 2*Ixy3*cos(q3)^2 + (Ix3*sin(2*q3))/2 - (Iy3*sin(2*q3))/2 + 2*Ixy3*cos(q2)^2*cos(q3)^2 + Iyz3*cos(q2)*cos(q3)*sin(q2) + Ixz3*cos(q2)*sin(q2)*sin(q3) - d2*m3*xc1*cos(q3) + d2*m3*yc1*sin(q3) - Ix3*cos(q2)^2*cos(q3)*sin(q3) + Iy3*cos(q2)^2*cos(q3)*sin(q3)) - (dq2*sin(q2)*(Iz3 + Ix3*(2*cos(q3)^2 - 1) - Iy3*(2*cos(q3)^2 - 1) + 4*Ixy3*cos(q3)*sin(q3) + 2*d2*m3*yc1*cos(q3) + 2*d2*m3*xc1*sin(q3)))/2]
[ dq3*((Ix3*sin(q2))/2 - (Iy3*sin(q2))/2 + (Iz3*sin(q2))/2 - Ixz3*cos(q2)*cos(q3) + Iyz3*cos(q2)*sin(q3) - Ix3*cos(q3)^2*sin(q2) + Iy3*cos(q3)^2*sin(q2) - 2*Ixy3*cos(q3)*sin(q2)*sin(q3)) - dq1*(Iyz3*sin(q3) - Ixz3*cos(q3) - Ixz2 + 2*Ixz2*cos(q2)^2 + (Ix2*sin(2*q2))/2 + (Iy3*sin(2*q2))/2 - (Iz2*sin(2*q2))/2 - (Iz3*sin(2*q2))/2 + 2*Ixz3*cos(q2)^2*cos(q3) - 2*Iyz3*cos(q2)^2*sin(q3) + Ix3*cos(q2)*cos(q3)^2*sin(q2) - Iy3*cos(q2)*cos(q3)^2*sin(q2) + 2*Ixy3*cos(q2)*cos(q3)*sin(q2)*sin(q3)), -dq3*(Ixy3*cos(2*q3) - (Ix3*sin(2*q3))/2 + (Iy3*sin(2*q3))/2), Ixy3*dq2 - 2*Ixy3*dq2*cos(q3)^2 + (Ix3*dq2*sin(2*q3))/2 - (Iy3*dq2*sin(2*q3))/2 - Ixz3*dq3*cos(q3) + (Ix3*dq1*sin(q2))/2 - (Iy3*dq1*sin(q2))/2 + Iyz3*dq3*sin(q3) + (Iz3*dq1*sin(q2))/2 - Ix3*dq1*cos(q3)^2*sin(q2) + Iy3*dq1*cos(q3)^2*sin(q2) - Ixz3*dq1*cos(q2)*cos(q3) + Iyz3*dq1*cos(q2)*sin(q3) - 2*Ixy3*dq1*cos(q3)*sin(q2)*sin(q3)]
[ dq1*(Ixy3 - Ixy3*cos(q2)^2 - 2*Ixy3*cos(q3)^2 + (Ix3*sin(2*q3))/2 - (Iy3*sin(2*q3))/2 + 2*Ixy3*cos(q2)^2*cos(q3)^2 + Iyz3*cos(q2)*cos(q3)*sin(q2) + Ixz3*cos(q2)*sin(q2)*sin(q3) - d2*m3*xc1*cos(q3) + d2*m3*yc1*sin(q3) - Ix3*cos(q2)^2*cos(q3)*sin(q3) + Iy3*cos(q2)^2*cos(q3)*sin(q3)) - dq2*((Ix3*sin(q2))/2 - (Iy3*sin(q2))/2 + (Iz3*sin(q2))/2 - Ixz3*cos(q2)*cos(q3) + Iyz3*cos(q2)*sin(q3) - Ix3*cos(q3)^2*sin(q2) + Iy3*cos(q3)^2*sin(q2) - 2*Ixy3*cos(q3)*sin(q2)*sin(q3)), dq2*(Ixy3*(2*cos(q3)^2 - 1) - Ix3*cos(q3)*sin(q3) + Iy3*cos(q3)*sin(q3)) - dq1*((Ix3*sin(q2))/2 - (Iy3*sin(q2))/2 + (Iz3*sin(q2))/2 - Ixz3*cos(q2)*cos(q3) + Iyz3*cos(q2)*sin(q3) - Ix3*cos(q3)^2*sin(q2) + Iy3*cos(q3)^2*sin(q2) - 2*Ixy3*cos(q3)*sin(q2)*sin(q3)), 0]
g =
0
-gc*(m2*xc2*cos(q2) + m2*zc2*sin(q2) + m3*zc3*sin(q2) + m3*xc3*cos(q2)*cos(q3) - m3*yc3*cos(q2)*sin(q3))
gc*m3*sin(q2)*(yc3*cos(q3) + xc3*sin(q3))
对比书中给出的结果,经过适当变形,可以看出是一致的,代入到文章开头的运动方程,即可获得该机械臂显式的动力学方程。