TensorFlow Quantum 使用心得

特邀博文 / Owen Lockwood，来自伦斯勒理工学院

 

量子力学曾是一门富有争议的学说。早期的批判者（如爱因斯坦）曾在量子力学领域留下一句名言，即“上帝不会掷骰子”（指的是量子测量的概率特性），尼尔斯·玻尔对此评论道：“爱因斯坦，不要对上帝指手画脚。”然而大家都同意爱因斯坦的观点，引用约翰·惠勒的一句话就是，“如果你不曾为量子力学困惑不已，则将无法领略其中的真谛”。

随着对量子力学的认识不断深入，我们不仅从中收获到许多重要的物理发现，同时也通过量子力学催生了量子计算领域。量子计算是一门与传统计算不同的计算范式。此领域以量子力学原理为基础，并不断加以开发，从而可获得比使用传统计算机更快的速度（在某些情况下可实现超多项式时间）。

在这篇文章中，我会聊聊自己在开始研究量子机器学习 (QML) 时面临到的一些挑战，以及我通过 TensorFlow Quantum (TFQ) 和 Cirq 受益并帮助其他研究人员探索量子计算和 QML 领域的方法。因为我之前接触过 TensorFlow，所以使用 TensorFlow Quantum 对我来说也是轻车熟路。事实证明，TFQ 对我完成工作很有帮助，然后终于在第 16 届 AIIDE 会议上，我在量子强化学习领域用 TFQ 发表了我的首个作品，而那则是我最辉煌的时刻。我希望这篇文章可以帮助和激励其他研究人员、新手和专家，使其通过 TFQ 进一步推动 QML 领域的发展。

 

QML 背景

QML 和机器学习在传统神经网络/深度学习方法方面有着重要的相似性和不同点。这两种方法均可看做是使用了转换的“堆叠层”，而这正是较大模型的构成要素。在这两种情况下，我们通常会为了最小化某些损失函数，将数据用于通知模型参数更新（大多情况下是这样，但不完全都是通过基于梯度的方法）。这两种方法的不同之处在于，QML 模型可以利用量子力学的力量，而深度神经网络则不能。我们会将一种由 TFQ 提供技术支持的重要 QML 称作变分量子电路 (QVC)。QVC 也可称作量子神经网络 (QNN)。

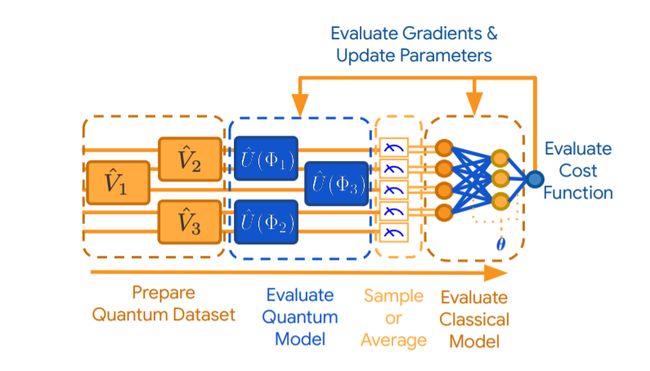
QVC 如下图所示（来自 TFQ 白皮书）。图表阅读顺序为从左往右，其中量子位由水平横线表示。QVC 可分为三个重要而又不同的部分：编码器电路、变分电路和测量运算符。编码器电路可以接收自然量子数据（如非参数化量子电路），或将传统数据转化为量子数据。编码器电路连接到变分电路，后者由其可学习参数定义。在学习过程中更新的部分即为电路的参数化部分。QVC 最后的组成部分为测量运算符。如要从 QVC 中提取信息，必须应用某种量子测量方法（如 Pauli X、Y 或 Z 基的测量）。通过使用提取自这些测量方法中的信息，我们得以在传统计算机上计算损失函数（以及梯度）并更新参数。同时，可通过类似传统神经网络（如 Adam 或 RMSProp）的优化器来优化这些梯度。QVC 也可与传统神经网络相结合（如图所示），因为量子电路具备可微分性，因此梯度可以反向进行传播。

 

然而围绕 QVC 的直观模型和数学框架与传统神经网络有一些重要区别，而在这些差异中存在着量子加速的潜能。量子计算和 QML 可以对量子现象加以利用，如叠加和纠缠。叠加源自于波函数，而波函数是多个状态的线性组合，可让量子位同时呈现出两种不同的状态（以概率的方式）。能够在此类叠加上采取操作（即同时对多个状态进行操作）是量子力学计算不可或缺的一部分。纠缠是一种通过多量子位门生成的复杂现象。对这些概念和量子计算具有基本的了解是使用 QML 的重要前提。这里有关于上述内容的大量可用资源，如 Preskill 的量子计算课程和 de Wolf 的讲义。

不过目前想要使用真正的量子硬件，条件极为有限，因此很多量子计算研究人员都在模拟的量子计算机上进行工作。近期和当前的量子设备都具备 10 到 100 个量子位 (qubit)，如 Google Sycamore 处理器。因其外观尺寸和产生的噪音，这种硬件通常又被称为嘈杂中型量子 (NISQ) 技术。TFQ 和 Cirq 即是为这些近期的 NISQ 设备量身打造而成。鉴于当前的纠错技术，这些设备要比某些通过著名量子算法实现量子加速的设备小得多；例如，秀尔算法需要上千个量子位，而量子近似优化算法 (QAOA) 可能至少需要 420 个量子位才能获得量子优势。然而 NISQ 设备在实现量子加速方面仍有巨大潜能（如 Google 通过 53 个量子位进行验证地那样）。

 

TFQ 和我的工作

TFQ 于今年（2020 年）3 月中旬发布，发布后不久我便开始使用。自那时起，我就已开始研究 QML，并格外关注了用于强化学习 (RL) 的 QML。尽管我已经在量子电路模拟器的无障碍功能方面取得了巨大进步，但是仍然很难踏入 QML 这一领域。除了在数学和物理方面遇到的困难，根本困难则是位实现成果所投入的时间。对于那些从事传统机器学习的研究人员来说，从头开始编写 QVC 所需的时间，以及正确测试和调试 QVC 花费的时间（更不用说优化）都是一种挑战。花费大量时间去构建一个可能会失败的试验品，对我来说风险巨大，尤其我当时还是一个即将毕业的大学生！幸运的是，我不用冒这个险。随着 TFQ 的发布，我可以在其中轻松即时地将我的想法转变为现实。实际上，如果 TFQ 不曾发布，那我可能永远也无法完成这项工作。受先前工作的启发，我们扩展性地在 RL 任务中应用了 QML。

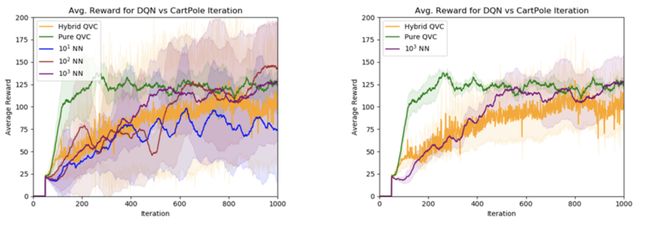
通过这一做法，我们证明了在当代 RL 算法中使用 QVC 代替神经网络的潜力（特别是 DQN 和 DDQN）。同时我们也展示了使用多类 QVC 模型的潜力，通过使用具有密集层或量子池层（分别表示混合动力和纯动力）的 QVC 来减少正确输出空间中量子位的数量。

 

QVC 所具有的代表性效力也得以呈现；通过使用具备约 50 个参数的 QVC，我们能够收获等同于在神经网络上使用更多数量级参数所呈现的性能。从图上我们可以对比得出，在典型 CartPole 环境（让小车上的一个倒立摆保持平衡）中达成的性能，左图包括所有的神经网络，而右图只显示了最大的神经网络。NN 前面的数字代表参数空间的大小。

我们会继续在 RL 中应用 QML，并为大家呈现更多稿件。这项工作现已纳入 2020 NeurIPS 研讨会：“预注册实验：用于机器学习研究的可替换发布模型。”

 

TFQ 使用建议

无论您的背景如何，只要您对 QML 研究感兴趣，那 TFQ 对您来说都将是一个极佳的工具。在科学界，拥有“发表或者灭亡”的心态早已习以为常，不过这可能会扼杀创新工作并抑制思维的发散，对于那些需要采取大量实操工作的实验而言更是如此。TFQ 不仅可以帮助您加速实验，还可以助您轻松实现那些可能永远难以试验的想法。付诸实践是实现很多新鲜有趣想法的常见阻碍，到目前为止由于将想法转化为现实异常困难，很多想法依然停留在构想阶段，而 TFQ 则可以轻松做到这一点。

对于初学者而言，TFQ 是出色的入门工具，即使您没有大量的时间来研究编码，您依然能从中收获大量知识。无需从头开始构建，即可借助 QVC 进行尝试和实验。不得不说，这的确是一款令人难以置信的工具。对于有 TensorFlow 使用经验的传统 ML 研究人员来说，其可通过 TFQ，轻松完成对 QML 的小规模或大规模的过渡和转换。TFQ 的 API 和其提供的模块（如 Keras-esque 层和微分器）与 TF 的设计原则一致，而这一相似性则更有利于轻松完成编程转换。对于身处 QML 领域的研究人员来说，TFQ 当然也能有所助力。

如想上手使用 TFQ，则必须要熟悉量子计算的基础知识。您可以参阅上述参考资料或是除此之外的其他资源。还有另一个经常遭到忽视的重要步骤，那就是阅读 TFQ 白皮书。白皮书可供 QML 初学者使用，其中介绍了大量有关 QML 的理论知识，以及 TFQ 的基础和高级用法。阅读白皮书和使用 TFQ 同样重要。试着尝试不同的事物，如实验；通过开展实验，您不仅可以进一步了解软件，还可以加深对理论和数学的理解。通过阅读其他当代论文及引用了 TFQ 的论文，亦可让自己沉浸于该领域正在进行的研究之中。

 

推荐阅读

你可以通过阅读以下文章进一步了解 TensorFlow Quantum。

• TensorFlow Quantum 一岁啦！
• TensorFlow Quantum 模拟发现量子机器学习的优势
• “量子固件”来了，利用 TensorFlow 提升量子计算硬件性能
• 介绍量子神经网络训练策略，解决消失梯度问题
• 发布量子机器学习开源库：TensorFlow Quantum

欢迎大家关注下方 TensorFlow 官方微信公众号获取更多信息。