剑指Offer面试题:10- I 斐波那契数列
算法不是金庸武侠小说里硬核的”九阳真经“,也不是轻量的”凌波微步“,它是程序员的基本功,如同练武之人需要扎马步一般。功夫好不好,看看马步扎不扎实;编程能力强不强,看看算法能力有没有。本系列采用leetcode题号,使用JavaScript为编程语言,每篇文章都会逐步分析解题思路,最终给出代码。文章一方面是记录笔者在刷题中的思路,已备学而时习之,另一方面也希望能跟大牛们多交流。有更高效的解法,或者文章有什么问题,都欢迎提出来,望诸位不吝赐教。
目录
-
- 一、题目:斐波那契数列
- 二、小马甲思路
- 三、小马甲题解
- 四、总结
一、题目:斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) +F(N - 2), 其中 N > 1.
斐波那契数列由0和1开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回1。
示例1:
输入:n = 2
输出:1
示例2:
输入:n = 5
输出:5
提示:
- 0 <= n <= 100
二、小马甲思路
看看这定义
F(0) = 0, F(1) = 1
F(N) = F(N - 1) +F(N - 2), 其中 N > 1.
有边界条件
F(0) = 0, F(1) = 1
可以重复调用自身函数
F(N) = F(N - 1) +F(N - 2), 其中 N > 1.
还等什么,递归给冲!等等,每当脑子热的时候我们要冷静一下,题目中的 n 最大可以取100,这递归起来有点可怕了。
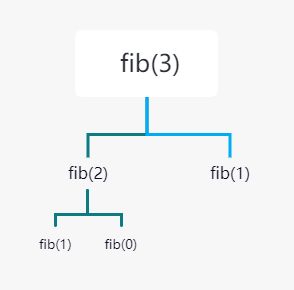
以n=3为例,可以把递归的过程表示成类似二叉树,需要遍历所有分支才能计算出结果。
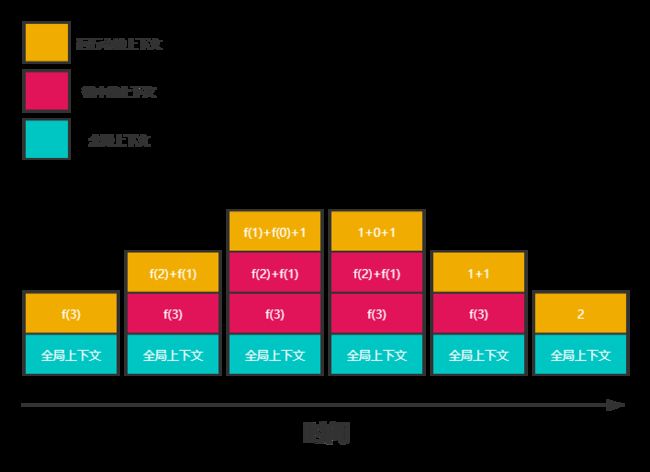
我们都知道JS的执行上下文是存在栈里的,那么内存的使用情况如下:
品红色的框表示正在函数调用栈中的执行上下文,只有在相应的函数执行完并返回时才会被垃圾回收。
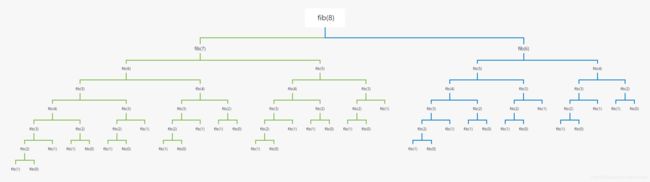
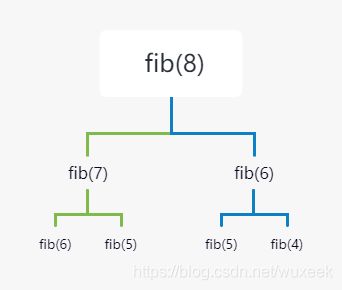
n=3时看起来并没有占用多少内存,但是我们来看看n=8的模拟递归过程的二叉树。
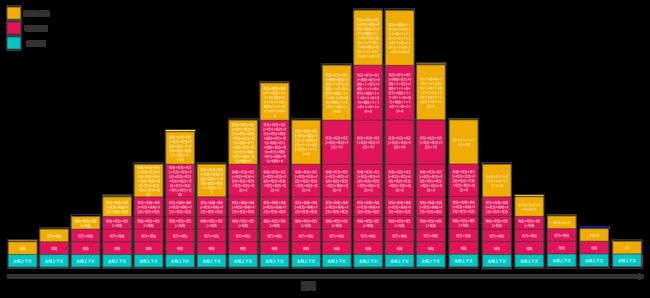
然后来感受下内存使用。
如果n=100呢,可以预见,计算过程会占用太久内存和cpu。为什么会这样呢?归根结底,递归进行了太多次重复运算。
我们把n=8的模拟二叉树简化下。
左边分支中计算了fib(6)和fib(5),右边分支又计算了f(6)和f(5),实际整个递归过程中,大量的都是重复运算。
递归运算会占用太久的内存和cpu,我们必须减少重复的运算。怎么办呢?回归本初,如果没有计算机,你会怎么计算斐波那契数呢?
- f(0) = 0
- f(1) = 1
- f(2) = f(0) + f(1) = 1
- f(3) = f(2) + f(1) = 2
- …
- f(100) = f(99) + f(98)
不就是从小到大,一个个加上去吗,这也是我们这道题的核心思想:“从下往上计算”。你可能会说这有点笨,你也算不过来,实际上比起递归方法计算万亿次,计算100次的工作量不够计算机塞牙缝的。
三、小马甲题解
首先,从下往上算,那我们应该初始化“下”的值。
已知斐波那契数的定义为:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) +F(N - 2), 其中 N > 1.
根据斐波那契数的定义:
F(0) = 0, F(1) = 1
不妨变量a初始化为0,变量b初始化为1。
const fib = function(){
let a = 0,
b = 1;
}
根据递推公式
F(N) = F(N - 1) +F(N - 2), 其中 N > 1.
不妨给a、b换个名字,容易理解
const fib = function(n){
let twoFront = 0, // 隔两位的斐波那契数
oneFront = 1; // 隔一位的斐波那契数
fibN; // n对应的斐波那契数
}
接着,从下往上的过程,实际上是索引规律递增过程,可以用循环来解决。
const fib = function(n){
let twoFront = 0, // 隔两位的斐波那契数
oneFront = 1; // 隔一位的斐波那契数
fibN; // n对应的斐波那契数
for(let i=2; i<=n; i++){
// 计算过程
}
}
计算过程依据斐波那契数的定义
- 已知第一二个的数,计算出第三个数
- 已知第二三个的数,计算出第四个数
- 已知第n-2、n-1个数,计算出第n个数
const fib = function(n){
let twoFront = 0, // 隔两位的斐波那契数
oneFront = 1; // 隔一位的斐波那契数
fibN; // n对应的斐波那契数
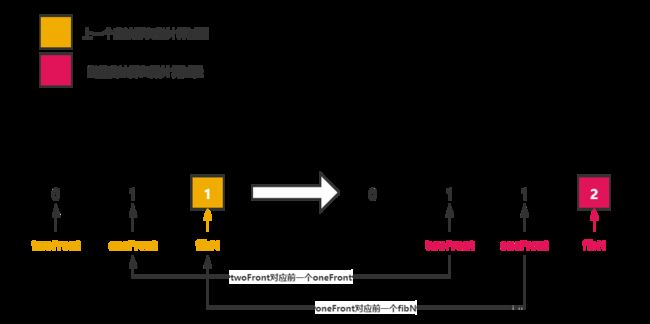
for(let i=2; i<=n; i++){
fibN = twoFront + oneFront; // i对应斐波那契数
twoFront = oneFront; // i+1隔两位的斐波那契数
oneFront = fibN; // i+1隔一位的斐波那契数
}
}
最后,我们不能忘了边界条件的判断,以及对值取模(n比较大时对应的斐波那契数很大,超过16位时可能存储的值不精确)
const fib = function(n){
// let twoFront = 0, // 隔两位的斐波那契数
// oneFront = 1; // 隔一位的斐波那契数
// fibN; // n对应的斐波那契数
if(n===0){
return 0;
}else if(n===1){
return 1;
}
// for(let i=2; i<=n; i++){
fibN = (twoFront + oneFront) % (1e9+7); // i对应斐波那契数
// twoFront = oneFront; // i+1隔两位的斐波那契数
// oneFront = fibN; // i+1隔一位的斐波那契数
// }
// return fibN;
}
我们的最终代码是这样的。
const fib = function(n){
let twoFront = 0, // 隔两位的斐波那契数
oneFront = 1; // 隔一位的斐波那契数
fibN; // n对应的斐波那契数
if(n===0){
return 0;
}else if(n===1){
return 1;
}
for(let i=2; i<=n; i++){
fibN = (twoFront + oneFront) % (1e9+7); // i对应斐波那契数
twoFront = oneFront; // i+1隔两位的斐波那契数
oneFront = fibN; // i+1隔一位的斐波那契数
}
return fibN;
}
四、总结
斐波那契数列是我们很熟悉的东西,本文先从常规的递归思路开始分析,解释了递归方法导致内存使用超时的原因,进而回归“从下往上”计算的思路,大大降低了计算机的工作量。从下往上只需要我们通过一个循环,再设置终止条件即可计算出最终的斐波那契数。值得注意的是:n很大时,对应的斐波那契数会很大,保存的时候可以取模处理。
基础知识关键字:递归、循环、斐波那契数列
上一篇涨薪知识点传送门:剑指Offer面试题:09 用两个栈实现队列