三、Python3实战
1、数据准备
数据集已经为大家准备好,下载地址:数据集下载
这就是一个简单的数据集,没什么实际意义。让我们先从这个简单的数据集开始学习。先看下数据集有哪些数据:
这个数据有两维特征,因此可以将数据在一个二维平面上展示出来。我们可以将第一列数据(X1)看作x轴上的值,第二列数据(X2)看作y轴上的值。而最后一列数据即为分类标签。根据标签的不同,对这些点进行分类。
那么,先让我们编写代码,看下数据集的分布情况:
# -*- coding:UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:加载数据
"""
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
"""
函数说明:绘制数据集
"""
def plotDataSet():
dataMat, labelMat = loadDataSet() #加载数据集
dataArr = np.array(dataMat) #转换成numpy的array数组
n = np.shape(dataMat)[0] #数据个数
xcord1 = []; ycord1 = [] #正样本
xcord2 = []; ycord2 = [] #负样本
for i in range(n): #根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1为正样本
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5) #绘制负样本
plt.title('DataSet') #绘制title
plt.xlabel('x'); plt.ylabel('y') #绘制label
plt.show() #显示
if __name__ == '__main__':
plotDataSet()
运行结果如下:
从上图可以看出数据的分布情况。假设Sigmoid函数的输入记为z,那么z=w0x0 + w1x1 + w2x2,即可将数据分割开。其中,x0为全是1的向量,x1为数据集的第一列数据,x2为数据集的第二列数据。另z=0,则0=w0 + w1x1 + w2x2。横坐标为x1,纵坐标为x2。这个方程未知的参数为w0,w1,w2,也就是我们需要求的回归系数(最优参数)。
2、训练算法
在编写代码之前,让我们回顾下梯度上升迭代公式:
根据矢量化的公式,编写代码如下:
# -*- coding:UTF-8 -*-
import numpy as np
"""
函数说明:加载数据
"""
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
"""
函数说明:sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))、
"""
函数说明:梯度上升算法
"""
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #将矩阵转换为数组,返回权重数组
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
print(gradAscent(dataMat, labelMat))
运行结果如图所示:
可以看出,我们已经求解出回归系数[w0,w1,w2]。
通过求解出的参数,我们就可以确定不同类别数据之间的分隔线,画出决策边界。
3、绘制决策边界
我们已经解出了一组回归系数,它确定了不同类别数据之间的分隔线。现在开始绘制这个分隔线,编写代码如下:
# -*- coding:UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np
"""
函数说明:加载数据
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(int(lineArr[2])) #添加标签
fr.close() #关闭文件
return dataMat, labelMat #返回
"""
函数说明:sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
"""
函数说明:梯度上升算法
Parameters:
dataMatIn - 数据集
classLabels - 数据标签
Returns:
weights.getA() - 求得的权重数组(最优参数)
"""
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #将矩阵转换为数组,返回权重数组
"""
函数说明:绘制数据集
Parameters:
weights - 权重参数数组
"""
def plotBestFit(weights):
dataMat, labelMat = loadDataSet() #加载数据集
dataArr = np.array(dataMat) #转换成numpy的array数组
n = np.shape(dataMat)[0] #数据个数
xcord1 = []; ycord1 = [] #正样本
xcord2 = []; ycord2 = [] #负样本
for i in range(n): #根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1为正样本
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5) #绘制负样本
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit') #绘制title
plt.xlabel('X1'); plt.ylabel('X2') #绘制label
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights = gradAscent(dataMat, labelMat)
plotBestFit(weights)
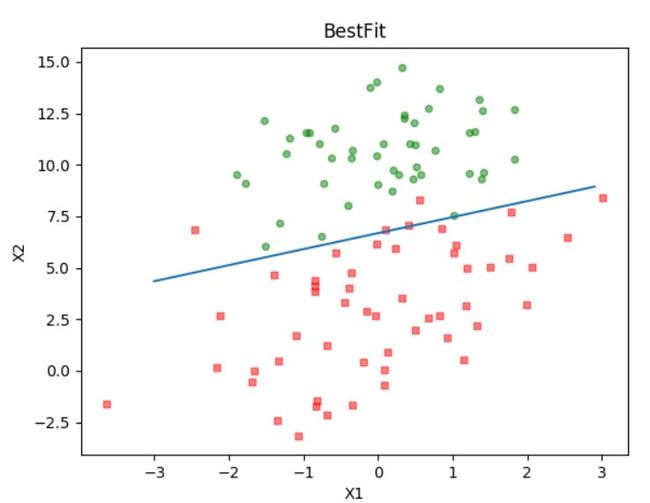
运行结果如下:
这个分类结果相当不错,从上图可以看出,只分错了几个点而已。但是,尽管例子简单切数据集很小,但是这个方法却需要大量的计算(300次乘法)。因此下篇文章将对改算法稍作改进,从而减少计算量,使其可以应用于大数据集上。免费视频教程:www.mlxs.top