红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
性质
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶子节点(NIL)是黑色。 (注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!)
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的HashMap和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
旋转
为了保证上面的5点特性,所以在新插入或删除的节点的时候,我们为了保证上述特性需要对树进行旋转。下图的正方形A、B和C代表一个不会破坏红黑树结构的部分,可能是节点,或者是一个子树,也有可能是NULL。这个部分会由于旋转而连接到其他的节点后面,我们可以理解成由于重力原因它掉到了下面的节点上。
单旋转变换
当两个连续的红色节点都是左叶子节点,并且父节点的兄弟节点是黑色的时候需要进行右旋操作。
如图,X和P都是左叶子节点,并且X的父节点P的兄弟结点S是黑色。
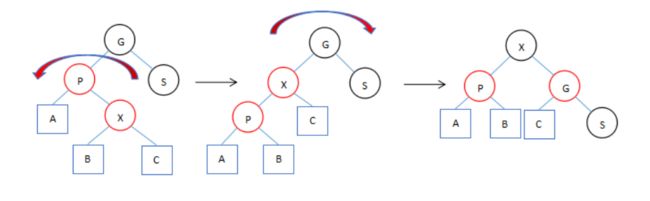
双旋转变换
当两个连续的红色节,点父子节点分别是左右叶子节点,父节点的兄弟节点是黑色的时候需要进行两次旋操作,先对P节点左旋,旋转后就是第一种情况了,再对G节点右旋。如图:
节点变色
当遇到两个子几点都为红色的话执行颜色变换,因为插入 是红色的会产生冲突。如果根节点两边的子节点都是红色,两个叶子节点变成黑色,根节点变成红色,然后再将根节点变成黑色。
HashMap内红黑树的实现
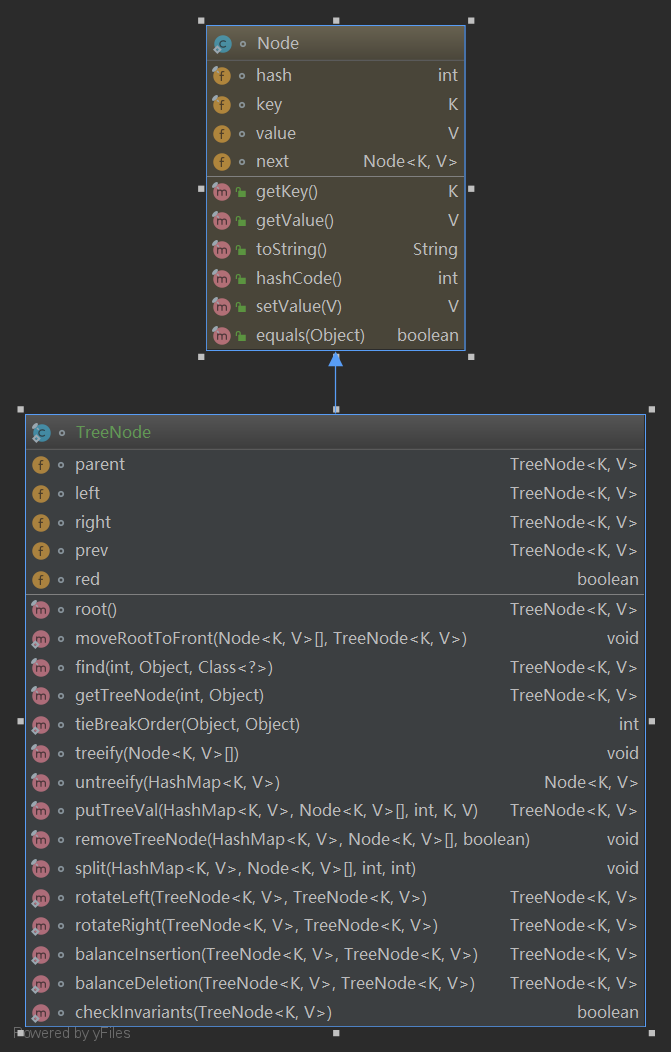
HashMap内所有对红黑树的操作都被封装到了TreeNode这个类里面。如图:
TreeNode里面包含了基本怎删查操作,还有旋转。
putTreeVal() 新增节点
final TreeNode putTreeVal(HashMap map, Node[] tab,
int h, K k, V v) {
Class kc = null;
boolean searched = false;
// 找到根节点
TreeNode root = (parent != null) ? root() : this;
for (TreeNode p = root; ; ) {
// dir 表示两个key的比较结果,ph表示p节点的hash值
int dir, ph;
K pk;
if ((ph = p.hash) > h)
// 父节点的hash值大于新节点hash值
dir = -1;
else if (ph < h)
// 父节点的hash值小于新节点hash值
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
// 表示key完全相同
return p;
else if ((kc == null &&
// 判断对key是否实现Comparable接口
(kc = comparableClassFor(k)) == null) ||
// 使用Comparable来比较父节点和新节点的key值大小
(dir = compareComparables(kc, k, pk)) == 0) {
// 这个查找只会执行一次
if (!searched) {
TreeNode q, ch;
searched = true;
// 从p的左子树找到对应key的节点
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
// 从p的右子树找到对应key的节点
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
//表示key完全相同的节点
return q;
}
// 使用默认比较器比较两个key的大小
dir = tieBreakOrder(k, pk);
}
TreeNode xp = p;
// 自旋找出新节点的父节点
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node xpn = xp.next;
TreeNode x = map.newTreeNode(h, k, v, xpn);
// 将新节点放到对应的叶子节点位置
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode) xpn).prev = x;
// 调整树的平衡
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
balanceInsertion()方法
每次新增一个节点默认是红色节点,所以每次新增节点过后都我们可以保证特性5不会被破坏,但有可能会破坏特性4,所以我们需要调用balanceInsertion方法在新增一个节点X后,调用旋转方法来保证红黑树特性,代码如下:
static TreeNode balanceInsertion(TreeNode root, TreeNode x) {
// 所有新插入的节点都是红色
x.red = true;
// xp:x parent,代表x的父节点。
// xpp:x parent parent,代表x的祖父节点
// xppl:x parent parent left,代表x的祖父的左节点。
// xppr:x parent parent right,代表x的祖父的右节点。
for (TreeNode xp, xpp, xppl, xppr; ; ) {
// 如果父节点为NULL说明只有一个节点,说明它就是根节点(第一个节点)直接将X节点染黑就行
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 不是根节点
// 如果父节点是黑色,那么红色节点可以直接加在后面,这样对树结构不会有影响,直接返回
// 祖父节点为NULL表式父节点为根节点,根节点必须是黑色可以直接添加红色节点
else if (!xp.red || (xpp = xp.parent) == null)
return root;
/**到了这里说明X的父节点是红色并且它是有祖父节点的*/
// 父节点是祖父节点的左叶子结点
if (xp == (xppl = xpp.left)) {
// 父节点的右边兄弟是红色,将父节点和父节点的兄弟节点染黑,将祖父节点染红。这个其实是上面的旋转3
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 父节点的兄弟节点为null或者为黑色,这个其实是上面的旋转2,先左旋再右旋
else {
// X是否是右子节点,此时结构是xpp左->xp右->x,这种
if (x == xp.right) {
// 左旋转
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 针对本身就是xpp左->xp左->x的结构或者由于上面的旋转造成的这种结构进行一次旋转。这个其实是上面的旋转1
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
// 右旋转
root = rotateRight(root, xpp);
}
}
}
}
// 父节点是祖父节点的右叶子结点
else {
// 父节点的左边兄弟是红色
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
} else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
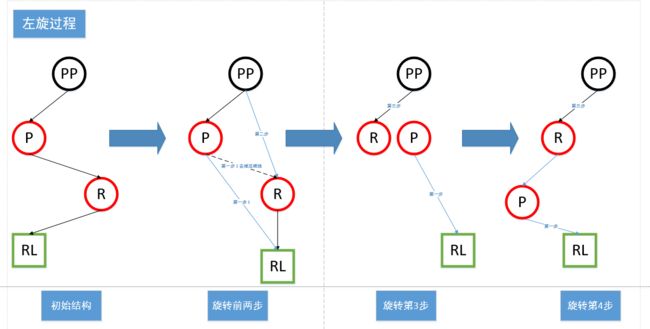
rotateLeft() 左旋
static TreeNode rotateLeft(TreeNode root,
TreeNode p) {
// r:right,右节点。
// pp:parent parent,父节点的父节点。
// rl:right left,右节点的左节点。
TreeNode r, pp, rl;
if (p != null && (r = p.right) != null) {
// 第一步
if ((rl = p.right = r.left) != null)
rl.parent = p;
// 第二步
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
// 第三部
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
// 第四步
r.left = p;
p.parent = r;
}
return root;
}
rotateRight() 右旋
balanceInsertion() {
// ...
if (xp != null) {
xp.red = false;
if (xpp != null)
{
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
// ...
}
static TreeNode rotateRight(TreeNode root,
TreeNode p) {
// l:left,左节点。
// pp:parent parent,父节点的父节点。
// lr:left right,左节点的右节点。
TreeNode l, pp, lr;
if (p != null && (l = p.left) != null) {
// 第一步
if ((lr = p.left = l.right) != null)
lr.parent = p;
// 第二步
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
// 第三步
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
// 第四步
l.right = p;
p.parent = l;
}
return root;
}
节点变色
balanceInsertion() {
// ...
for (TreeNode xp, xpp, xppl, xppr; ; ) {
// 如果父节点为NULL说明它就是根节点(第一个节点)直接将X节点染黑就行
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 不是根节点
// 如果父节点是黑色,那么红色节点可以直接加在后面,这样对树结构不会有影响,直接返回
// 祖父节点为NULL表式父节点为根节点,根节点必须是黑色可以直接添加红色节点
else if (!xp.red || (xpp = xp.parent) == null)
return root;
/**到了这里说明X的父节点是红色并且它是有祖父节点的*/
// 父节点是祖父节点的左叶子结点
if (xp == (xppl = xpp.left)) {
// 父节点的右边兄弟是红色,将父节点和父节点的兄弟节点染黑,将祖父节点染红
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// ...
}
如果P是根节点,那么在下一次循环的时候会将P染成黑色。
参考
https://www.cnblogs.com/finite/p/8251587.html
https://www.cnblogs.com/xuxinstyle/p/9556998.html
https://www.bilibili.com/video/av23890827/
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
layering-cache
为监控而生的多级缓存框架 layering-cache这是我开源的一个多级缓存框架的实现,如果有兴趣可以看一下