一、哈夫曼树
具有n个权值的n个叶子结点,构造出一个二叉树,使得该树的带权路径长度(WPL)最小,则称此二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
注意:哈夫曼树是带权路径长度最短的树,且权值越大的叶子结点离根结点越近。
二、哈夫曼编码
哈夫曼编码是一种编码方式,又称“霍夫曼编码”,其是可变字长的编码(VCL)的一种,是由霍夫曼于1952年提出的一种编码方式,有时被称为最佳编码,一般称为Huffman编码。
那么我们为什么要使用哈夫曼编码进行压缩?
首先原因在于,传统压缩方式中,字符的编码是以等字长的方式进行压缩,相比于哈夫曼编码的可变字长而言压缩率会降低。其次,传统方式中可能会出现某些字符的编码相同,存在二义性,相比于哈夫曼编码的唯一性。可以大大提高正确性。
2.1 如何得到哈夫曼编码
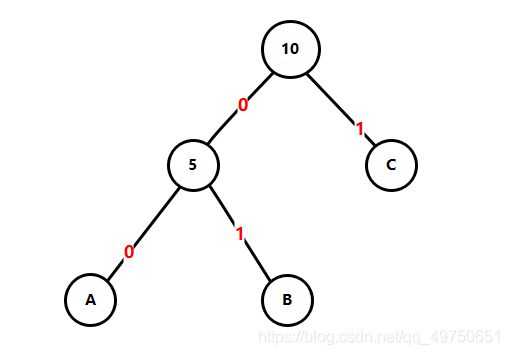
通过已经构造的哈夫曼树,结点左分支记为二进制数“0”,结点右分支记为二进制数“1”。从根结点向下到该叶子结点路途经过的数字拼接成为的编码即为该字符的哈夫曼编码。现通过以下图例进行演示。
此时各字符对应的哈夫曼编码可表示为:
A:00 B:01 C:1
三、哈夫曼树实现文件压缩基本步骤
3.1 基本实现流程
3.2 使用文件输入流读取需压缩的文件,并判断该文件是否存在
存在后执行接下来的步骤,不存在提示用户,效果图如下
3.3 读取,统计字符
用户输入正确文件路径且存在时使用文件输入流读取文件,将文件放于一个字符数组中(注意字符数组开辟空间应足够大)。统计出现的字符及其出现的次数。
char ch;
while(feof(fp) == 0){
fscanf(fp,"%c",&ch);
str[ch]++;
}
printf("\n");
for(i = 0; i < 1024; i++){
if(str[i] != 0){
count[n++] = i;
}
}
3.4 构造哈夫曼树
注:由于后续会使用此哈夫曼编码,为了方便获取,这里将求出的哈夫曼编码放置于一个二维数组中。
CreateHT(ht,node);
char strarr[256][256];
int aa,bb;
for(aa=0; aa<256;aa++)
for(bb=0;bb<256;bb++)
strarr[aa][bb]=-1;
for(k = 0;k < node;k++){
huffmanCode(ht,k,strarr[k]);
}
void CreateHT(HTNode *ht, int n){
int i, j, lnode, rnode n1, n2;
for(i = n; i < 2*n-1; i++){
lnode = 65432; rnode = lnode;
n1 = 0; n2 = 0;
for(j = 0; j < i; j++){
if(ht[j].parent == -1){
if(ht[j].weight
3.5 根据构造哈夫曼树得到哈夫曼编码
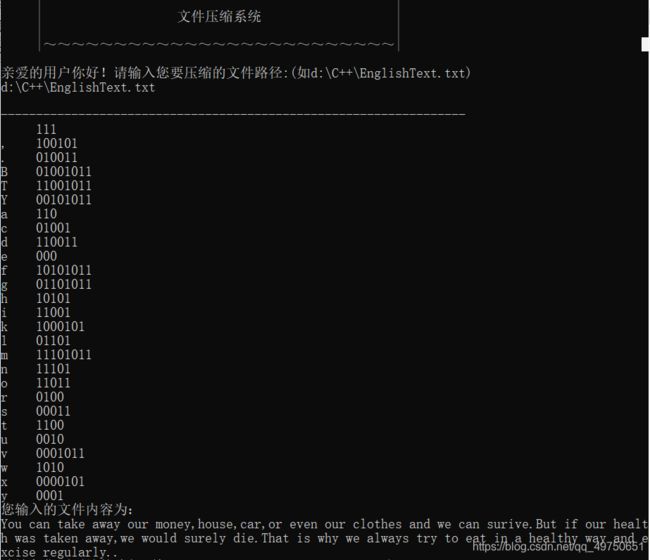
此时我们使用3.3中统计的字符作为叶子结点,其出现次数作为权值,构造哈夫曼树求出哈夫曼编码。下面以此段英文为例,得到每个字符对应哈夫曼编码。
You can take away our money,house,car,or even our clothes and we can surive.But if our health was taken away,we would surely die.That is why we always try to eat in a healthy way and excise regularly..
3.6 替换字符为其哈夫曼编码
用户输入压缩至的文件路径,将替换好的0 1数字字符数组写入该文件。由于C语言没有基于字符串的操做,所以我们替换时只能通过对字符数组进行操作,涉及到了被替换字符串长度与替换字符串长度的问题,以及字符数组的长度是否充足。由于此次替换被替换字符串只是一个字符,且字符数组开辟空间足够大。所以只考虑替换字符串长度,即字符对应哈夫曼编码的长度,在这里使用一个方法来进行替换。
void replace(char oldstr[], char key[], char rep[]){
int oldstrLen, lengthOfKey, lengthOfRep, i, j , flag;
char tmp[1000];
oldstrLen = strlen(oldstr);
lengthOfKey = strlen(key);
lengthOfRep = strlen(rep);
for( i = 0; i <= oldstrLen - lengthOfKey; i++){
flag = 1;
for(j = 0; j < lengthOfKey; j++){
if(oldstr[i + j] != key[j]){
flag = 0;
break;
}
}
if(flag){
strcpy(tmp, oldstr);
strcpy(&tmp[i], rep);
strcpy(&tmp[i + lengthOfRep], &oldstr[i + lengthOfKey]);
strcpy(oldstr, tmp);
i += lengthOfRep - 1;
oldstrLen = strlen(oldstr);
}
}
}
替换完成后的字符数组使用输出流写入用户输入文件路径。
3.7 进制转换
将文件中每八位二进制数转换为十进制数,再转换为其对应的ASCII码值,最后不足八位的二进制数以0补齐,实现文件压缩。
3.7.1 进制转换方法
int retTen(char str[]){
int ten = 0;
int t = 0;
for(t = 0;t < strlen(str);t++){
ten += (str[t]-'0') * pow(2,strlen(str) - t - 1);
}
return ten;
}
3.7.2 实现效果
3.8 计算压缩率
最后为验证是否实现压缩,可通过计算文件压缩率来验证。其中,压缩率=原文件字节大小/压缩后文件大小。
int oldFileSize=getFileSize(path);
int newFileSize=getFileSize(Gopath);
printf("\n");
printf("压缩成功!,文件已压缩至%s\n",Gopath);
printf("该文件压缩率为:%.2lf\n",(double)newFileSize/(double)oldFileSize);
注:注意计算压缩率时的类型转换
到此这篇关于基于C语言利用哈夫曼树实现文件压缩的文章就介绍到这了,更多相关C语言实现文件压缩内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!