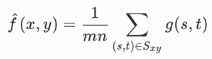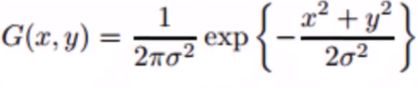OpenCV(十一)图像滤波(平滑处理)(平均、中值、高斯、双边滤波)
目录
一、基础理论
1、图像噪声
1-1、椒盐噪声
1-2、高斯噪声
2、滤波
3、线性滤波
1、概述
2、线性滤波原理:
二、均值滤波(cv::blur())(简单滤波)
1、原理
2、API
三、中值滤波(cv::medianBlur())
1、基础理论
1、作用
2、原理
2、API
3、效果
四、高斯滤波(cv::GaussianBlur())
1、基础理论
作用:
原理:
分布:
过程:
2、API
五、双边滤波(cv::bilateralFilter())
API
总代码
C++:
python:
参考资料
一、基础理论
1、图像噪声
由于图像采集、处理、传输等过程不可避免的会受到噪声的污染,妨碍人们对图像理解及分析处理。常见的图像噪声有高斯噪声、椒盐噪声等。
1-1、椒盐噪声
椒盐噪声也称为脉冲噪声,是图像中经常见到的一种噪声,它是一种随机出现的白点或者黑点,可能是亮的区域有黑色像素或是在暗的区域有白色像素(或是两者皆有)。椒盐噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。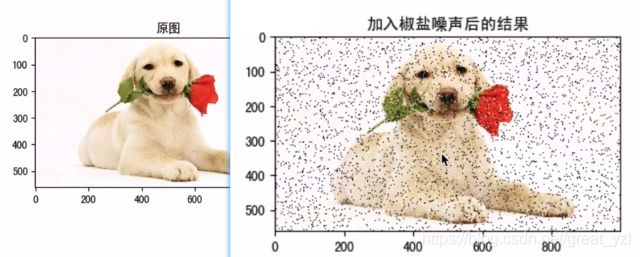
1-2、高斯噪声
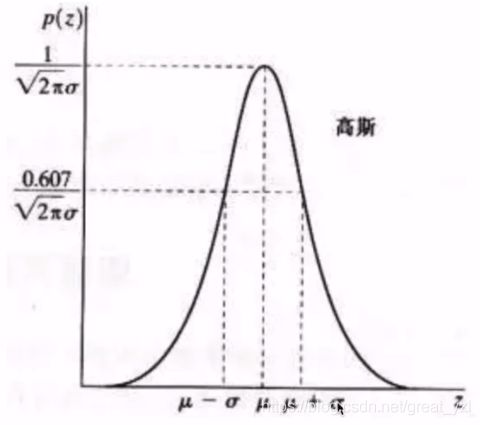
高斯噪声是指噪声密度函数服从高斯分布的一类噪声。由于高斯噪声在空间和频域中数学上的易处理性,这种噪声(也称为正态噪声)模型经常被用于实践中。高斯随机变量z的概率密度函数公式: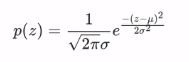
![]()
高斯分布(正太分布):
为了去除噪声,我们引入滤波(平滑)技术:
2、滤波
“平滑”(滤波)通常又称“模糊”,是一种简单常用的图像处理操作。进行平滑处理的原因有很多,但通常是用来去除噪声和相机失真,平滑在按照一定的原理来降低图像分辨率中也有重要应用。
根据空间滤波增强目的可分为:平滑滤波和锐化滤波;
根据空间滤波的特点可分为:线性滤波和非线性滤波。
(1)平滑滤波,能减弱或消除图像中的高频分量,但不影响低频分量。因为高频分量对应图像中的区域边缘等灰度值具有较大、较快变化的部分,平滑滤波将这些分量绿区可减少局部灰度的起伏,使图像变得比较平滑。实际应用中,平滑滤波即可以用来消除噪声,又可以用在提取较大的目标前过滤去除较小的细节或将目标内的小间断连接起来。
(2)锐化滤波,能减弱或消除图像中的低频分量,但不影响高频分量。因为低频分量对应图像中灰度值缓慢变化的区域,因而与图像的整体特性如整体对比度和平均灰度值等有关。锐化滤波将这些分量滤去可使图像反差增加,边缘明显。实际应用中,锐化滤波可用于增强图像中被模糊的细节或景物的边缘。
(1)线性滤波:运算只是对各像素灰度值进行简单处理(如乘一个权值)最后求和。
(2)非线性滤波:如果对像素灰度值的复杂运算,而不是最后求和的简单运算。
3、线性滤波
1、概述
常见的线性滤波器:
(1)低通滤波器:允许低频率通过;
(2)高通滤波器:允许高频率通过;
(3)带通滤波器 :允许一定区域的频率通过;
(4)带阻滤波器 :阻止一定范围内的频率并且允许其他频率通过;
(5)全通滤波器 :允许所有频率通过,仅仅改变相位;
(6)陷波滤波器(Band stop filter):阻止一个狭窄频率范围通过的特殊带阻滤波器。
方框滤波–> boxblur函数来实现 –> 线性滤波
均值滤波–> blur函数 –> 线性滤波
高斯滤波–> GaussianBlur函数 –> 线性滤波
中值滤波–> medianBlur函数 –> 非线性滤波
双边滤波–> bilateralFilter函数 –> 非线性滤波
2、线性滤波原理:
线性邻域滤波是一种常用的邻域算子。邻域算子(局部算子)是利用给定像素周围的像素值的决定此像素的最终输出值的一种算子。下面这个图解可以很好的说明这个过程:
邻域算子(局部算子)是利用给定像素周围的像素值的决定此像素的最终输出值的一种算子。而线性邻域滤波是一种常用的邻域算子,像素的输出值取决于输入像素的加权和,具体过程如下图。
假设有6x6的图像像素点矩阵。卷积过程:6x6上面是个3x3的窗口,从左向右,从上向下移动,黄色的每个像个像素点值之和取平均值赋给中心红色像素作为它卷积处理之后新的像素值。每次移动一个像素格。
平滑(smoothing)/模糊(bluring)的数学理论幕后黑手——卷积:![]()
线性滤波处理的输出像素值g(i,j)也就是上面的红心的值(锚点),是输入图像f(i+k,j+l)的加权和。h(k,l)是核,也是窗口大小;
二、均值滤波(cv::blur())(简单滤波)
1、原理
图像的简单平滑就是均值滤波,对图像中一定邻域内的像素灰度值求平均值,将平均的结果作为中心像素的灰度保存在结果图中。(在多通道图像中,每个通道需要分别计算。)
![]()
2、API
void cv::blur(
cv::InputArray src, // 输入图像
cv::OutputArray dst, // 输出图像
cv::Size ksize, // 核大小
cv::Point anchor = cv::Point(-1,-1), // 锚点位置
int borderType = cv::BORDER_DEFAULT // 边界处理方法
);C++
blur(src, dst, Size(9, 9), Point(-1, -1)); //均值滤波python:
ave = cv2.blur(img, (9, 9)) #均值滤波三、中值滤波(cv::medianBlur())
1、基础理论
1、作用
适合去除椒盐噪声。
2、原理
cv::medianBlur()即通常所说的中值滤波,其主要思想是,对中心像素矩形邻域取中值来替代中心像素。平滑效果如下:
![]()
2、API
void cv::medianBlur(
cv::InputArray src, // 输入图像
cv::OutputArray dst, // 输出图像
cv::Size ksize // 核大小
);C++:
medianBlur(src, dst, 9); //中值滤波python:
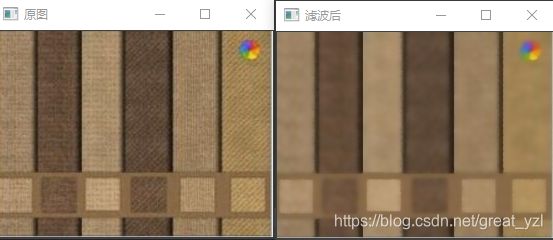
med = cv2.medianBlur(img, 3) # 均值滤波3、效果
四、高斯滤波(cv::GaussianBlur())
1、基础理论
作用:
适合处理高斯噪声。(往中心集中的那种)
原理:
让临近像素具有更高的权重,起到模糊的效果 。
cv::GaussianBlur()即高斯滤波,是最常用的一种滤波方式。其主要思想是,使用高斯核与输入图像中的每个点作卷积运算,然后对卷积结果进行求和,从而得到输出图像。
在图像高斯平滑中,对图像进行平均时,不同位置的像素被赋予了不同的权重。高斯平滑与简单平滑不同,它在对邻域内像素进行平均时,给予不同位置的像素不同的权值。
分布:
公式:
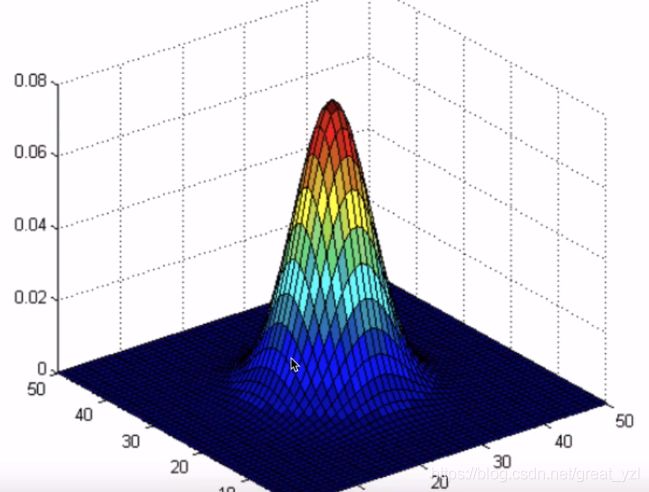
分布:高斯分布(正态分布)
正态分布(高斯分布)是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。计算平滑结果时,只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。
过程:
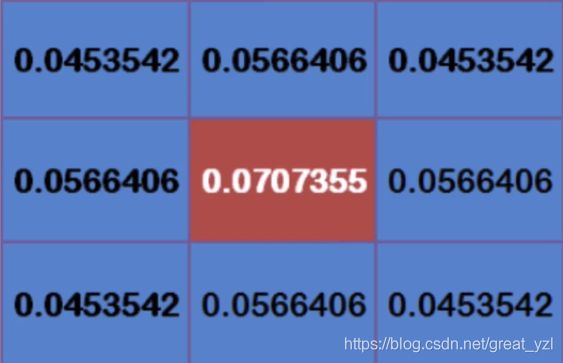
1、得到权重矩阵
(1)得到权重
这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。
(2)归一化权重(权重矩阵)2、对实际像素处理(乘权重矩阵)
(1)像素点
(2)乘权重矩阵
(3)得到最终像素
2、API
void cv::GaussianBlur(
cv::InputArray src, // 输入图像
cv::OutputArray dst, // 输出图像
cv::Size ksize, // 核大小
double sigmaX, // x方向高斯半宽
double sigmaY = 0.0, // y方向高斯半宽
int borderType = cv::BORDER_DEFAULT // 边界处理方法
);C++:
GaussianBlur(src, dst, Size(9, 9), 0); //高斯滤波python:
Gausi = cv2.GaussianBlur(img, (3,3), 1) # 均值滤波
# 往X方向偏移量五、双边滤波(cv::bilateralFilter())
API
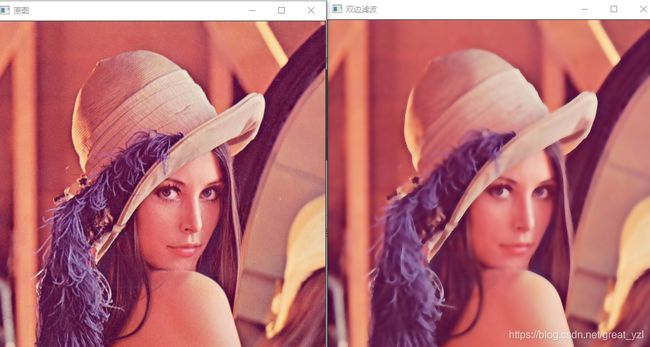
cv::bilateralFilter(),即双边滤波,是一种可以保持图像边缘的平滑方法。和高斯滤波类似,双边滤波也是通过计算中像素和邻域像素的加权平均所实现的,只是其权值由两部分组成。其中,第一部分与高斯平滑的权值相同;第二部分也是高斯权值,但是该权值并不是基于中心像素的空间距离,而是基于和中心像素点的灰度值的差异。
cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace, dst=None, borderType=None)
三个重要参数:
第一个参数d是滤波过程中的像素邻域直径;
第二个参数是用于颜色域高斯核的参数,称作sigmaColor,和高斯滤波中的sigma参数类似;
第三个参数是空间域中的高斯核宽度,称作sigmaSpace。
C++:
bilateralFilter(src, dst, 9, 75, 75); //双边滤波python:
Bila = cv2.bilateralFilter(img, 0, 100, 15) # 双边滤波
# 像素直径 颜色空间过滤 坐标空间过滤
#颜色空间过滤、坐标空间过滤越大,滤波效果越好总代码
C++:
//图像平滑(滤波)(均值滤波、中值滤波、高斯滤波、双边滤波)
#include
using namespace cv;
Mat src, dst;
//图像初始化
void Image_Init()
{
src = imread("Resource/3.jpg");
dst = Mat::zeros(src.size(), src.type());
if (src.empty())
{
printf("图像加载失败");
exit(0);
}
}
int main()
{
Image_Init();
//均值滤波
blur(src, dst, Size(5, 5), Point(-1, -1)); //均值滤波
GaussianBlur(src, dst, Size(7, 7), 0); //高斯滤波
medianBlur(src, dst, 5); //中值滤波
bilateralFilter(src, dst, 9, 75, 75); //双边滤波
imshow("原图", src);
imshow("滤波后", dst);
waitKey(0);
}
python:
# 图像滤波(平滑处理)
import cv2
# 均值滤波
def Average():
ave = cv2.blur(img, (3, 3)) #均值滤波
cv2.imshow('average blur', ave)
# 中值滤波
def MedianBlur():
med = cv2.medianBlur(img, 3) # 中值滤波
cv2.imshow('medianBlur', med)
# 高斯滤波
def GaussianBlur():
Gausi = cv2.GaussianBlur(img, (3,3), 1) # 高斯滤波
# 往X方向偏移量
cv2.imshow('GaussianBlur', Gausi)
# 双边滤波
def BilateralFilter():
Bila = cv2.bilateralFilter(img, 0, 100, 15) # 双边滤波
# 像素直径 颜色空间过滤 坐标空间过滤
#颜色空间过滤、坐标空间过滤越大,滤波效果越好
cv2.imshow('bilateralFilter', Bila)
if __name__ == '__main__':
img = cv2.imread('Resource/gaosi.jpg')
cv2.imshow('img', img)
Average() #均值滤波
MedianBlur() #中值滤波
GaussianBlur() #高斯滤波
BilateralFilter() #双边滤波
cv2.waitKey(0)参考资料
https://blog.csdn.net/zhu_hongji/article/details/81479571
https://blog.csdn.net/guduruyu/article/details/68064185?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162875288016780265475806%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=162875288016780265475806&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-5-68064185.first_rank_v2_pc_rank_v29&utm_term=%E5%B9%B3%E6%BB%91%E5%A4%84%E7%90%86&spm=1018.2226.3001.4187
https://blog.csdn.net/dongyu_1989/article/details/78310583
https://blog.csdn.net/zaishuiyifangxym/article/details/89788020?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162875251616780366527440%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=162875251616780366527440&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-2-89788020.first_rank_v2_pc_rank_v29&utm_term=%E9%AB%98%E6%96%AF%E6%BB%A4%E6%B3%A2&spm=1018.2226.3001.4187
https://www.bilibili.com/video/BV1Fo4y1d7JL?p=24&spm_id_from=pageDriver
http://woshicver.com/FifthSection/4_4_%E5%9B%BE%E5%83%8F%E5%B9%B3%E6%BB%91/
https://iamarookie.blog.csdn.net/article/details/118873000