2021.7.19模拟赛C组总结

2021.7.19模拟赛C组总结

这次的题做的不怎么样，刚学的exgcd居然忘了…

题解

T1

题目描述：

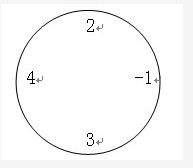
​ 丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单，但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的，在你面前有一圈整数（一共n个），你要按顺序将其分为m个部分，各部分内的数字相加，相加所得的m个结果对10取模后再相乘，最终得到一个数k。游戏的要求是使你所得的k最大或者最小。

​ 例如，对于下面这圈数字（n=4，m=2）：

​ 当要求最小值时，((2-1) mod 10)×((4+3) mod 10)=1×7=7，要求最大值时，为((2+4+3) mod 10)×(-1 mod 10)=9×9=81。特别值得注意的是，无论是负数还是正数，对10取模的结果均为非负值。

​ 丁丁请你编写程序帮他赢得这个游戏。

比赛思路：

​ 想过队列，贪心之类的解法，但是都不行，没想到其他的方法，喜提0分

正解：

​ 用区间动态规划，由于这个序列会形成一个环，所以可以将用于存储原序列的a数组进行预处理，使得a[i]=a[i+n],即将数组a[1...n]复制到a[n+1...n×2]中，便于使用数组模拟环，再预处理一个前缀和数组sum[1...n×2]，设f1[i][j][k]表示在原序列a中区间[i,j]被分为k个部分时，所能求得的最小值，f2[i][j][k]则表示最大值，动态转移方程如下：
$$f1i,j,k=min(f{1}_{i,j,k},f{1}_{i,p,k-1}\times (su{m}_j-su{m}_p)mod10)$$

$$f2i,j,k=max(f{2}_{i,j,k},f{2}_{i,p,k-1}\times (su{m}_j-su{m}_p)mod10)$$

最后用变量存储最大值与最小值即可

Code：

#include
#define in scanf
#define out printf
#define rint register int
using namespace std;
const int inf=2e9;
int n,m,a[101],sum[101];
int f1[101][101][101],f2[101][101][101];
int md(int x)
	{
     return((x%10+10)%10);}
int main() {
     
	in("%d%d",&n,&m);
	for(rint i=1;i<=n;i++) {
     
		in("%d",&a[i]);
		a[i+n]=a[i];//处理环
		sum[i]=sum[i-1]+a[i];//前缀和数组
	}
	for(rint i=n+1;i<=n*2;i++) sum[i]=sum[i-1]+a[i];
	int maxn=-inf;
	int minn=inf;
	for(rint i=1;i<=n;i++) {
     
		for(rint j=1;j<=2*n;j++)
			for(rint k=1;k<=2*n;k++) {
     
				f1[i][j][k]=inf;
				f2[i][j][k]=-inf;
			}
			for(rint j=i;j<=i+n-1;j++) {
     
				f1[i][j][1]=md(sum[j]-sum[i-1]);
				f2[i][j][1]=md(sum[j]-sum[i-1]);
			}
			for(rint j=i;j<=i+n-1;j++)
				for(rint k=2;k<=min(m,j-i+1);k++)
					for(rint p=k+i-2;p<=j-1;p++) {
     
						f1[i][j][k]=min(f1[i][j][k],f1[i][p][k-1]*md(sum[j]-sum[p]));
						f2[i][j][k]=max(f2[i][j][k],f2[i][p][k-1]*md(sum[j]-sum[p]));//DP
					}
		minn=min(minn,f1[i][i+n-1][m]);
		maxn=max(maxn,f2[i][i+n-1][m]);
	}
	out("%d\n%d",minn,maxn);
	return 0;
}

显然，f1和f2数组的第一维是不影响结果的，可以直接去掉，优化空间复杂度

#include
#define in scanf
#define out printf
#define rint register int
using namespace std;
const int inf=2e9;
int n,m,a[101],sum[101];
int f1[101][101],f2[101][101];
int md(int x)
	{
     return((x%10+10)%10);}
int main() {
     
	in("%d%d",&n,&m);
	for(rint i=1;i<=n;i++) {
     
		in("%d",&a[i]);
		a[i+n]=a[i];
		sum[i]=sum[i-1]+a[i];
	}
	for(rint i=n+1;i<=n*2;i++) sum[i]=sum[i-1]+a[i];
	int maxn=-inf;
	int minn=inf;
	for(rint i=1;i<=n;i++) {
     
		for(rint j=1;j<=2*n;j++)
			for(rint k=1;k<=2*n;k++) {
     
				f1[j][k]=inf;
				f2[j][k]=-inf;
			}
			for(rint j=i;j<=i+n-1;j++) {
     
				f1[j][1]=md(sum[j]-sum[i-1]);
				f2[j][1]=md(sum[j]-sum[i-1]);
			}
			for(rint j=i;j<=i+n-1;j++)
				for(rint k=2;k<=min(m,j-i+1);k++)
					for(rint p=k+i-2;p<=j-1;p++) {
     
						f1[j][k]=min(f1[j][k],f1[p][k-1]*md(sum[j]-sum[p]));
						f2[j][k]=max(f2[j][k],f2[p][k-1]*md(sum[j]-sum[p]));
					}
		minn=min(minn,f1[i+n-1][m]);
		maxn=max(maxn,f2[i+n-1][m]);
	}
	out("%d\n%d",minn,maxn);
	return 0;
}

T2

题目描述：

​ Beny 想要用蛋糕填饱肚子。Beny 一共想吃体积为 c 的蛋糕，他发现有两种蛋糕可以吃，一种体积为 a，一种体积为 b，但两种蛋糕各有特色。Beny 想知道他一共有多少种不同吃法， 使得他恰好可以填饱肚子。

比赛思路：

​ 知道用exgcd，但是基础不牢，不会实现，打了暴力得30分

正解：

​ 用exgcd求方程ax+by=c整数解中y最大的一组解，解的组数=最大的y/a+1

Code:

注：要用long long 数据类型

#include
#define in scanf
#define out printf
#define lon long long
using namespace std;
lon gcd(lon a,lon b)
	{
     return a%b==0?b:gcd(b,a%b);}
void exgcd(lon a,lon b,lon&x,lon&y) {
     
	if(b==0) {
     
		x=1; y=0;
		return;
	}
	exgcd(b,a%b,y,x);
	y-=a/b*x;
	return;
}
signed main() {
     
	lon t,a,b,x,y,c,k;
	in("%lld",&t);
	for(register int i=1;i<=t;i++) {
     
		in("%lld%lld%lld",&a,&b,&c);
		k=gcd(a,b);
		if(c%k!=0) {
     
			out("0\n");
			continue;
		}
		exgcd(a,b,x,y);
		a/=k; b/=k; c/=k;
		x=((x%b+b)%b*(c%b)%b+b)%b;
		y=(c-a*x)/b;
		if(y<0) {
     
			out("0\n");
			continue;
		}
		else out("%lld\n",y/a+1);
	}
	return 0;
}

T3

题目描述：

​ 恶魔猎手尤迫安野心勃勃.他背叛了暗夜精灵，率深藏在海底的那加企图叛变：守望者在与尤迪安的交锋中遭遇了围杀.被困在一个荒芜的大岛上。为了杀死守望者，尤迪安开始对这个荒岛施咒，这座岛很快就会沉下去，到那时，岛上的所有人都会遇难：守望者的跑步速度，为17m/s， 以这样的速度是无法逃离荒岛的。庆幸的是守望者拥有闪烁法术，可在1s内移动60m，不过每次使用闪烁法术都会消耗魔法值10点。守望者的魔法值恢复的速度为4点/s，只有处在原地休息状态时才能恢复。

​ 现在已知守望者的魔法初值M，他所在的初始位置与岛的出口之间的距离S，岛沉没的时间T。你的任务是写一个程序帮助守望者计算如何在最短的时间内逃离荒岛，若不能逃出，则输出守望者在剩下的时间内能走的最远距离。注意:守望者跑步、闪烁或休息活动均以秒(s)为单位。且每次活动的持续时间为整数秒。距离的单位为米(m)。

比赛思路：

​ 想到了贪心正解，结果不知为什么WA了50分，赛后按原先的想法重新打了一遍就AC了，可能是细节没弄好

正解：

​ 贪心，先用已有的魔法值用完法术，再枚举时间 i(from 1 to T)，判断在第 i 秒时跑和停哪个距离远，尽量停下来存魔法值，魔法值一超过10就用法术，当已走距离不小于原距离时，直接输出 i 并 break，如果时间到了还没走到，则输出目前走了的路程

Code:

#include
#define in scanf
#define out printf
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
using namespace std;  
int m,s,t,s1,s2;
int main() {
     
	fre(escape);
	in("%d%d%d",&m,&s,&t);
	for(int i=1;i<=t;i++) {
     
		s1+=17;//跑
		if(m>=10) {
     
			m-=10;
			s2+=60;//用法术  
		}
		else m+=4;  
		if(s2>s1) s1=s2;
		if(s1>=s) {
     
			out("Yes\n%d",i);
			return 0;
		}
	}
	out("No\n%d",s1);
	return 0;
}

T4

题目描述：

​ 给定A,B,C三根足够长的细柱，在A柱上放有2n个中间有空的圆盘，共有n个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的(下图为n=3的情形）。现要将 这些国盘移到C柱上，在移动过程中可放在B柱上暂存。要求:

(1)每次只能移动一个圆盘；

(2) A、B、C三根细柱上的圆盘都要保持上小下大的顺序；

任务:设An为2n个圆盘完成上述任务所需的最少移动次数，对于输入的n，输出An

比赛思路：

​ 这题就是个高精度的模板题，只要推出公式就可做

正解：

​ 首先我们要了解汉诺塔问题：有3个柱子A,B,C,一开始A柱上有N个盘子，按照从小到大的顺序插在A柱上，要求把这N个盘子从A柱上移动到C柱上，移动过程中必须保证不能把大盘子放置在小盘子之上，请你根据盘子数，计算出最少的移动次数。

​ 我们发现：

​ 当N=1时，次数=1

​ 当N=2时，可以先用N=1的方法将A柱上的1个盘子移到B柱，再将最下面的1个移到C柱，最后把B柱上的1个盘子移到C柱，整个过程用了两次N=1的操作和移动最下面的盘子的1次操作，因此最少移动次数=1×2+1=3

​ 当N=3时，可以先用N=2的方法将A柱上的2个盘子移到B柱，再将最下面的1个移到C柱，最后把B柱上的2个盘子移到C柱，整个过程用了两次N=2的操作和移动最下面的盘子的1次操作，因此最少移动次数=3×2+1=7

​ 当N=4时，可以先用N=3的方法将A柱上的3个盘子移到B柱，再将最下面的1个移到C柱，最后把B柱上的3个盘子移到C柱，整个过程用了两次N=3的操作和移动最下面的盘子的1次操作，因此最少移动次数=7×2+1=15

​ …

​ 当N=k时，可以先用N=k-1的方法将A柱上的k-1个盘子移到B柱，再将最下面的1个移到C柱，最后把B柱上的k-1个盘子移到C柱，整个过程用了两次N=k-1的操作和移动最下面的盘子的1次操作，因此最少移动次数=(k-1)×2+1

归纳，得当N=k时，
$$最少移动次数=2^k-1$$
理解了汉诺塔问题，这道题便迎刃而解了，由于有2N个盘子且按同样方式排列，所以
$$最少移动次数=2\times (2^k-1)=2^{k+1}-2$$
直接用高精度求出答案即可

Code：

#include
#define in scanf
#define out printf
#define rint register int
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
using namespace std;
const int D=1<<15;
int t,len,answer[100001]={
     0,1};
void ps(int f) {
     
	int jw=0,k=1;
	while(jw!=0 or k==1 or k<len) {
     //高精度
		answer[k]=answer[k]*f+jw; 
		jw=answer[k]/10;
		answer[k]%=10;
		k++;
	}
	len=max(len,k);
	return;
}
int main() {
     
	fre(hanoi);
	in("%d",&t);
	for(rint i=1;i<=(t+1)/15;i++) ps(D);//优化时间复杂度
	for(rint i=1;i<=(t+1)%15;i++) ps(2);
	for(rint i=len-1;i>=2;i--)
		out("%d",answer[i]);
	out("%d",answer[1]-2);
	return 0;
} 

End