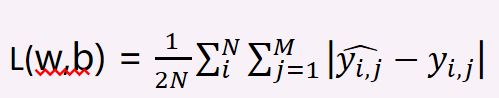【PyTorch】深度学习基础：神经网络

深度学习基础——神经网络

本博文是阅读机械工业出版社《PyTorch机器学习-从入门到实战》一书的随书笔记。

通过此部分，可以对整个神经网络的流程有一个较为全面的认识，内容涉及激活函数、前向算法、损失函数、后向算法以及PyTorch在其中支持的一些数据处理。

发展：神经元与神经网络

1. MP神经元模型：人工神经网络中的基本单元。

1943年由心理学家McCulloch和数学家Pitts参考生物神经元的结构提出

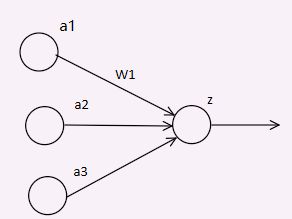
MP神经元从外部或者其他神经元接受输入信息，通过特定的计算得到输出结果。

如上图，x1和x2是输入信息；w1和w2是权重信息，b是偏置项。
通过计算z= w₁x₁+w₂x₂+b这样的方法整合带有权重的输入信息。
通过f：y = f(z)产生输出。

• MP模型中，权重的值是预先设置的，不能进行学习。
• 心理学家Hebb提出Hebb学习率，神经元开始学习之路。

2. 感知机(Perceptron)模型：不含隐层的前馈神经网络

1958年由心理学家Rosenblatt提出。

仅由两层（输入层和输出层）的神经元组成的神经网络叫感知机。

如图，每一个输入x_i都变成了单独的神经元，成为了输入单元。

• 感知机中的权重是通过训练得到的
• 类似逻辑回归模型，可以完成线性分类任务，但是学习能力十分有限。

p.s. 前馈神经网络

• 前馈神经网络时最早期也最简单的人工神经网络。
• 其包含多个神经元，被安排在不同的层，即输入层、隐含层、输出层，隐含层的个数可以有0个或多个。
• 在前馈神经网络中信息的传递只有一个——向前。

3. MLP(多层感知机)：含有1个或多个隐含层的前馈神经网络

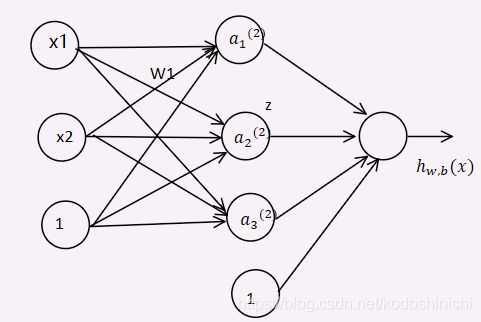
MLP可以很好地解决非线性可分的问题，我们常把类似于MLP这样的多层结构称为神经网络。

神经网络的学习或者训练，主要目的是通过学习算法得到神经网络解决指定问题所需的参数，包括连接权重和偏置项。

---

激活函数

激活函数(非线性函数)：
对于给定的输入，执行固定的数学运算得到输出结果，根据输出结果控制输入信息的保留程度。

1. 激活函数具有的性质

①非线性：一些复杂的问题往往是线性不可分的，需要引入一些非线性因素；而如果激活函数是线性的话，那么线性的叠加依然是线性的。
②连续可微性：梯度下降是神经网络学习和训练常用到的计算方法。
③值域有限：此时梯度下降的训练过程才会越来越稳定；特征表示受有限值的影响更加有效。
④单调性：只有激活函数是单调的时候，单层的神经网络才能保证为凸函数。
⑤具有单调导数的光滑函数
⑥函数值和输入近似相等：若满足这个条件，权重初始化成较小的随机数时神经网络的训练很高效；假设不满足这个条件，就需要很小心地初始化神经网络权重。

2. sigmoid函数

sigmoid函数，因为形状像s，又被称作s函数，其将输入变量映射到(0,1)之间；
对于特别大的输入，输出结果近似为1；对于特别小的输入，输出结果近似为0.

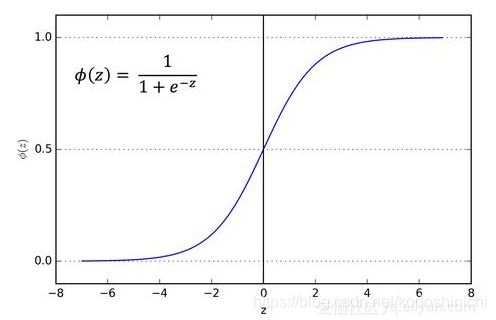
目前只会在特定的情境下使用，因为其具有自身的缺点：

• 梯度消失：当输入值趋于饱和（输入特别大或者特别小）时，函数曲线会趋于平缓，函数的梯度也会变得越来越小，直至趋于0，会导致经过神经元后得到的信息量很少，因此在初始化权重时要特别注意。
• 输出值不是零均值的：这样在后面的神经元上将会得到非零均值的输入。加入进入神经元的初始值是正的，那么反向传播中权重上的梯度也永远都会是正的。这会导致在权重梯度的更新上呈现锯齿形状。这一点可以通过不同bacth的权重和叠加得到不同的符号进行缓解。

本质原因是因为，按照下图如果想达到最优解，则两个参数w₀和w₁需要进行不同方向的变化（一增一减），但是因为sigmoid函数的作用，x₀和x₁两处变量的值总是保持同号，根据反向计算的链式法则，又知道参数变化的方向是正比于当前输入值的，所以只能够以一种迂回的z字形方式进行下降。

具体参考：《谈谈激活函数以零为中心的问题》

• 函数求导时涉及除法，在进行梯度下降时计算量较大。

3. Tanh函数

tanh函数与sigmoid函数不同的一点在于，它把输入变量映射到(-1,1)之间，也可以经由sigmoid函数得到——tanh(x) = 2δ(2x) - 1。

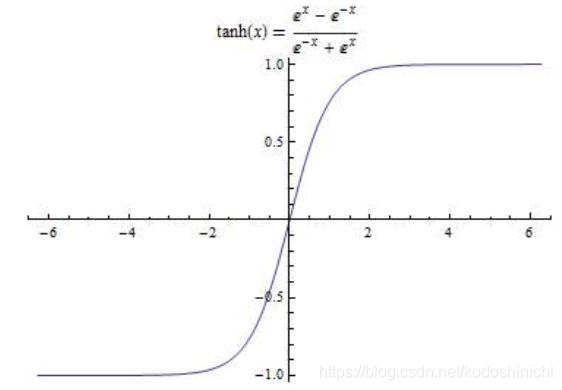
• tanh函数依然没有解决梯度消失的问题
• tanh函数是零均值的

因为梯度消失，不推荐在隐含层使用sigmoid或者是tanh函数；如果在输出层需要用到其二者，因为零均值问题，也首要推荐tanh函数。

4. Hard Tanh函数

Hard Tanh函数也是把输入变量映射到(-1,1)之间，但并不是通过公式计算，而是通过给定阈值直接得到最终结果。
标准的Hard Tanh函数把所有大于1的输入变成1，把所有小于-1的变成-1，其他的输入原样输出。

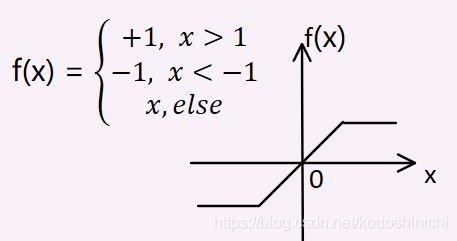
PyTorch中Hard Tanh支持指定阈值min_val和max_val以改变输出的最小值和最大值。
比如：对于f = Hardtanh(-2,2)的输出，所有大于2的输入变成2，所有小于-2的输入变成-2，其他保持原样。
m = nn.Hardtanh(-2,2)

5. ReLu函数

ReLu(Rectified Linear Unit)，线性整流函数，又称为修正线性单元，是一个分段函数：对于大于0的输入，保持原样输出；对于小于0的输入输出为0；在零点处虽然ReLu不连续，但是也同样适合做激活函数。

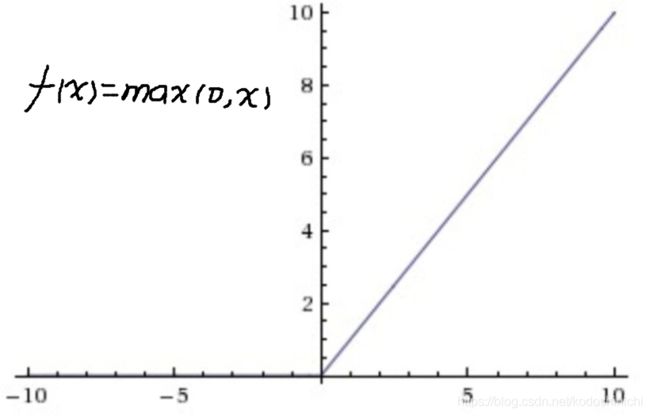
• 相比sigmoid或者tanh函数，ReLu只需要一个阈值就可以进行计算
• 因为ReLu是非饱和的，所以其在随机梯度下降的训练中会收敛得更快。

ReLu函数是目前应用最为广泛的激活函数，但它同样也具有脆弱性——经过一段时间的训练，一些神经元不再具有有效性，只会输出0（我们称ReLu单元发生了不可逆的死亡），特别是使用较大的学习率时。

• 解决：设置一个合适的学习率可以减少死亡现象的发生
• 应用：ReLu可以对生物学的研究成果进行很好的应用，也正是因为ReLu的死亡线性和生物神经“不是对所有外界信息都做出反应”这一特质相匹配。

6. ReLu拓展函数

为了解决以上所说的ReLu函数存在的问题，提出了ReLu的优化方案：当输入是小于0时，不再一味地输出0，通过一个很小的斜率为α的直线方程计算结果，α的不同取值对应着以下不同方案。

（1）Leaky ReLU
参数α（输入值小于0时α的斜率），决定泄露（leaky）的程度，一般取值为0.01；由此保证了，在输入值小于0的时候也有信息通过神经元，神经元不至于"死亡"。

（2）Parametric ReLU
对输入的每一个元素都运用函数PReLu(x) = max(0,x) + α *min(0,x) ,α是自学习的参数。

• nn.PReLU()这样调用时，在所有输入通道中均使用参数α
• nn.PReLU(nchannels)这样调用时，在指定通道的每个输入中使用参数α

（3）Randomized ReLU
RReLU是在比赛中提出的，其思想在于参数α是从高斯分布U(l,u)中随机生成的，后续可以在测试过程中进行修正。

有论文对于ReLU、Leaky ReLu和RReLU的效果进行了比较，还是ReLU的效果更优。

（4）Exponential Linear Unit（ELU）
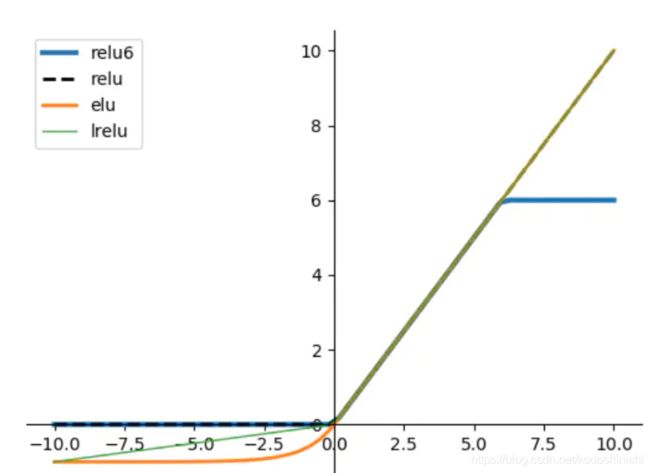
该激活函数比所有ReLU函数及其变体效果都要好

其结合了sigmoid和ReLU的优点，左侧软饱和，右边无饱和。

• 右侧可以缓解梯度消失的现象
• 左侧可以增强模型的鲁棒性
• 输出数据的均值接近于0，梯度下降的收敛速度会更快

图源：几种不同的激活函数

（5）Maxout

2013年由Ian J. Goodfellow提出。

前面所说的所有激活函数都是作用于输入信息的一个元素，输入信息间是没有关系的。
maxout单元并不是简单地作用于每一个输入元素z的函数g(z)，而是将z划分成具有k个值的组，然后输出其中一组最大的元素。

maxout具有很强的拟合能力，在足够隐含层的情况下可以拟合任意的凸函数。

7. Softmax与LogSoftmax

Softmax函数又被称作归一化指数函数，其可以把一个含任意实数的K维向量z“压缩”到另一个K维实向量σ(z)中，返回的是每个互斥输出类别上的概率分布，使得每一个元素的范围都在(0,1)之间，并且所有元素的和都为1.

它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。

一言以蔽之，求解的就是向量各个分量的幂指运算在幂指总和中的权重，权重越高，概率越大。
详情参考下方博文
《一分钟理解softmax函数》

softmax的函数形式通常如下：

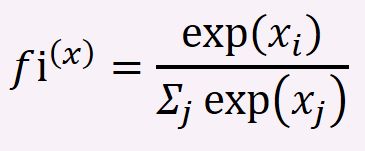
PyTorch中关于softmax的定义：

class torch.nn.Softmax(dim = None)

接收一个dim参数，用于指定计算softmax函数的维度，在该维度上输出的和应该为1.
对于一个二维的输入变量

• dim = 0时，按照列方向计算
• dim =1时，按照行方向计算
• 不指定时，会给出警告并按照dim = 1进行计算并输出结果。

import torch
from torch import nn as nn
from torch import autograd as autograd
m = nn.Softmax(dim = 1)
input = autograd.Variable(torch.randn(2,3))
print(input)
print(m(input))

'''
输出结果：
tensor([[-1.0440, -0.6643,  0.2725],
        [ 0.7247,  0.6124,  0.3263]])
tensor([[0.1615, 0.2361, 0.6024],
        [0.3898, 0.3484, 0.2617]])
'''

在应用softmax函数之前需要对输入值应用LogSoftmax函数

p.s. 该函数在PyTorch中的定义与用法与softmax相差无几

---

前向算法

1. 前向传播

我们使用前馈神经网络接收输入x并产生输出y ^hat时，信息通过网络向前流动。输入x提供初始信息，向输出的方向传播到每一层中的神经元，并跟相应的权重做运算，最终产生输出，这个过程就称为前向传播。

2. 图解

上图是一个含有四层的神经网络：第一层为输入层，第四层为输出层，中间的二三层为隐含层。

x₁和x₂是输入层中的两个神经元，h_i.^k是第i个隐含层的第k个神经元。

w_i,j^l表示第l层中第i个神经元到第l+1层中第j个神经元的权值。

图中的箭头即表示了信息传播流动方向，输入层-隐含层-输出层。

3. 信息计算

前向传播过程中，每一个神经元的值就是所有输入到该神经元的信息和相应连接上的权重的加权求和之后，再进行非线性作用后的结果。

拿第一隐含层的两个神经元举例说明：

Z_h11 = x₁ * w_1,1¹ + x₂ * w_2,1¹ + b₁
y_h11 = f(Z_h11)

Z_h21 = x₁ * w_1,2¹ + x₂ * w_2,2¹ + b₂
y_h21 = f(Z_h21)

其中Z表示线性加权和，y表示神经元最终的输出值，b是偏置项。

隐含层中每一个神经元的输出值，随着信息的传递和流动，同时也是下一层网络的输入信息。按照这个过程，我们可以逐步计算得到输出层神经元的值，就完成了一次完整的前向传播。

4. 意义
前向传播是使用神经网络进行输出预测的过程（每一个训练集的实例，通过层层计算最终得到整个网络的输出），得到的输出值与真实值（训练集中每个实例的标签）的差别可以用来评估当前参数权重的好坏。

往下几个部分我们会讲到另一方向的信息流动——反向传播，此处可以两者结合在一起理解一下神经网络的作用过程。

从神经网络的最后一个隐含层开始，计算每一层对整体的差别“贡献”了多少，这个过程就是反向传播。

---

损失函数

1. 概念

（1）定义
损失函数(Loss function)，又称为代价函数，常表示为L。损失函数用来量化在训练过程中网络输出和真实目标间的差距，损失函数是神经网络中特殊的层。

最常用的一个损失函数就是平方误差损失，即把数据集中每一个实例得到的预测值和真实值之间的差异求平均，用这个平均误差可以整体反映神经网络的好坏情况。

（2）作用
损失函数的出现使得网络的训练过程变成一个优化问题；确定神经网络的最佳状态相当于找到使损失最小的神经网络参数。

（3）目标函数= 经验风险 + 结构风险
损失函数L的均值称为经验风险函数，但并不是经验风险越小就越好，比如模型过拟合时，虽然经验风险小，但是模型是不可取的。

解决过拟合问题常常引入正则化。正则化又叫结构风险，表示模型的复杂程度。
经验风险和结构风险的和称为目标函数，神经网络训练的最终目的就是寻找最佳的参数，使得目标函数最小。

以下讲解损失函数的类型，大体上根据问题的类型分为两种，回归问题的损失函数和分类问题的损失函数。

2. 回归问题

（1）MSE（mean squared error）：均方差损失
回归问题的输出是实数值（一个实数值或者一个实数向量），采样的平方损失函数有点类似于线性回归的最小二乘法

①单输出的MSE表达式

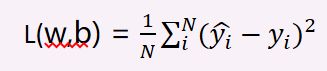
其中，N表示数据集中训练实例的个数，y^hat表示预测值，y表示真实值。

②多输出的MSE表达式

其中，N表示数据集中训练实例的个数，M表示输出的个数，y^hat表示预测值，y表示真实值。

对于MSE，通常会乘上系数1/2，因为对于参数优化问题来说，系数的扩大或缩小不会影响极值点的求解，但是1/2的系数对于MSE的求导运算可以减少计算量。

③特点：
MSE使用广泛，但是对异常值很敏感（均值，平方这些因素的共同作用）。在某些特定的任务中需要考虑异常值的作用，就需要一个关注中位数而非平均值的中位数。

（2）MAE（mean absolute error）：平均绝对误差

MAE是数据集上所有误差绝对值的平均数。

意义上同，不再解释。

3. 分类问题
神经网络可以解决两类分类问题：
其一，判定输入实例属于哪一个类别；其二，给出输入实例属于某一个类别的概率。

（1）Hinge Loss——类别分类
对于0-1分类问题，可采用hinge loss，其中用两个数值（通常是-1和1）表示这个实例是否属于这个类别。

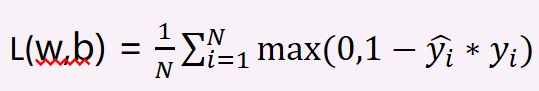
Hinge loss只能用于解决二分类的问题，可以采用一对多的策略将多分类问题转换为二分类问题，每次只考虑是否属于某一个特定的类别，可以把一个N分类问题转换成N各二分类问题。

（2）负对数似然损失函数——概率分类

负对数似然函数本质上和交叉熵函数是一致的。

交叉熵是不确定信息的一种度量，用交叉熵来理解这里的损失函数，相当于是度量我们学习到的y^hat和真实值y之间的不确定性。

p.s. 之前在一篇讲解逻辑回归的文章中也有提到“对数似然函数和交叉熵函数”的等价性问题，有兴趣的读者可以参考《机器学习算法系列（3）：逻辑斯蒂回归》

4. PyTorch中常用的损失函数

PyTorch中对于常用的损失函数都做了封装，可以在系统中直接进行调用。

（1）MSELoss
定义：

class torch.nn.MSELoss(size_average = True, reduce = True)

参数解释：

• reduce默认情况下为true。为true时会根据size_average的取值选择是返回每个minibatch的和还是平均值；为false时，不再考虑size_average的取值，直接返回每个元素的损失。
• 在 reduce为true的时候才予以考虑，缺省值为true。为true时损失取的是每个minibatch的损失平均；为false时，返回的损失每个minibatch的损失之和。

使用示例：

import torch
from torch import nn as nn
from torch import autograd as autograd

loss = nn.MSELoss()
input = autograd.Variable(torch.randn(3,5),requires_grad = True)#随机输入值
target = autograd.Variable(torch.randn(3,5))#随机目标值
output = loss(input,target)#按照MSE 计算输入与目标之间的差异
output.backward()#调用backward进行梯度计算
print("input:",input)
print("target",target)
print("output",output)

'''
input: tensor([[ 0.7129, -0.2203,  0.6206,  0.7164, -0.0434],
        [-0.0893,  0.4532, -0.2532,  1.8048, -0.8380],
        [-0.1634,  1.3425,  0.7831, -0.1677, -2.0653]], requires_grad=True)
target tensor([[-0.5880, -0.8215, -0.4290, -1.5599, -0.0277],
        [-0.0279,  0.5446, -1.0769,  0.7079, -0.0297],
        [ 0.3958, -0.7714,  0.5840,  0.1859, -0.0419]])
output tensor(1.3283, grad_fn=)
'''

（2）L1Loss(MAELoss)
定义：

class torch.nn.L1Loss(size_average = True,reduce = True)

参数解释和使用方法与MSE相同，不再赘述。

（3）BCELoss

BCELoss 用在二分类问题中

BCELoss对应的数学计算就是对数似然损失函数对于N个样本取平均的结果。

定义：

class torch.nn.BCELoss(weight = None,size_average = True)

参数解释：

• weight指定batch中每个元素的Loss权重，必须是一个长度和batch相等的Tensor。
• size_average与前面相同，缺省值为true。为true时表示每个mini_batch上的损失均值；为false时表示每个mini_batch上的损失之和。

使用示例：

BCELoss在使用时要求每个目标值都要在(0,1)之间，这一点可以借助sigmoid函数来实现。

p.s. 在最后进行损失计算前，最后一层使用sigmoid函数进行非线性激活。

import torch
from torch import nn as nn
from torch import autograd as autograd

m = nn.Sigmoid()
loss = nn.BCELoss()
input = autograd.Variable(torch.randn(3),requires_grad = True)
target = autograd.Variable(torch.FloatTensor(3).random_(2))
output = loss(m(input),target)
output.backward()
print("input:",input)
print("m(input):",m(input))
print("target",target)
print("output",output)

'''
input: tensor([1.1908, 0.1135, 2.3812], requires_grad=True)
m(input): tensor([0.7669, 0.5284, 0.9154], grad_fn=)
target tensor([1., 1., 0.])
output tensor(1.1243, grad_fn=)
'''

（4）BCEWithLogitsLoss
定义：

class torch.nn.BCEWithLogitsLoss(weight = None,size_average = True)

参数解释和使用示例与BCELoss基本相同，不再赘述。

下面这篇博文《PyTorch详解BCELoss和BCEWithLogitsLoss》比较直观地讲述了两个函数是怎样对损失值进行计算的，读者可以参考。

BCEWithLogitsLoss也是在二分类方法中使用，它的作用机制是把sigmoid函数与BCELoss集成在一起，在实际应用中，BCRWithLogitsLoss的作用机制比sigmoid函数加上BCELoss的机制要更加稳定，因为把两个层合并时可以使用LogSumExp的优势来保证数值的稳定性。

【关于LogSumExp】
参考文章《知乎上讨论关于LogSumExp》
笔者根据自己的思路把ogSumExp的问题思路进行了整理，如下图：



在文末原作者利用线性近似的方法，对LSE函数进行了分析和讨论，并作出了以下结论：可以说LSE计算实质上是针对max函数的一种平滑操作，从计算效果上来说，LSE才是真正意义上的softmax函数。

（5）NLLLoss

NLLLoss使用在多分类任务场景中的负对数似然损失函数，如果用C表示多分类任务中类别的个数，N表示minibatch，则NLLLoss必须是(N,C)的二维Tensor——数据集中的每个实例对应每个类别的对数概率。

前面也讲过了，这需要对输入值配合softmax函数来使用，可以在网络的最后一层应用LogSoftmax层来实现。

定义：

class torch.nn.NLLLoss(weight = None,size_average = True,ignore_index = -100,reduce = True)

参数解释：

• size_average和reduce两个属性均和前面的设定相同，不再赘述
• weight用来为每个类别计算损失时赋权值，如果类别的个数为C，那么应该传入一个一维的长度为C的Tensor,当训练集不平衡的时候这个参数很有用。
• ignore_index用于设置一个可忽略值，使这个值不会影响到梯度的计算。同样，如果 size_average设置为true时，计算loss的平均值时该项也会被忽略。

（6）CrossEntropyLoss
定义：

class torch.nn.CrossEntropyLoss(weight = None,size_average = True,ignore_index = -100,reduce = True)

参数解释和NLLLoss大致相同，不再赘述。

CrossEntropyLoss函数也是多分类应用场景使用的交叉熵损失函数，它之于NLLLoss的关系就好比BCEWithLogitsLoss之于BCELoss的关系。

前两者针对的是多分类问题，后两者针对的是二分类问题（二分类同样也可以解决多标签分类问题，采用一对多或一对一策略）。

CrossEntropyLoss函数把LogSoftmax函数和NLLLoss函数结合在一起，因此可以使用NLLLoss的任务也都可以用CrossEntropyLoss进行解决，且后者更加简洁。

同样地，下面这篇博文对于两种损失函数的计算实质给出了详细的说明和比较：
关于交叉熵的操作，总结得很地道的一句话就是“与label项对应的那个值拿出来，取负值，再求均值”所求的就是模型训练出来的交叉熵”。
《PyTorch详解NLLLoss和CrossEntropyLoss》

---

反向传播算法

反向传播（BP）——Backpropagation是1986年由Rumelhart和McCelland为首的科研小提出，并发表在Nature中的论文《Learning representations by back-propagating errors》.

反向传播算法基于梯度下降，是链式求导法则的应用，它以误差为主导进行的反向传播计算运动。

1. 基本思想：
希望可以通过输出值和期望的输出值之间的差异来间接调整权值——

根据输出层的误差，计算在最后一个隐含层中的每个神经元对输出层误差有多少影响，其前一层隐含层的影响度又由这一层隐含层的误差信息计算出来。

按照上述思路，直到计算到输入层。

本文不对BP的数学进行过多推算，只讲述在PyTorch中的相关应用。

2. PyTorch对BP的封装与支持
PyTorch中所有神经网络的核心是autograd自动求导包，该包的核心是Variable类，该类封装了tensor并支持tensor的所有操作。
以下给出PyTorch中常用的包之间的相互关系，以及针对tensor常用的计算。

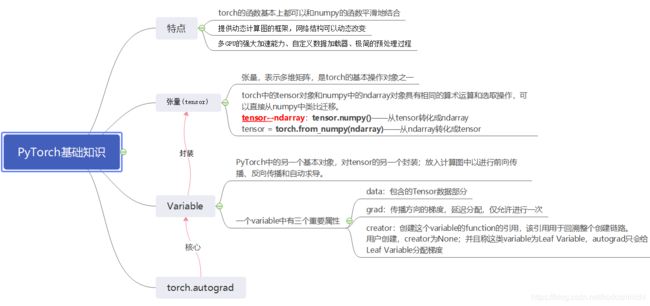
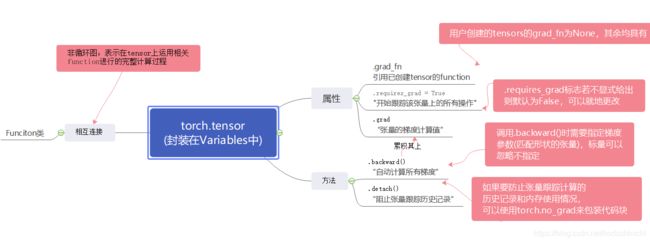
在程序中一旦完成了有关于tensor的所有前向运算之后，就可以直接调用backward()方法，所有的梯度就会自动计算。
p.s. 上一陈述成立是基于在声明tensor张量的时候，对于requires_grad属性设置为true，允许跟踪相关计算过程和内存使用情况。

3. 程序示例

import torch 
from torch import autograd
from torch.autograd import Variable

x = Variable(torch.ones(2,2),requires_grad = True)#创建变量
print("x:",x)
#对variable的操作
y = x+2
print("y:",y)
#继续对y进行操作
z = y*y*3
out = z.mean()
print("z:",z)
print("out:",out)
print("grad:",x.grad)

#以上关于out的前向计算结束了，可以调用backward()函数
out.backward()
print("grad:",x.grad)

'''
x: tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
y: tensor([[3., 3.],
        [3., 3.]], grad_fn=)
z: tensor([[27., 27.],
        [27., 27.]], grad_fn=)
out: tensor(27., grad_fn=)
grad: None
grad: tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])
        '''