MATLAB 四点定球及三点定圆(完整代码)

哈哈哈看到一个很有意思的想法，顺手写了一下：
怎样快速求圆形或球形的隐函数方程、中心、半径
先从四点定球开始：

四点定球

实际上是看到李扬老师的视频哈哈哈

求通过不共面四点$M_1\left(x_1,y_1,z_1\right)$,$M_2\left(x_2,y_2,z_2\right)$, $M_3\left(x_3,y_3,z_3\right)$, $M_4\left(x_4,y_4,z_4\right)$的球面方程

我们设球面方程为：
$$a\left(x^2+y^2+z^2\right)+bx+cy+dz+e=0$$

那么球面上的任意点及已知四点满足如下方程组：

$$\{\begin{array}{l}a\left(x^2+y^2+z^2\right)+bx+cy+dz+e=0\\ a\left(x_1^2+y_1^2+z_1^2\right)+b{x}_1+c{y}_1+d{z}_1+e=0\\ a\left(x_2^2+y_2^2+z_2^2\right)+b{x}_2+c{y}_2+d{z}_2+e=0\\ a\left(x_3^2+y_3^2+z_3^2\right)+b{x}_3+c{y}_3+d{z}_3+e=0\\ a\left(x_4^2+y_4^2+z_4^2\right)+b{x}_4+c{y}_4+d{z}_4+e=0\end{array}$$

要使方程组有非零解则要求系数行列式为0，即：
$$D(x,y,z)=\left|\begin{array}{lllll}{x}^2+y^2+z^2& x& y& z& 1\\ x_1^2+y_1^2+z_1^2& x_1& y_1& z_1& 1\\ x_2^2+y_2^2+z_2^2& x_2& y_2& z_2& 1\\ x_3^2+y_3^2+z_3^2& x_3& y_3& z_3& 1\\ x_4^2+y_4^2+z_4^2& x_4& y_4& z_4& 1\end{array}\right|=0$$

这时候我们发现约束条件$D(x,y,z)=0$是关于x,y,z的隐函数，且由x,y,z的任意性，得出$D(x,y,z)=0$正是我们所要求的球面方程。

当然我们要是想单独求某个系数也非常简单，例如求b只需要求如下行列式:
$$\left|\begin{array}{lllll}0& 1& 0& 0& 0\\ x_1^2+y_1^2+z_1^2& x_1& y_1& z_1& 1\\ x_2^2+y_2^2+z_2^2& x_2& y_2& z_2& 1\\ x_3^2+y_3^2+z_3^2& x_3& y_3& z_3& 1\\ x_4^2+y_4^2+z_4^2& x_4& y_4& z_4& 1\end{array}\right|$$

结论成立实践开始，我们编写如下方程：

function [Func,Mu,R]=getBall(X,Y,Z)
syms x y z
symMat=[x.^2+y.^2+z.^2,x,y,z,1];
varMat=[X(1).^2+Y(1).^2+Z(1).^2,X(1),Y(1),Z(1),1;
        X(2).^2+Y(2).^2+Z(2).^2,X(2),Y(2),Z(2),1;
        X(3).^2+Y(3).^2+Z(3).^2,X(3),Y(3),Z(3),1;
        X(4).^2+Y(4).^2+Z(4).^2,X(4),Y(4),Z(4),1];

% 计算球隐函数
Func=matlabFunction(det([symMat;varMat])==0);

% 计算各个参数
a=det([1 0 0 0 0;varMat]);
b=det([0 1 0 0 0;varMat]);
c=det([0 0 1 0 0;varMat]);
d=det([0 0 0 1 0;varMat]);
e=det([0 0 0 0 1;varMat]);

% 计算球心，半径等信息
Mu=-[b,c,d]./a./2;
R=sqrt(sum(Mu.^2)-e./a);
end

其中返回值Func为球面隐函数，Mu为球心，R为半径

使用实例：

pnt=[0,0,1;1,1,6;1,3,4;9,6,11];
scatter3(pnt(:,1),pnt(:,2),pnt(:,3),'filled')
hold on

[~,Mu,R]=getBall(pnt(:,1),pnt(:,2),pnt(:,3));
[X,Y,Z]=sphere(40);
mesh(X.*R+Mu(1),Y.*R+Mu(2),Z.*R+Mu(3),'FaceColor','none')

三点定圆

原理一模一样只不过少了个z而已：

function [Func,Mu,R]=getCircle(X,Y)
syms x y z
symMat=[x.^2+y.^2,x,y,1];
varMat=[X(1).^2+Y(1).^2,X(1),Y(1),1;
        X(2).^2+Y(2).^2,X(2),Y(2),1;
        X(3).^2+Y(3).^2,X(3),Y(3),1];

% 计算圆隐函数
Func=matlabFunction(det([symMat;varMat])==0);

% 计算各个参数
a=det([1 0 0 0;varMat]);
b=det([0 1 0 0;varMat]);
c=det([0 0 1 0;varMat]);
d=det([0 0 0 1;varMat]);

% 计算圆心，半径等信息
Mu=-[b,c]./a./2;
R=sqrt(sum(Mu.^2)-d./a);
end

使用实例：

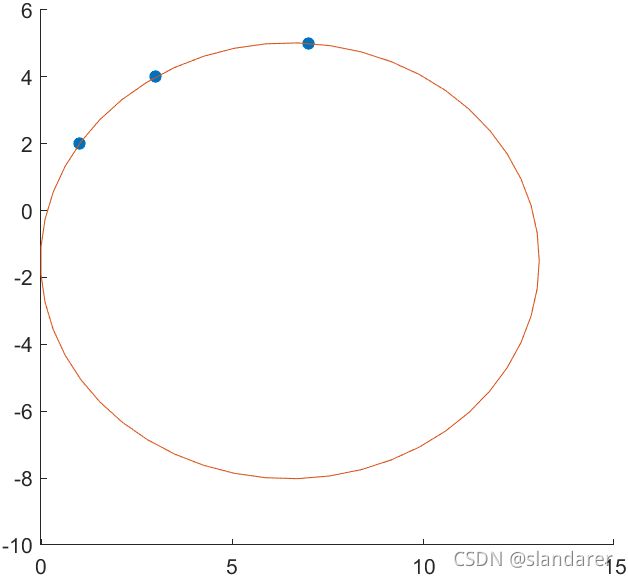
pnt=[1 2;3 4;7 5];
scatter(pnt(:,1),pnt(:,2),'filled')
hold on

[~,Mu,R]=getCircle(pnt(:,1),pnt(:,2));
t=linspace(0,2*pi,50);
plot(cos(t).*R+Mu(1),sin(t).*R+Mu(2))

---

当然这种方法也同样适合很多其他情况，例如两点共线，或者求一些其他曲面的参数之类的，可以自行探索一下。