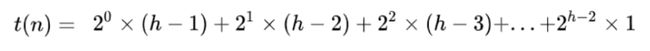✨✨[数据结构]——最经典的七大排序（超详细近两万字教程，你值得拥有）✨✨

---

常见的排序算法：

插入排序：直接插入排序，希尔排序

选择排序：直接选择排序，堆排序

交换排序：冒泡排序，快速排序

归并排序：归并排序

一，插入排序

定义：插入排序的算法思想非常简单，就是每次将每次待排序序列中的 一个记录，按照其关键字值的大小插入
已经排好的记录序列中的适当位置上。关键就在于如何确定待插入的位置。 此文章只介绍其中的两种排序方式（直接插入排序，希尔排序）.

1，直接插入排序

（1）基本思想

首先存在一组待排序的记录，首先将这一组中的第一个记录构成有序子序列，而剩下的记录序列构成无序子序列，然后每次将无序序列中的第一个记录，按照其关键字值的大小插入前面已经排好序的有序序列中，并使其仍然保持有序。（这种排序是通过顺序查找来确定待插入的位置的）

（2）主要步骤

a，首先将待排序的记录存放在数组a[0…n]中。

b，创建变量end，用来表示前面有序序列中的记录个数，将a[end+1] 暂存在临时变量tmp中（这就是无序序列中的第一个记录，准备插入前面的有序序列）。

c，将tmp与a[end] 进行比较，如果tmp的值小于a[end]，那么就将a[end]后移一个位置，然后end自减，让tmp继续与a[end]进行比较，直到tmp的值大于a[end]。

d，将tmp的插入第a[end+1]的位置。

e，令end=0，1，2，3，…，n-1，重复步骤b，c，d。

（3）代码实现

//假设要求是升序排序
//基本思想：[0,end],是有序的，end+1位置的值插进去，使得[0，end+1]也有序。
void InsertSort(int *a,int n)
{
     
	for (int i = 0; i < n - 1; i++)//如果i能等于n-1的话，将i赋给end，end+1就会直接越界了。（所以最大就是n-2）
	{
     
		int end = i;
		int tmp = a[end + 1];//先将a[end+1]的数值保存起来，防止a[end + 1]被覆盖。
		while (end >= 0)//这个循环只负责将指定的end+1的值插进数组，想排序整个数组，还需要外面的for来遍历end。
		{
     
			if (a[end] > tmp)
			{
     
				a[end + 1] = a[end];
				end--;
			}
			else
			{
     
				break;
				//有两种break的情况。
		        //1，这个要插入的数tmp太小了，是数组中最小的，end一直自减，直到end<0,然后直接从while循环中跳了出来。这时候                   end指向-1，然后将tmp直接赋到a[end+1]上。
		        //2，如果tmp比a[end]大了，那么直接break，然后进行赋值。
			}
		}
		a[end + 1] = tmp;//break之后，为两种情况进行赋值。
	}
}
int main()
{
     
	int a[] = {
     3,5,2,7,8,6,1,9,4,0};
	int n = sizeof(a) / sizeof(a[0]);
	InsertSort(a, n);
    for (int i = 0; i < n; i++)//最后可以测试一下，最终输出的结果是0，1，2，3，4，5，6，7，8，9
	{
     
		printf("%d ",a[i]);
	}
}

（4）性能分析

a，空间复杂度：排序过程中仅仅用了一个辅助单元a[0]，因此空间复杂度为O（1）。

b，时间复杂度：看最坏的情况，在逆序的时候，每一趟排序都要将待插入的记录插入到记录表的最前面的位置。总的比较次数是一个等差数列，1+2+3+…+n-2，总共n（n-1）/2，总的移动次数是大约也是n（n-1）/2，所以时间复杂度就是O（n^2）。

c，算法稳定性：直接插入排序是一种稳定的排序算法。

d, 优点：如果原来数组很接近有序，那么时间复杂度就非常接近O（n）。

2，希尔排序

(1) 基本思想

希尔排序也是一种插入排序，它是直接插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序。希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。大体分为：先进行预排列，让数组接近有序 然后再直接插入排序。

(2) 主要步骤

举个例子 ：（使之变成升序）

9，8，7，6，5，4，3，2，1，0

a,先分组，创建变量gap，然后间隔为3的为一组，可以设gap为3。

9，6，3，0一组，8，5，2一组，7，4，1一组。

b,分完组之后，将每一组都使用直接插入排序按顺序排好。最后就是：0，2，1，3，5，4，6，8，7，9。

c，以上为gap=3的时候进行的分组排序，可以逐次让gap减小，使得序列更加接近有序，最终令gap=1再进行一次排序，这个时候一定变成有序了，因为当gap=1的时候就相当于是直接插入排序了。

d，图片大概实现：

(3) 代码实现

void ShellSort(int* a,int n)//这个循环也就是翻版的直接插入排序，唯一的不同就是将1换成了gap。
{
     
	int gap =  n;
	while (gap > 1)
	{
     
		gap = gap / 2;
		for (int i = 0; i < n - gap; i++)//把间隔为gap的多组数据同时排。
		{
     
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)//这个while完成的任务仅仅是end+gap这一个的插入，还没有将这它所在的同为gap间隔的其他数据进行排序。
			{
     
				if (tmp < a[end])
				{
     
					a[end + gap] = a[end];
					end = end - gap;
				}
				else
				{
     
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}	
}
void ArraySrot(int* a,int n)//负责输出数组遍历结果
{
     
	for (int i = 1; i < n; i++)
	{
     
		printf("%d ",a[i]);
	}
}
int main()
{
     
	int a[] = {
      9,8,7,6,5,4,3,2,1,0};
	int n = sizeof(a) / sizeof(a[0]);
	ShellSort(a,n);
	ArraySrot(a,n);
	return 0;
}

(4) 性能分析

a，空间复杂度：希尔排序中用到了直接插入排序，而直接插入排序 的空间复杂度为O（1），所以，希尔排序的空间复杂度时O（1）.

b，时间复杂度：希尔排序的时间效率分析很困难，因为关键字的比较次数与记录的移动次数依赖于增量序列的选取。目前还没有一种选取最好的增量序列的方法。经过大量研究，选取一些增量序列可以使得其时间复杂度达到O（n^7/6次方），这就很接近O（n*logn）。

c，算法稳定性：不稳定，由于子序列的元素之间跨度较大，所以移动时就会引起跳跃性的移动。一般来说，如果排列过程中的移动是跳跃性的移动，则这种排列就是不稳定的排序。

二，选择排序

1，直接选择排序

（1）基本思想

每一次从待排序的数据元素中选出最小（最大）的一个元素，放在序列的起始位置，直到全部的待排序元素排完。

（2）主要步骤

这个排序过程并不复杂，可直接通过代码来理解。

（3）代码实现

因为此排序的效率较低，所以可以在原基本思想的基础上做一些优化：一次性选两个最值，分别放到序列的开始以及结尾位置。

//这个写个优化版本的，一次选两个数，一个最大的，一个最小的。这样效率可以快一倍
void SelectSort(int*a,int n)
{
     
	int begin = 0, end = n - 1;//创建两个整型变量，一个指向数组的起点，一个指向数组的终点
	while (begin < end)
	{
     
		int mini = begin, maxi = begin;//刚开始最小值的下标和最大值的下标都指向begin处的值
		for (int i = begin; i <= end; ++i)//从起点开始向重点开始遍历,进行完一遍这个for循环可以选出数组中的一个最大值和一个最小值的下标
		{
     
			if (a[i] < a[mini])
			{
     
				mini = i;
			}
			if (a[i] > a[maxi])
			{
     
				maxi = i;
			}
		}
		Swap(&a[begin], &a[mini]);//最小的值换到最左边
		
		if (begin == maxi)
		//如果不加这个判断条件就会出现bug，因为原先的经过for循环已经确定了最大（maxi）和最小值（mini）的下标，但如果begin（下标为0）和maxi（下标也是0）重合了即最大的数恰好是数组中第一个数a[0]，经过Swap，begin和mini的会进行数值交换，a[0]保存的变成了最小值，但是maxi标记的位置还是a[0]的位置，所以经过下面的Swap（& a[end], &a[maxi]）交换的话会把最小值换到a[end]处
		{
     
			maxi = mini;//更改一下maxi的值（maxi是最大值的下标），使他重新指向最大值
		}
		Swap(& a[end], &a[maxi]);//最大的值换到最右边
		begin++;
		end--;
		//经过依次这样的循环，整个数组待排序的数就变成了n-2个
	}
}

void Swap(int* child, int* parent)//交换数值函数
{
     
	int tmpt = *child;
	*child = *parent;
	*parent = tmpt;
}

（4）性能分析

a，空间复杂度：O（1），直接选择排序过程中，交换时要使用一个辅助单元。

b，时间复杂度：O（n^2），外循环控制循环的趟数，共需执行n-1次，内循环是控制每趟排序与关键字值比较的次数，需要执行n-2i（还剩下的次数），总的比较次数就是1/4 n*（n-1），时间复杂度就是O（n^2）。

c，算法稳定性：不稳定，虽然可以人为地控制相同的数字谁在前谁在后，但是在换位置的时候可能会影响其他的相同数字的相对位置。

2，堆排序

（1）基本思想&主要步骤

堆排序是一种选择排序，借助堆来实现这种排序。堆：逻辑结构是一棵完全二叉树，实际结构是一个数组。

（2）大堆和小堆

大堆要求：树中所有的父亲都是大于等于孩子的。

小堆要求：树中所有的父亲都是小于等于孩子的。

问题：为什么要用它来实现排序呢？

答：大堆可以保证堆顶的元素是最大的。小堆可以保证堆顶的元素是最小的。根据这个可以进行排序。如果有个数组想要排序，那么就先把它建成个堆（大堆或小堆）。逻辑上是：完全二叉树。

（3）父子结点

父子结点序号可以通过关于数组中的下标的公式来计算。

leftchild （左孩子）= parent*2+1

rightchild （右孩子）= parent*2+2

parent = (child-1)/2//无论是左孩子还是右孩子，他们的父亲结点都满足这个公式。

（3）主要步骤

首先将一个无序序列构造成一个初始堆（大堆或者小堆）（假设是大堆），再将堆顶最大值结点与最后一个结点（下标n-1）进行交换，交换后再调整构造成第2个堆，接着，再将堆顶大值结点与最后第2个结点（下标n-2）交换，交换后再调整构造成第3个堆，如此反复，直到整个无序子表只有一个元素为止，堆排序完成。

（4）向下调整法

在将无序序列（前提，其左右子树都必须是小堆。）构造成初始堆的时候需要用到这个方法（就是将左右子树都是小堆的无序序列调整成小堆，说白了使用这个方法导致的变化就是将根这一个数融入整个小堆。）

具体操作：按小堆为例子，选出左右孩子中小的那个，跟父亲比较，从根结点开始，如果比父亲小就交换。交换完之后，父亲作为小的二叉树的父亲继续向下比较交换。交换的只是数值。一直到叶子结点就终止。然后就变成了小堆。（如果左右子树有空的，空也算是小堆）

void Swap(int* child, int* parent)//交换
{
     
	int tmpt = *child;
	*child = *parent;
	*parent = tmpt;
}
void AdjustDown(int* a,int n ,int root)//向下调整算法（这里默认是小堆）
{
     
	int parent = root;
	int child = parent * 2 + 1;//默认child是左孩子
	while (child<n)//调到叶子就中止
	{
     
		//1,选出左右孩子中小的那一个。
		if (a[child + 1] < a[child]&& child+1<n )//这里的child+1可能会越界，所以再加一个条件。
		{
     
			child++;
		}
		if (a[child] < a[parent])
		{
     
			Swapt(&a[child], &a[parent]);//就直接交换,交换的是双方的数值。
			parent = child;//这个交换的是在二叉树中的位置。
			child = parent * 2 + 1;
		}
		else
		{
     
			break;
		}
	}
}

以上的操作时建立在左右子树都是小堆的前提下。但是如果上面操作的无序序列的左右子树并不是小堆的话，就不能直接按以上的操作来了，就需要先将这个无序序列调整成左右子树都是小堆的形式。那么这个调整肯定是从底向上调整的。从最后一个非叶子结点（最后一个叶子结点的下标是n-1,找到它的父亲，然后从它的父亲开始就是非叶子结点）从这里开始向下调整，然后一直向上蔓延，一直到头结点为止。

（5）特别注意

排升序要建大堆。不能建小堆。

因为：排升序肯定是将最小的一个一个的拿出来。如果是小堆，它最小的数值在堆顶，将它拿出来之后，如果还想再拿次小值，但是剩下的树结构都已经乱掉了，需要重新从头建堆，而建堆的时间复杂度是O（n），那么这样堆排序就没有优势了。

重新建堆选数的时间复杂度是O（n），要再选n-1个数，也就是要进行重新建堆选数的次数是n-1次，那么总的堆排序的算法就是O（n方）。

将0这个最小值拿出来之后，就不再管0了，然后对剩余的树结构再重新建堆。这样就没有优势了。

你这样每次都是O（n），还不如直接遍历呢，遍历的时间复杂度也是O（n），遍历一遍选出最小的数，拿出来，然后再遍历选。。。，何必还要有堆排序这种算法呢？

正确的做法：建大堆，然后将最大的数与最后的数进行交换。

（6）代码实现

void Swap(int* child, int* parent)//交换数值
{
     
	int tmpt = *child;
	*child = *parent;
	*parent = tmpt;
}
void AdjustDown(int* a,int n ,int root)//向下调整算法（这里默认是小堆）
{
     
	int parent = root;
	int child = parent * 2 + 1;//默认child是左孩子
	while (child<n)//调到叶子就中止
	{
     
		//1,选出左右孩子中小的那一个。
		if (a[child + 1] > a[child]&& child+1<n )//这里的child+1可能会越界，所以再加一个条件。
		{
     
			child++;
		}
		if (a[child] > a[parent])
		{
     
			Swap(&a[child], &a[parent]);//就直接交换,交换的是双方的数值。
			parent = child;//这个交换的是在二叉树中的位置。
			child = parent * 2 + 1;
		}
		else
		{
     
			break;
		}
	}
}
void HeapSort(int* a, int n)//堆排序
{
     
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)//从最后一个非叶子的子树开始调,一直向上调。这就完成建堆了。
	{
     
		AdjustDown(a, n, i);
	}
	int end = n - 1;//找到最后位置的下标。
	while (end > 0)//当只有一个值的时候停止。
	{
     
		Swap(&a[0], &a[end]);//交换当前堆中的最大和最小值。
		AdjustDown(a, end, 0);//这个时候已经算是将最大的那个数排除出去了，还剩n-1个，然后再进行向下调整构建新树。
		end--;//每次都会排除出去最大的一个。
	}

}

int main()
{
     
	int a[] = {
     3,5,2,7,8,6,1,9,4,0};
	int n = sizeof(a) / sizeof(a[0]);
	HeapSort(a,n);
	return 0;
}

（7）性能分析

a，空间复杂度：O（1），堆排序需要一个记录的辅助存储空间用于结点之间的交换。

b，时间复杂度：O（n*logn），计算公式就是:向下调整算法的时间复杂度 * 向下调整的次数。

建堆的时间复杂度是多少呢？

最终的复杂度不是所谓的O（n*logn）。而是O（n）

取最坏的情况：是一个满二叉树。

公式：每一层结点的个数*结点最多调整的次数的和。

这样的一个二叉树，设高度为h。

每一层的结点个数（从第一层开始）：2^h-4， 2^h-3，2^h-2，2^h-1。

最多调整的次数(从第一层开始):h-1，h-2，h-3，h-4。

然后将他们对应相乘再相加出来就是时间复杂度。

整理一下：

进行错位相减法。算出来之后就是n-logn，也就是O(n).

向下调整最多调整多少次呢？ 树的高度次。高度次就是logn次。我有n个数需要选择进行向下调整。

所以时间复杂度就是n*logn。

所以，最后的时间复杂度就是O（n*logn）。

c，算法稳定性：不稳定，在建好堆以后数会进行交换，会影响相对位置。

三，交换排序

1，冒泡排序

（1）基本思想

所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排序的特点就是将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

（2）主要步骤

结合代码

（3）代码实现

void BubbleSort(int* a, int n)
{
     
	for (int i = 0; i < n; i++)//将最大的数，次大的数一个一个的放在最后面。
	{
     
		for (int j = 1; j < n-i; j++)//这个循环只是将一个最大的数放到了最后面。
		{
     
			if (a[j - 1] > a[j])
			{
     
				Swap(&a[j - 1], &a[j]);
			}
		}
	}
}

void Swap(int* child, int* parent)
{
     
	int tmpt = *child;
	*child = *parent;
	*parent = tmpt;
}

可以进行优化：这样保证如果接近有序的时候可以更快的结束循环。

void BubbleSort(int* a, int n)
{
     
	for (int i = 0; i < n; i++)//将最大的数，次大的数一个一个的放在最后面。
	{
     
		int exchange = 0;
		for (int j = 1; j < n-i; j++)//这个循环只是将一个最大的数放到了最后面。
		{
     
			if (a[j - 1] > a[j])
			{
     
				Swap(&a[j - 1], &a[j]);
				exchange = 1;
			}
		}
		if (exchange == 0)
		{
     
			break;
		}
	}
}
void Swap(int* child, int* parent)
{
     
	int tmpt = *child;
	*child = *parent;
	*parent = tmpt;
}

（4）冒泡和直接插入相比较

直接插入更好。

如果在有序的情况下，都是O（n）

但是在接近有序的情况下，

1，2，3，5，4，6的情况下。

冒泡排序：（n-1）+（n-2）

直接插入排序：（n-1）+1

所以说直接插入排序对局部有序适应性更强。

所以直接插入排序在O（n^2）中算是比较牛的排序。

一般来说，如果比较随机的值，冒泡甚至都没有直接选择排序好。但是如果是比较有序的情况就比较好了。

（5）性能分析

a，空间复杂度：O（1），冒泡排序算法中有交换操作，需要用到一个辅助记录。

b，时间复杂度：显而易见O（n^2）。

最好情况：正序，只需要（n-1）+（n-2）次，时间复杂度是O（n）

最坏情况：逆序，总共要进行n-1趟冒泡排序，在第i趟排序中，比较次数为n-i，移动次数为3（n-i），所以经过计算加和之后就是O（n^2）。

c，算法稳定性：稳定，排升序，如果前一个数和后一个数相等，则不换，相对位置就没有发生改变，那么就十分的稳定。（可以人为的决定稳定性）

2，快速排序

（1）基本思想

它是冒泡排序的一种改进算法，快速排序采用了分治策略，即将原问题划分成若干个规模更小但与原问题相似的子问题，然后用递归方法解决这些子问题，最后再将他们组合成原问题的解。

（2）大体步骤

通过一趟排序，将待排序的记录分割成独立的两个部分，其中一部分的所有记录的关键值都比另一部分的所有记录关键值要小。然后再按此方法对这两部分记录分别进行快速排序，整个排序过程可以递归进行，以此达到整个记录序列变成有序。

（3）挖坑法快速排序

只需要设计代码完成一次单趟排序，然后进行递归就可以了。以下都是默认排升序

a 单趟排序

首先选一个关键字，（可以从数组开始选，可以从数组结尾选，也可以随机选。）

使用挖坑法，使得把这个关键字放在整个序列中间的位置，使得左边的数都比他要小，右边的数都比他要大。这样这个关键字以后不用动了。（单趟排序）

实际操作：

这是最开始的时候的序列。

6 1 2 7 9 3 4 5 10 8

一开始选一个key关键字，可以随便选，这里以6为例。然后设“前指针”begin指向6，“后指针”end指向8.（这个指针会随着程序的运行而移动）

将6保存到key中，然后6这个位置就为空，用X来表示。

X 1 2 7 9 3 4 5 10 8

然后end从右边往左边开始找比6小的，end–，找到5，然后将5放到X处，原来的5处就为空了。

变成：5 1 2 7 9 3 4 X 10 8

然后begin从左边往右边开始找比6大的，begin++，找到7，然后将7放到X处，原来的7处就为空了。

变成：5 1 2 X 9 3 4 7 10 8

然后end再从右边往左边开始找比6小的，end–，找到4，然后将4放到X处，原来的4处就为空了。

变成：5 1 2 4 9 3 X 7 10 8

然后begin从左边往右边开始找比6大的，begin++，找到9，然后将9放到X处，原来的9处就为空了。

变成：5 1 2 4 X 3 9 7 10 8

然后end再从右边往左边开始找比6小的，end–，找到3，然后将3放到X处，原来的3处就为空了。

变成：5 1 2 4 3 X 9 7 10 8

然后begin从左边往右边开始找比6大的，begin++，一直到end重合也没有找到，这个时候将key的值赋给X处。

最终变成：5 1 2 4 3 6 9 7 10 8

这样就完成了一个单趟，排好了一个数。

b代码实现

void QuickSort(int *a,int n)
{
     
	int begin = 0;
	int end = n - 1;
	int pivot = begin;//随便找一个坑
	int key = a[begin];//把这个关键字的值保存起来。
	while (begin < end)//这是单趟排序。
	{
     
		//右边找小放到左边
		while (begin < end && a[end]>=key)
		{
     
			--end;
		}
		//小的放在左边的空里，自己形成新的坑位。
		a[pivot] = a[end];
		pivot = end;
		//左边找大
		while (begin < end && a[begin] <= key)
		{
     
			begin++;
		}
		//大的放在右边的空里，自己形成新的坑位。
		a[pivot] = a[begin];
		pivot = begin;
	}
	//begin和end相遇了之后，就是最后那个关键字的位置。
	pivot = begin;
	a[pivot] = key;
}

c分治算法

这才排了一个数，还有其他的数要排，这个时候就用到了分治算法。

可以先判断key两边的序列是不是已经有序了，如果有序就停止，如果无序就分治。分治的话就需要用递归。

这样函数的参数就需要做一些改变。不能再传个数了，而是传两个参数，right和left。

就跟二叉树的遍历一样，先根，然后再左子树，然后再右子树。一直缩小到不可再再分割。当区间不存在的时候就是停止的时候。

把key左边的序列和key右边的序列拿出来，然后分别设置一个新的key值，再进行类似上面的挖坑法。

c-d补充三数取中

如果原序列有序，（无论顺序还是逆序）时间复杂度都是O（n^2），和直接插入一个样子的。这就是最坏的情况。

解决方法（官方）：三数取中法。就是左边，中间，右边三个数中选择大小中间的那个数作为key，这样就能避免有序导致的坏情况。

代码实现：

//三数取中
//选出三个数中，大小排在中间的那个数。
int GetMidIndex(int* a, int left, int right)
{
     
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
     
		if (a[mid] < a[right])
		{
     
			return mid;
		}
		else if (a[left] > a[right])
		{
     
			return left;
		}
		else
			return right;
	}
	else
	{
     
		if (a[left] < a[right])
		{
     
			return left;
		}
		else if (a[right] > a[mid])
		{
     
			return right;
		}
		else
			return mid;
	}
}

c-d补充小区间优化

继续优化：小区间优化（但效果不明显） 作用：就是减少递归次数的。
因为快排到最后就会有很多很多的序列，就要进行很多很多的递归，需要建立很多栈帧，调用函数。所以可以在序列足够小的时候使用直接插入排序，这样就避免了调用很多次的递归。
代码实现：

	if (pivot - 1 - left > 10)
	{
     
		QuickSort(a, left, pivot - 1);
	}
	else
	{
     
		InsertSort(a + left, pivot - 1 - left + 1);
	}
	if (right - pivot - 1 > 10)
	{
     
		QuickSort(a, pivot + 1, right);
	}
	else
	{
     
		InsertSort(a + pivot + 1,  right- pivot - 1+1);
	}

d优化后代码实现

void QuickSort(int* a, int left, int right)
{
     
	if (left >= right)//这就是两个停止条件，1，当left>right的时候就是区间不存在，2，left=right的时候就是只有一个数据。
	{
     
		return;
	}

	int index = GetMidIndex(a, left, right);//取三个数大小排在中间的那个数的下标，即中间数的下标。（这个是为了防止最坏的情况，即就是有序的时候）
	Swap(&a[left], &a[index]);//为了下面的逻辑不变，让这两个数交换，保证key还是序列首元素的前提下还是中间数。

	int begin = left;
	int end = right;
	int pivot = begin;//随便找一个坑
	int key = a[begin];//把这个关键字的值保存起来。
	while (begin < end)//这是单趟排序。
	{
     
		//右边找小放到左边
		while (begin < end && a[end] >= key)
		{
     
			--end;
		}
		//小的放在左边的空里，自己形成新的坑位。
		a[pivot] = a[end];
		pivot = end;
		//左边找大
		while (begin < end && a[begin] <= key)
		{
     
			begin++;
		}
		//大的放在右边的空里，自己形成新的坑位。
		a[pivot] = a[begin];
		pivot = begin;
	}
	//begin和end相遇了之后，就是最后那个关键字的位置。
	pivot = begin;
	a[pivot] = key;
	//这样进行完一遍之后就变成了：[left，pivote-1] pivot [pivot+1,right].
	//如果左子区间，和右子区间y有序，那么我们就有序了。利用分治算法递归。
    //第二次优化：小区间优化
	if (pivot - 1 - left > 10)
	{
     
		QuickSort(a, left, pivot - 1);
	}
	else
	{
     
		InsertSort(a + left, pivot - 1 - left + 1);
	}
	if (right - pivot - 1 > 10)
	{
     
		QuickSort(a, pivot + 1, right);
	}
	else
	{
     
		InsertSort(a + pivot + 1,  right- pivot - 1+1);
	}

（4）左右指针法快速排序

a理论

让begin指向前面，让end指向后面

然后选中6为key，然后从end8开始往前找比key小的，（找到了5），然后从begin6开始往后找比key大的，（找到了7），然后将他俩交换。依次类推，直到begin和end重合在3处，然后将6和3交换一下就完成了。

最后：

3，1，2，5，4，6，9，7，10，8

这个结果与挖坑法最后的结果不是一样的。

挖坑法最后的结果是：

5，1，2，4，3，6，9，7，10，8

b代码实现

//挖坑法的变形
//左右指针法
void PartSort2(int* a, int left, int right)
{
     
	int index = GetMidIndex(a, left, right);//这是防止最坏的情况产生，即有序的情况。
	Swap(&a[left], &a[index]);

	int begin = left, end = right;
	int keyi = begin;
	while(begin<end)
	{
     
		while (begin < end && a[end] >= a[keyi])//找小的//这里应该是要有=的，不然就走可能死循环，走不动了。如果没有等号，在a[begin] = a[end] = a[keyi]的时候就会停住了，进行交换之后也没有办法继续进行循环了。
		{
     
			end--;
		}
		while (begin < end && a[begin] <= a[keyi])//找大的
		{
     
			begin++;
		}
		Swap(&a[begin], &a[end]);

	}
	Swap(&a[begin], &a[keyi]);
	int KeyIndex = end;//这里赋end还是begin都是一样的。
	//分成了：[left，KeyIndex] KeyIndex [KeyIndex+1,right]。

	if (KeyIndex - 1 - left > 10)
	{
     
		QuickSort(a, left, KeyIndex - 1);
	}
	else
	{
     
		InsertSort(a + left, KeyIndex - 1 - left + 1);
	}
	if (right - KeyIndex - 1 > 10)
	{
     
		QuickSort(a, KeyIndex + 1, right);
	}
	else
	{
     
		InsertSort(a + KeyIndex + 1, right - KeyIndex - 1 + 1);
	}

}

（5）前后指针法快速排序

a理论

这个方法也是要找两个指针，一个设成是prev，另一个设成事cur，让prev指向最前面的数，也就是6，让cur指向prev后面的数，也就是1。将开始的6设置成key值。

运行步骤：cur不断向右走去找比key（6）小的值，如果找到了就停下来，++prev，然后交换prev和cur位置的值。

以上面的序列为例子：

key是6，prev指向6，cur指向1，cur的值比key小，停下来，然后++prev，prev现在指向了1，然后交换cur和prev（这时候cur和prev都是1，交换也没有变化），然后cur向右走，指向了2，cur的值再次比key小，然后++prev，prev现在指向了2，然后交换cur和prev（这时候cur和prev都是2，交换也没有变化），然后cur向右走，cur指向了7，大于key，所以继续向右走，cur指向9，大于key，所以继续向右走，cur指向了3，小于key，所以++prev，prev指向了7，然后交换cur和prev的数值.
序列变成：6，1，2，3，9，7，4，5，10，8.（这个时候）

cur继续向右走，cur指向了4，小于key，所以++prev，prev指向了9，然后交换cur和prev的数值.
序列变成：6，1，2，3，4，7，9，5，10，8.

cur继续向右走，cur指向了5，小于key，所以++prev，prev指向了7，然后交换cur和prev的数值.
序列变成：6，1，2，3，4，5，9，7，10，8.

cur继续向右走，cur指向了10，cur大于key，继续向右走，cur指向了8，cur大于key，继续向右走，走出去了，然后将prev指向的位置和key指向的位置进行交换。

最后变成了：

5，1，2，3，4，6，9，7，10，8.

（总体的思路还是找小的，两指针中间间隔的都是比key大的，找到小的以后就和大的进行交换，相当于把小的往左边送，把大的往右边送。）

b代码实现

//第三种快速排序的方法（最不容易出错，但是也是最抽象的方法）
//前后指针法
void PartSort3(int* a, int left, int right)
{
     
	int index = GetMidIndex(a, left, right);//这是防止最坏的情况产生，即有序的情况。//三数取中法
	Swap(&a[left], &a[index]);
	int keyi = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
     
		if (a[cur] < a[keyi])
		{
     
			prev++;
			Swap(&a[prev], &a[cur]);
		}
		++cur;
	}
	Swap(&a[keyi] , &a[prev]);
	int KeyIndex = prev;//这里赋end还是begin都是一样的。
	//分成了：[left，KeyIndex] KeyIndex [KeyIndex+1,right]。

	if (KeyIndex - 1 - left > 10)
	{
     
		QuickSort(a, left, KeyIndex - 1);
	}
	else
	{
     
		InsertSort(a + left, KeyIndex - 1 - left + 1);
	}
	if (right - KeyIndex - 1 > 10)
	{
     
		QuickSort(a, KeyIndex + 1, right);
	}
	else
	{
     
		InsertSort(a + KeyIndex + 1, right - KeyIndex - 1 + 1);
	}
}

（5）性能分析

a，空间复杂度：O（n），快速排序在系统内部需要一个栈来实现递归，每层递归调用时的指针和参数均需要用栈来存放。快速排序的递归过程可用一棵二叉树来表示，若每次划分比较均匀，则递归树的高度为O（logn），顾所需栈空间为O（logn），最坏的情况下，递归树是一个单枝树，树的高度为O（n）时，所需栈空间也是O（n）。

b，时间复杂度：O（n*logn）。单趟的是O（n），就是两个指针往中间走，一直到重合，肯定是O（n）

联想二叉树的结构，一共有n个元素要排，每一次单趟走完之后就相当于构建了一个二叉树的新层。n个元素需要构建logn层。

所以快速排序的时间复杂度就是O（n*logn）。

c，算法稳定性：不稳定。不好控制。交换位置的时候相同的数字是不好控制放在同一边的。

四，归并排序

归并排序

（1）基本思想

将一个序列分成左半区间和右半区间。使得左半区间和右半区间分别有序。

然后进行归并，创建一个新的数组，然后对两个区间取小的放到新的数组当中。然后再把这个新的数组拷贝到原先的数组当中。

那怎么让左半区间和右半区间有序呢？分治思想。一半分解，一半合并。

（2）主要步骤

（3）代码实现

void _MergeSort(int* a, int left,int right,int* tmp)
{
     
	if (left >= right)//如果错位或者序列中就一个数据了，就直接return，错位一般不会遇见的（离谱）
	{
     
		return;
	}
	int mid = (left + right) >> 1;//相当于除2.
	//这样就可以分成两部分了。[left,mid] [mid+1,right]
	//如果这两部分都是有序的了，那么就可以归并他们了（区间中只包含一个数就算是有序）。

	_MergeSort(a, left,mid,tmp);//让左边有序
	_MergeSort(a, mid+1, right,tmp);//让右边有序

	//结束分解以后，就开始归并。
	int begin1 = left, end1 = mid;     //定义下新变量
	int begin2 = mid+1, end2 = right;
	int index = left;//代表每个小区间的第一个数据
	while ((begin1 <= end1) && (begin2 <= end2))//向新数组中放数据
	{
     
		if (a[begin1] < a[begin2])
		{
     
			tmp[index++] = a[begin1++];
		}
		else
		{
     
			tmp[index++] = a[begin2++];
		}	
	}
	while (begin1 <= end1)//区域1剩余的放进数组。
	{
     
		tmp[index++] = a[begin1++];
	}
	while (begin2 <= end2)//区域2剩余的放进数组
	{
     
		tmp[index++] = a[begin2++];
	}
	//将新的数组拷贝到原来的数组中。
	for (int i = left; i <= right; i++)
	{
     
		a[i] = tmp[i];
	}
}

void MergeSort(int* a,int n)
{
     
	int* tmp = (int*)malloc(sizeof(int) * n);//有空间的消耗了，空间复杂度提升。O(n)
	//接下来就要进行分治递归了，但是如果自己递归自己的话，每一次调用自己都会malloc一次空间，所以考虑使用子函数，然后子函数调用自己。
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

（4）性能分析

a，空间复杂度：O（n），归并排序需要一个与待排序记录序列等长的辅助数组来存放排序过程中的中间结果。

b，时间复杂度：O（n *
logn），时间复杂度等于归并趟数与每一趟时间复杂度的成绩。归并趟数是logn，由于每一趟归并就是将两两有序序列归并，而每一对有序序列归并时，记录的比较次数均不大于记录的移动次数，而记录的移动次数等于这一对有序序列的长度之和，所以每一趟归并的移动次数等于数组中记录的个数n。所以每一趟归并的时间复杂度O（n），所以相乘就是O（n*logn）。

c，算法稳定性：稳定（可以控制），归并的时候可以人为的规定让第一组的相同的数组先进入新空间。

（5）外号（外排序）

假设10G的数据放到硬盘的文件中，内存是不够的，只有1G的内存可用。要排序，如何排呢？

之前的那些排序（都是内排序）是没法用的，因为排序是需要先把数据保存在内存中的，但是电脑的内存一共才4G左右，肯定不够10G.这就需要在磁盘中进行排序。需要依靠归并排序了归并排序既可以在内存中进行排序，也可以在文件中排序。

解决：

10G的文件，，切分成10个1G的文件，并且让这10个1G的文件有序。依次读文件，每次读1G到内存的一个数组中，用快速排序对其排序，使其有序，然后再写到一个文件中，再继续读下一个1G的数据（直接覆盖掉刚才的文件）对这10个1G的文件进行编号，1到10.这个时候就可以对这10个文件进行归并了，两两归并，再四四归并等。（这个归并过程就不能借助内存了，只能在硬盘当中归并）。1G和1G归并，2G和2G归并，4G和4G归并，8G和2G归并，到10G.

归并排序的思想就是借助一个新空间，然后对文件进行归并。两个文件都拿出一个最小的进行比较，将相对小的放进心的大文件中。依次往后，直到其中的一个文件读完，最后把另一个文件剩余的部分也加进新的大文件中。

1 1 1 1 1 1 1 1 1 1

2 2 2 2 2

4 4 2

8 2

10

为什么之前的快速排序等不能在磁盘中排序呢？

因为磁盘中（文件中）读数据只能一个一个依次的读，快排等是从两边往中间走等（需要借助指针等辅助）。

所以只有归并排序才能实现。

✨排序总结✨

综合比较

前三种排序方式，插入排序比较好一点。（它最好的情况是O（n））

后四种排序方式，快速排序比较好一点。

（堆排序上来得建堆，建完堆之后才开始排序，不及快速排序）

（归并排序右空间的消耗O(n)）

（快排虽然最坏的情况是O（n^2），但是经过使用三数取中选key，基本不会出现最坏的情况。）

稳定性比较

比如数组：1，2，1

如果第一个1和第二个1的相对位置不变（即第一个1一直在第二个前面），那么他们就很稳定。

1，冒泡排序：稳定，排升序，如果前一个数和

后一个数相等，则不换，相对位置就没有发生改变，那么就十分的稳定。（可以人为的决定稳定性）

2，选择排序：不稳定。虽然可以人为地控制相同的数字谁在前谁在后，但是在换位置的时候可能会影响其他的相同数字的相对位置。

3，插入排序：稳定。如果我比你小才把你向后挪，我自己往前挪，相等的时候可以不动，相对位置不变。

4，希尔排序：不稳定，它会分组，预排序的时候，如果把相同的数分到了不同的组里，相对顺序就不可控了。

5，堆排序：不稳定，在建好堆以后数会进行交换，会影响相对位置。

6，归并排序：稳定（可以控制），归并的时候可以人为的规定让第一组的相同的数组先进入新空间。

7，快速排序：不稳定。不好控制。交换位置的时候相同的数字是不好控制放在同一边的。

---

觉得对自己有帮助的小伙伴可以点个赞哈，欢迎大家在评论区一起交流哦。