OpenCV学习——轮廓检测
前言
轮廓检测是传统视觉中非常常用的功能,这里简单记录一下opencv中的轮廓检测算法使用方法,至于理论,后续有机会再去细品。
国际惯例:
OpenCV官方的轮廓检测教程python版
OpenCV中的二值化方法教程
OpenCV轮廓层级官方文档
维基百科:图像矩(Image Moment)
调用流程和方法
OpenCV里面通常要求是针对二值图像进行二值化,所以轮廓检测包含如下步骤:
- 载入图像
- 灰度化
- 二值化
- 轮廓检测
代码实现如下:
img =cv2.imread("blackBG.jpg")
# grayscale
# https://docs.opencv.org/4.5.0/d7/d4d/tutorial_py_thresholding.html
gray_img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret,bin_img = cv2.threshold(gray_img,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
二值化
注意二值化方法,这里使用的是threshold函数,它的第三个参数代表的意义可以查询此处的官方文档,这里将方法截图贴出来
其实除了threshold还有一个adaptiveThreshold函数可以做二值化,调用方法:
#dst=cv.adaptiveThreshold(src,maxValue,adaptiveMethod,thresholdType,blockSize,C[, dst])
bin_img1 = cv.adaptiveThreshold(img,255,cv.ADAPTIVE_THRESH_MEAN_C,\
cv.THRESH_BINARY,11,2)
bin_img2 = cv.adaptiveThreshold(img,255,cv.ADAPTIVE_THRESH_GAUSSIAN_C,\
cv.THRESH_BINARY,11,2)
从第三个参数可以发现也有两个二值化方法:
ADAPTIVE_THRESH_MEAN_C:阈值是每个像素邻域区域的均值减去常量CADAPTIVE_THRESH_GAUSSIAN_C::阈值是每个像素相邻域区域的高斯加权和减去常量C
轮廓检测
python的调用方法如下:
contours, hierarchy =cv.findContours(image,mode,method[,contours[, hierarchy[, offset]]])
返回的参数
contours:检测到的轮廓,每个轮廓是由一些点构成的向量组成hierarchy:记录轮廓之间的关系,四个维度分别代表:同级后一个轮廓的序号、同级上一个轮廓的序号、第一个孩子序号,父亲序号
第二个数参数mode是检测轮廓的层级关系排列规则:
RETR_EXTERNAL:仅仅检测外圈轮廓RETR_LIST:检测所有轮廓,但是没有层级关系RETR_CCOMP:仅仅两层包含关系,即只有外层和内层,假设有夹层,那么夹层也算外层,只要某个轮廓还包含有轮廓,都算外部轮廓RETR_TREE:检测所有的轮廓,并建议非常完整的层级关系RETR_FLOODFILL:无描述
第三个参数method是轮廓点的存储方式:
CHAIN_APPROX_NONE:相邻的轮廓点坐标只相差一个像素,所以是连续轮廓点CHAIN_APPROX_SIMPLE:横、竖、对角线段只保存断点数据,比如矩形就只保存四个顶点。- 还有两种没做过多叙述:
CHAIN_APPROX_TC89_L1和CHAIN_APPROX_TC89_KCOS是Teh-Chin chain近似算法里面采取的两种表示
画图函数
就一个函数drawContours,调用方法如下:
image=cv.drawContours(image, contours, contourIdx, color[, thickness[, lineType[, hierarchy[, maxLevel[, offset]]]]] )
输入参数:
contours:是list类型的数组,里面存储了很多array数组去代表各个轮廓contourIdx:从上面的轮廓list中取出哪一个画出来,-1代表全部color:线条颜色thickness:线条粗细,-1代表填充式画轮廓,整个轮廓内部被指定颜色填充lineType:线条类型,虚线、实线之类的
【注意】如果将原图传入画图函数,这个原图会被画上轮廓,所以画图时候最好建立一个副本,在副本上画图。
轮廓检测函数验证
主要验证检测时的层级结构和记录关键点的方式,也就是第2和3个参数。
检测黑色还是白色边界
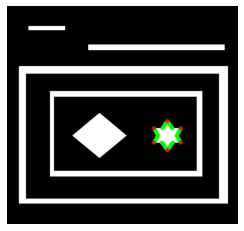
黑色背景图,以下图为例
先检测所有的轮廓并且画出来
img =cv2.imread("blackBG.jpg")
gray_img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret,bin_img = cv2.threshold(gray_img,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
cv2.drawContours(img,contours,-1,(0,255,0),5)
plt.imshow(img[...,::-1])
plt.axis('off')
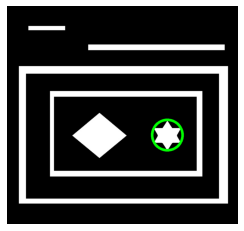
白色背景图以下图左为例,同时以同样的代码尽心轮廓检测,轮廓图为下图右:
结论:检测白色背景的图片,会有一个和图像宽高相等的轮廓,而黑色区域没有;所以轮廓检测是针对白色区域的边缘进行的,这个和图像等宽高的轮廓经常会影响一些逻辑的书写。
层级关系
-
RETR_EXTERNAL:仅外圈轮廓# RETR_EXTERNAL:仅外圈轮廓 contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE) cv2.drawContours(img,contours,-1,(0,255,0),5) plt.imshow(img[...,::-1]) plt.axis('off') print(hierarchy) ''' [[[ 1 -1 -1 -1] [ 2 0 -1 -1] [-1 1 -1 -1]]] '''
从轮廓图可以发现,仅仅只有确定为最外圈的轮廓被画出来,而且输出的hierarchy数组可以发现,前两列分别代表当前层级当前轮廓的下一个轮廓和上一个轮廓索引,而后两列分别代表当前层级的子层级的第一个轮廓索引和父层级的轮廓索引,因为RETR_EXTERNAL只提取最外层轮廓,所以上下层级都是-1
-
RETR_LIST:所有轮廓都包含,但是没有层级关系# RETR_EXTERNAL:全部轮廓,无层级关系 contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE) cv2.drawContours(img,contours,-1,(0,255,0),5) plt.imshow(img[...,::-1]) plt.axis('off') print(hierarchy) ''' [[[ 1 -1 -1 -1] [ 2 0 -1 -1] [ 3 1 -1 -1] [ 4 2 -1 -1] [ 5 3 -1 -1] [ 6 4 -1 -1] [ 7 5 -1 -1] [-1 6 -1 -1]]] '''
代表当前层级父子层级的后两个维度依旧为-1,但是轮廓全部都提取出来了。
-
RETR_CCOMP:仅仅两层关系,是否为内层或者是否为外层,而且这个内层一定是这个外层的洞,这个洞的定义指内外层组合构成一片白色区域。如下图代码测试# RETR_CCOMP:全部轮廓,只有两种层级关系 contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_CCOMP, cv2.CHAIN_APPROX_SIMPLE) img_show = img.copy() for i in range(len(contours)): if(hierarchy[0,i,3]!=-1): cv2.drawContours(img_show,contours,i,colormap[i],5) cv2.drawContours(img_show,contours,hierarchy[0,i,3],colormap[i],5) plt.imshow(img_show[...,::-1]) plt.axis('off') print(hierarchy) # 红:0 橙;1 黄:2 绿:3 青:4 蓝:5 紫:6 灰:7 ''' [[ 1 -1 -1 -1] [ 2 0 -1 -1] [ 4 1 3 -1] [-1 -1 -1 2] [ 6 2 5 -1] [-1 -1 -1 4] [ 7 4 -1 -1] [-1 6 -1 -1]]] '''上述代码表示将当前轮廓与其父轮廓用同色画出来:
可以发现四个轮廓组成的两个白色区域被显示出来,绿色区域为3号轮廓,从hierarchy中找到3号轮廓的结构为[-1 -1 -1 2],自行可视化可以发现这个3号轮廓是白色区域中最内层的那个轮廓,而其父亲索引为2,轮廓2的结构为[ 4 1 3 -1],可以发现它的第一个孩子是3,而由于是外轮廓(不管是否为最外圈),所以父亲索引为-1。其余轮廓同理分析。
【注】这个轮廓结构有点绕,但是只需要记住只有内、外轮廓,只要当前轮廓有内轮廓一起组成白色区域,那么这个轮廓就是外轮廓,不管它在不在其它轮廓内部
可视化时候本来用当前轮廓和子轮廓来显示,但是想到hierarchy只记录第一个子轮廓,当时差点以为组成“洞”的只可能有两个轮廓,也就是一个轮廓有且只可能有一个子轮廓,但是发现问题,一个轮廓可能会有两个子轮廓,所以必须用当前轮廓与父轮廓可视化,而不是当前轮廓和子轮廓可视化,比如下面这个图,及其对应的轮廓图和层级关系:
轮廓对应顺序分别是红、橙、黄,其CCOMP层级关系为:
[[[-1 -1 1 -1]
[ 2 -1 -1 0]
[-1 1 -1 0]]]
可以发现,内部两个轮廓的父亲都是0,证明这个洞是由三个轮廓组成的。
-
RETR_TREE:这个是非常严谨的表达轮廓间层级关系的参数
直接输出hierarchy看看:contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE) print(hierarchy) # 红:0 橙;1 黄:2 绿:3 青:4 蓝:5 紫:6 灰:7 ''' [[[ 6 -1 1 -1] [-1 -1 2 0] [-1 -1 3 1] [-1 -1 4 2] [ 5 -1 -1 3] [-1 4 -1 3] [ 7 0 -1 -1] [-1 6 -1 -1]]] '''真正的由外向内,一层一层的编号;是
CCOMP的更进一步细化,如果CCOMP中构成洞的两个轮廓的外轮廓在其它轮廓内部,那么就是从其它轮廓编号继续编号,即洞的外轮廓的父亲是包含它的紧邻着的轮廓编号。通过判断父亲是否相同,将轮廓按照层级画出来
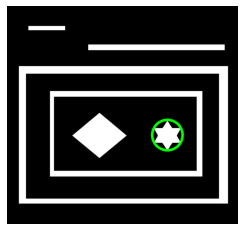
img_show = img.copy() for i in range(len(contours)): cv2.drawContours(img_show,contours,i,colormap[hierarchy[0,i,3]+1],5) plt.imshow(img_show[...,::-1]) plt.axis('off')
可以发现,红色部分就是最外圈轮廓,父亲为-1;而最内部的青色(菱形、六角星)的孩子是-1,父亲是绿色的轮廓3。
存储方法
CHAIN_APPROX_NONE和CHAIN_APPROX_SIMPLE的区别就在于轮廓为线段的部分,是否仅存储端点坐标。
比如上述图片的最外层的矩形轮廓,分别使用两种存储参数去存储轮廓点的值:
使用SIMPLE只保存端点
contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
img_show = img.copy()
cnt_idx = 0
cnt = contours[cnt_idx]
for i in range(cnt.shape[0]):
cv2.circle(img_show,(cnt[i,0,0],cnt[i,0,1]),5,(0,255,0),5)
plt.imshow(img_show[...,::-1])
使用NONE按像素保存
contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
img_show = img.copy()
cnt_idx = 0
cnt = contours[cnt_idx]
for i in range(cnt.shape[0]):
cv2.circle(img_show,(cnt[i,0,0],cnt[i,0,1]),5,(0,255,0),5)
plt.imshow(img_show[...,::-1])
轮廓的其它特征和属性
包括轮廓的图像矩、面积、周长、多边形逼近、外接凸多边形、凸性判断、外接矩形、外接圆、外接椭圆、直线拟合。
图像矩
维基百科中的解释是:指图像的某些特定像素灰度的加权平均值,或者是图像具有类似功能或意义的属性。可以通过图像的矩来获得图像的部分性质,包括面积(或总体亮度),以及有关几何中心和方向的信息。它可以被用来获得相对于特定变换的不变性(平移、缩放、旋转不变性) 。具体可查阅维基百科中图像矩的描述,这里列一下矩的计算方法:
-
对于二维连续函数 f ( x , y ) f(x,y) f(x,y), ( p + q ) (p+q) (p+q)阶的矩被定义为:
M p q = ∫ − ∞ ∞ ∫ − ∞ ∞ x p y q f ( x , y ) d x d y M_{pq}=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}x^py^qf(x,y)dxdy Mpq=∫−∞∞∫−∞∞xpyqf(x,y)dxdy -
对于灰度图像的像素强度 I ( x , y ) I(x,y) I(x,y),原始图像的矩 M i j M_{ij} Mij计算方法:
M i j = ∑ x ∑ y x i y i I ( x , y ) M_{ij}=\sum_x\sum_yx^iy^iI(x,y) Mij=x∑y∑xiyiI(x,y) -
原始矩包含以下的一些的有关原始图像属性的信息:
- 二值图像的面积或灰度图像的像素总和,可以表示为 M 00 M_{00} M00
- 图像的几何中心可以表示为 { x ˉ , y ˉ } = { M 10 M 00 , M 01 M 00 } \{\bar x,\bar y\}= \{\frac{M_{10}}{M_{00}},\frac{M_{01}}{M_{00}}\} { xˉ,yˉ}={ M00M10,M00M01}
在OpenCV中的表示为:
cnt = contours[0]
M = cv.moments(cnt)
中心为:
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])
轮廓面积和周长
获取指定轮廓所包含的面积
area = cv.contourArea(cnt)
获取指定轮廓所包含的周长,第二个参数指示当前输入为闭合轮廓(true)还是非闭合曲线(false)
perimeter = cv.arcLength(cnt,True)
轮廓多边形逼近
通过具有更少轮廓点的形状在允许误差范围内逼近指定轮廓,比如你提取一个矩形,但是有锯齿导致轮廓不是矩形,可以使用此功能将矩形近似逼近出来
epsilon = 0.1*cv.arcLength(cnt,True)
approx = cv.approxPolyDP(cnt,epsilon,True)
这个意思就是新的轮廓的周长和原始轮廓周长的误差范围在原周长的十分之一以内。
比如最开始的例子中,最内部的六角星的轮廓点并不是规整的五角星轮廓,也就是说使用SIMPLE存储的时候不是存的每条边的端点。
下图就是使用这个逼近函数去找到端点的结果:
contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
img_show = img.copy()
cnt_idx = 4
cnt = contours[cnt_idx]
for i in range(cnt.shape[0]):
cv2.circle(img_show,(cnt[i,0,0],cnt[i,0,1]),5,(0,255,0),5)
epsilon = 0.1*cv2.arcLength(cnt,True)
approx = cv2.approxPolyDP(cnt,epsilon,True)
for i in range(approx.shape[0]):
cv2.circle(img_show,(approx[i,0,0],approx[i,0,1]),5,(0,0,255),5)
plt.imshow(img_show[...,::-1])
plt.axis('off')
绿色为原始轮廓点,红色为逼近后的轮廓点,可以发现六角星的所有边的顶点都保存了
轮廓凸多边形逼近
上面的多边形逼近不管简化的轮廓是否为凸的,所以又提供了一个检测凸多边形逼近的函数
hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]
输入分别为:轮廓点、输出(不管这个参数)、顺时针(true)/逆时针(false)、返回多边形坐标在原轮廓点序中的索引(False)/直接返回坐标(true)
还是那个六角星:
contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
img_show = img.copy()
cnt_idx = 4
cnt = contours[cnt_idx]
for i in range(cnt.shape[0]):
cv2.circle(img_show,(cnt[i,0,0],cnt[i,0,1]),5,(0,255,0),5)
approx = cv2.convexHull(cnt)
for i in range(approx.shape[0]):
cv2.circle(img_show,(approx[i,0,0],approx[i,0,1]),5,(0,0,255),5)
plt.imshow(img_show[...,::-1])
plt.axis('off')
绿色为原始轮廓点,红色为凸多边形逼近后的轮廓点,可以发现比多边形逼近函数的结果少了内凹角顶点。
凸性检测
如何判断一个轮廓是否为凸的,有一个函数k = cv.isContourConvex(cnt),返回true就是凸的。
OpenCV对这个凸多边形还提供了提取更详细信息的函数convexityDefects,用于获取凸多边形和轮廓之间的关系:
void convexityDefects(InputArray contour, InputArray convexhull, OutputArrayconvexityDefects)
输入:原始轮廓点、凸多边形顶点对应原轮廓中的索引、输出(不管)
所以针对那个五角星的调用方法是:
contours, hierarchy = cv2.findContours(bin_img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
cnt_idx = 4
cnt = contours[cnt_idx]
approx = cv2.convexHull(cnt,returnPoints=False)#使用false获取多边形顶点索引
print(cv2.convexityDefects(cnt,approx))
'''
[[[ 321 0 357 4403]]
[[ 0 67 31 4403]]
[[ 67 128 96 4230]]
[[ 128 194 163 4223]]
[[ 194 260 225 4223]]
[[ 260 321 292 4230]]]
'''
得到了和多边形逼近线段个数相同行的列为4的矩阵,分别代表:起始点索引、结束点索引、当前线段截取的轮廓点中距离线段最远的点索引、这个最远点与当前线段的距离
验证一下,把第三个维度,也就是距离每条边最远的轮廓点画出来:
边界框
分为矩形、圆形边界
-
矩形:不考虑形状的旋转,获取直边界矩形
x,y,w,h = cv2.boundingRect(cnt) -
矩形考虑旋转,获取最小的外接矩形
rect = cv2.minAreaRect(cnt) box = cv2.boxPoints(rect) box = np.int0(box)
画图看看区别,直边界用绿色,最小外接矩形用红色
img_show = img.copy()
#无旋转矩形
cv2.rectangle(img_show,(x,y),(x+w,y+h),(0,255,0),4)
#有旋转矩形
cv2.drawContours(img_show,[box],0,(0,0,255),4)
plt.imshow(img_show[...,::-1])
plt.axis('off')
外接圆:minEnclosingCircle
# 最小外接圆
(x,y),radius = cv2.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
img_show = img.copy()
cv2.circle(img,center,radius,(0,255,0),10)
plt.imshow(img_show[...,::-1])
plt.axis('off')
形状拟合
包括椭圆、直线拟合
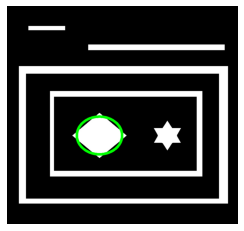
椭圆拟合:fitEllipse,将里面的那个菱形拟合
# 椭圆拟合
ellipse = cv2.fitEllipse(contours[5])
img_show = img.copy()
cv2.ellipse(img_show,ellipse,(0,255,0),10)
plt.imshow(img_show[...,::-1])
plt.axis('off')
直线拟合:fitLine,使得当前轮廓所有点与直线距离和最短
rows,cols = img.shape[:2]
[vx,vy,x,y] = cv2.fitLine(cnt, cv2.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
img_show = img.copy()
cv2.line(img_show,(cols-1,righty),(0,lefty),(0,255,0),2)
plt.imshow(img_show[...,::-1])
plt.axis('off')
点与轮廓的关系
通过pointPolygonTest函数判断某个点是否在轮廓内部后者外部,然后返回距离轮廓的最短距离
retval=cv.pointPolygonTest(contour,pt,measureDist)
输入分别为:轮廓、某个点、是否返回距离;如果仅仅需要判断点是否再轮廓内部,第三个参数设置False,在内部为+1,外部为-1,在轮廓上为0。
形状匹配
可以利用matchShapes输入两个轮廓,计算相似度,得分越低越相似
retval = cv.matchShapes( contour1, contour2, method, parameter )
输入为:第一个形状的轮廓、第二给形状的轮廓、匹配算法、参数(暂不支持,不管)
匹配算法是基于图像的Hu矩,计算方法为:
m i = s i g n ( h i ) ⋅ log h i m_i = sign(h_i)\cdot \log h_i mi=sign(hi)⋅loghi
其中 h i h_i hi代表Hu矩。
匹配算法分为:
使用案例,先构建一些图像,然后计算相似度:
img1 = cv2.imread('shape1.png',0)
img2 = cv2.imread('shape2.png',0)
img3 = cv2.imread('shape3.png',0)
ret, thresh = cv2.threshold(img1, 127, 255,0)
ret, thresh2 = cv2.threshold(img2, 127, 255,0)
ret, thresh3 = cv2.threshold(img3, 127, 255,0)
contours,hierarchy = cv2.findContours(thresh,2,1)
cnt1 = contours[0]
contours,hierarchy = cv2.findContours(thresh2,2,1)
cnt2 = contours[0]
contours,hierarchy = cv2.findContours(thresh3,2,1)
cnt3 = contours[0]
ret1 = cv2.matchShapes(cnt1,cnt2,1,0.0)
ret2 = cv2.matchShapes(cnt1,cnt3,1,0.0)
print( ret1,ret2 )
plt.subplot(131)
plt.imshow(img1,cmap='gray')
plt.axis('off')
plt.subplot(132)
plt.imshow(img2,cmap='gray')
plt.axis('off')
plt.subplot(133)
plt.imshow(img3,cmap='gray')
plt.axis('off')
'''
0.14475720763533126 0.3168697153308031
'''
可以发现形状1和2的非常接近,一个四角星一个五角星,他俩得分很低,越相似。
其它属性
-
获取掩膜(
mask)mask = np.zeros(gray_img.shape,np.uint8) cv2.drawContours(mask,[cnt],0,255,-1) pixelpoints = np.transpose(np.nonzero(mask)) #pixelpoints = cv.findNonZero(mask) plt.imshow(mask,cmap='gray')
注意使用可以使用numpy或者OpenCV去查找到掩膜内所有像素坐标,但是他俩的位置不一样,因此numpy的坐标需要转置才能与OpenCV保持一致,列是x,行是y
-
获取局部最大值、最小值级它们的位置
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(imgray,mask = mask)注意第一个参数必须是单通道的图,第二个参数可有可无,用于选择特定区域。
这个在
Openpose中,从每个关节的特征图中提取关节坐标用到过,具体可看之前解析OpenPose的文章。 -
均值:通道分开
mean_val = cv.mean(im,mask = mask)
后记
图像处理经常遇到轮廓相关的问题,比如二维码检测定位之类的大都是用二维码四个角的定位符和矫正符的比例特征来定位。这里对官方的教程做了简单的综合整理。
完整的python脚本实现放在微信公众号的简介中描述的github中,有兴趣可以去找找,同时文章也同步到微信公众号中,有疑问或者兴趣欢迎公众号私信。