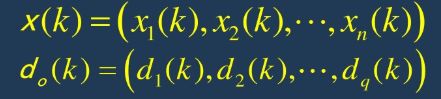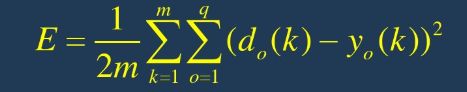机器学习——神经网络（四）：BP神经网络

BP神经网络（Back Propagation）

  误差逆传播算法（error Back Propagation 简称BP），实际上是多层感知器的一种,在1986由Rumelhart和Hinton为首的科学小组提出。BP神经网络具有任意复杂的模式分类能力和优良的多维函数映射能力，解决了简单感知器不能解决的异或问题和其他问题。从结构而言具有输入层、隐含层和输出层；从本质上来讲是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值。

BP神经网络结构

1. 主要过程

• (1)工作信号向前正向传播的子过程
• (2)误差信号反向传播向后反馈的子过程
  借用一个例子BP（Back Propagation）神经网络学习笔记：我要追求女神，那我总得表示一下吧！于是我给她买花，讨她欢心。然后，她给我一些表示（或者叫暗示），根据这个表示，与我最终目的进行对比（追求到女神），然后我进行调整继续表示，一直循环往复，直到实现最终目的——成功最求到女神。我的表示就是“信号前向传播”，女神的表示就是“误差反向传播”。这就是BP神经网络的核心。

• 其中主要的过程是：
  正向传播获得输出结果

Created with Raphaël 2.2.0 输入层 隐藏层 输出层

BP正向传播

最小二乘、梯度下降等方法进行对比标签和输出，逐层向上反馈其结果误差，更新权值

Created with Raphaël 2.2.0 输出层 隐藏层 输入层

BP反馈反向传播

2.整体思路

• 学习目的：

得到一个模型，当输入一组新的数据可以输出我们所期望的数据

• 学习方式：

输入样本数据经过激活函数的处理得到输出，输出与已知标签对比，反向改变权值。

• 学习本质：

对各种连接权值进行动态调整

• 学习核心：

权值的调整（在学习过程中对各个神经元的连接权进行的一定的调整规则）

3. 算法详解

  神经网络模拟生物的神经结构与活动，构造分类器。基本组成单位为神经元，当输入神经元的参量大于某一个阈值的时候，神经元变为兴奋状态，产生输出，否则不响应。这个输入与其相连接的所有神经元都有关系，神经元的响应函数可以分为多种不同形式的（即激活函数）。
下面介绍一下：

1. 激活函数
2. BP推导

1）激活函数

定义：神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性值直接传递给下一层（隐层或输出层）。在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数（又称激励函数）。

应用原因：不使用激活函数($f(x)=x$)，每一层节点的输入就是上层输出的线性函数，无论多少层隐含层，最终输出的结果都是输入的线性组合，相当于最原始的感知机，网络的逼近能力非常有限。

常用激活函数及其特点：

（1）sigmoid函数
非线性激活函数，其数学公式为：
$$f(z)=\frac{1}{1+e^{-z}}$$
几何图像为：

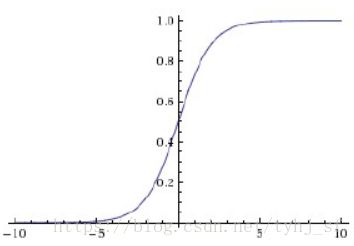sigmoid 函数及其导数图像

特点：

可将输入的连续值转变为0和1之间的输出，如果是非常小的负数输出为0，非常大的正数输出为1

缺点：

• 在深度神经网络中梯度反向传播时导致梯度爆炸和梯度消失
• sigmoid的输出output不是0均值（zero-centerd）
• 解析式中含有幂运算，计算求解的代价较高，对于大规模的机器学习算法和训练过程对时间空间的消耗较高

（2）tanh函数
函数解析式：
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
tanh函数及其导数图像

tanh 函数及其导数图像

优点：

• 解决了Sigmoid函数不是zero-centered输出的问题

不足：

• 梯度消失和幂运算的问题仍然存在

（3）Relu函数
Relu函数解析式
$$Relu=max(0,x)$$
Relu函数及其导数图像

Relu 函数及其导数图像

描述 >Relus是一个取最大值的函数，函数并非是全区间可导的

优点

• 解决了梯度消失（gradient vanishing）的问题（在正区间）
• 不含有幂指数计算，计算速度快
• 收敛速度较快

注意问题：

• Relu的输出不是zero-centered的值
• Deep ReLU Problem,即有的神经元可能永远不会被激活，导致相应的参数永远不会被更新（主要原因：
  （1）：初始化参数较差，发生的几率很小；
  （2）learning rate太高）

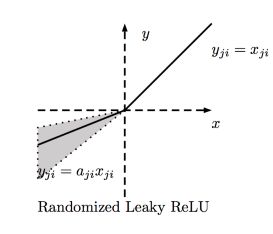
（4）Leaky ReLU函数（目前使用最为广泛和通用的activation function）
函数表达式：
$$f(x)=max(ax,x)$$
Leaky ReLU函数及其导数的图像：

Leakey Relu 函数图像

Leakey Relu 函数导数图像

解释：

为了解决Dead ReLU Problem，提出了将ReLU的前半段变为不为0的ax，通常a=0.01
看起来Leaky ReLU具有ReLU的优点，而且在一定的程度上克服了ReLU的缺点，但是在实际上通常还是习惯用ReLU，也没有完全证明Leaky ReLU总是优于ReLU

（5）ELU（exponential Linear Units）函数
函数表达式：
$$f(x)=\{\begin{array}{rcl}x& & ifx>0\\ a（e^x-1)）& & otherwise\end{array}$$
函数及其导数的图像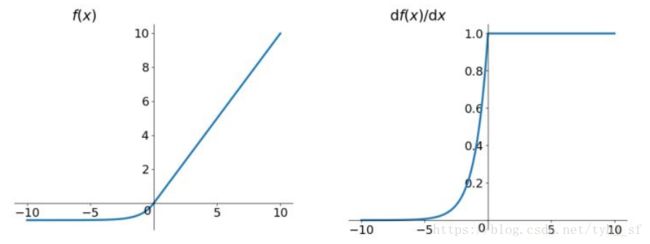

ELU函数及其导数

优点： >* 不存在Dead ReLU Problem >* 输出的均值接近于0，zero-centered

小问题：

计算量稍大

2） BP推导

定义变量:

推导过程：

1.网络初始化：
主要就是初始化各个连接权值w，值域于（-1,1）；设定误差函数e；给定计算精度值$ϵ$和最大学习次数M。

2.随机选择第k个输入样本和其对应的期望输出（即标签结果）

3.计算隐含层的各个神经元的输入和输出

4.利用网络期望输出和实际输出，计算误差函数e对输出层的各神经元的偏导数

5.利用隐藏层到输出层的连接权值、隐含层的输出值、输出层的偏导数计算出误差函数对隐含层各神经元的偏导数

6.根据输出层各神经元的${\delta }_o(k)$和隐含层各神经元的输出来修正连接权值$w_{ho}(k)$

7.利用隐含层各神经元的${\delta }_o(k)$和输入层的输出层的连接权

8.计算全局误差：

9.判断误差或者迭代次数是否满足要求，当误差在一定的精度范围之内或者达到迭代次数结束循环。否则返回到第三步重复进行下一轮学习。

4. 代码实现

import math
import random
import numpy as np
import matplotlib.pyplot as plt
random.seed(0)  # random加种子，让每次生成的随机数都是相同的
def rand(a, b):
    '''随机函数'''
    return (b - a) * random.random() + a


def make_matrix(m, n, fill=0.0):
    # 方法1,：直接使用numpy的zeros函数
    return np.zeros([m,n]).tolist()

    #方法2：定义list，逐行加入
    #     mat = []
    #     for i in range(m):
    #         mat.append([fill] * n)
    #     return mat

def sigmoid(x):
    '''sigmoid激活函数'''
    return 1.0 / (1.0 + math.exp(-x))


def sigmoid_derivative(x):
    '''sigmoid函数的导数'''
    return x * (1 - x)


class BPNeuralNetwork:
    def __init__(self):
        self.input_n = 0           # 初始化输入层神经元数
        self.hidden_n = 0          # 初始化隐含层神经元数
        self.output_n = 0          # 初始化输出层神经元数
        self.input_cells = []      # 初始化输入层神经元
        self.hidden_cells = []     # 初始化隐含层神经元
        self.output_cells = []     # 初始化输出层神经元
        self.input_weights = []    # 输入层到隐含层的权重
        self.output_weights = []   # 隐含层到输出层的权重
        self.input_correction = [] # 输入层校正值
        self.output_correction = [] # 输出层的校正值

    def setup(self, ni, nh, no):
        '''
        ni——输入层神经元的个数
        nh——隐含层神经元的个数
        no——输出层神经元的个数
        
        '''
        self.input_n = ni + 1      #加上一列偏置值
        self.hidden_n = nh
        self.output_n = no
        # init cells
        self.input_cells = [1.0] * self.input_n   # 初始化1行ni+1列的单位矩阵
        self.hidden_cells = [1.0] * self.hidden_n # 初始化1行nh列的单位矩阵
        self.output_cells = [1.0] * self.output_n # 初始化1行no列的单位矩阵
        # 初始化输入层到隐含层之间的权重
        self.input_weights =(np.random.random([self.input_n,self.hidden_n])-0.8)
        # 初始化输入层到隐含层之间的权重
        self.output_weights =(np.random.random([self.hidden_n,self.output_n]))*2 
        # 初始化校正矩阵
        self.input_correction = make_matrix(self.input_n, self.hidden_n)
        self.output_correction = make_matrix(self.hidden_n, self.output_n)

    def predict(self, inputs):
        # 激活输出层神经元
        for i in range(self.input_n - 1):
            self.input_cells[i] = inputs[i]
        # 激活隐含层神经元
        for j in range(self.hidden_n):
            total = 0.0
            for i in range(self.input_n):
                total += self.input_cells[i] * self.input_weights[i][j]
            self.hidden_cells[j] = sigmoid(total)
        # 激活输出层神经元（即输出结果）
        for k in range(self.output_n):
            total = 0.0
            for j in range(self.hidden_n):
                total += self.hidden_cells[j] * self.output_weights[j][k]
            self.output_cells[k] = sigmoid(total)
        return self.output_cells[:]

    def back_propagate(self, case, label, learn, correct):
        '''
        case——输入数据
        label——标签数据
        learn——学习率
        correct——校正参数
        '''
        # 正向传参
        self.predict(case)
        # 获取输出层误差及误差相对于输出层神经元的偏导数
        output_deltas = [0.0] * self.output_n
        for o in range(self.output_n):
            error = label[o] - self.output_cells[o]
            output_deltas[o] = sigmoid_derivative(self.output_cells[o]) * error
        # 获取隐含层的相对误差及其相对于隐含层神经元的偏导数
        hidden_deltas = [0.0] * self.hidden_n
        for h in range(self.hidden_n):
            error = 0.0
            for o in range(self.output_n):
                error += output_deltas[o] * self.output_weights[h][o]
            hidden_deltas[h] = sigmoid_derivative(self.hidden_cells[h]) * error
        # 更新隐含层到输出层的权值
        for h in range(self.hidden_n):
            for o in range(self.output_n):
                change = output_deltas[o] * self.hidden_cells[h]
                self.output_weights[h][o] += learn * change + correct * self.output_correction[h][o]
                self.output_correction[h][o] = change
        # 更新输入层到输出层的权重
        for i in range(self.input_n):
            for h in range(self.hidden_n):
                change = hidden_deltas[h] * self.input_cells[i]
                self.input_weights[i][h] += learn * change + correct * self.input_correction[i][h]
                self.input_correction[i][h] = change
        # 获取全局误差
        error = 0.0
        for o in range(len(label)):
            error += 0.5 * (label[o] - self.output_cells[o]) ** 2
        return error

    def train(self, cases, labels, limit=10000, learn=0.05, correct=0.1):
        for j in range(limit):
            error = 0.0
            for i in range(len(cases)):
                label = labels[i]
                case = cases[i]
                error += self.back_propagate(case, label, learn, correct)
            if j%100==0:   
                plt.scatter(j,error)
        plt.title('Error curve')
        plt.xlabel('iteration')
        plt.ylabel('error')
        plt.show()

    def test(self):
        cases = [
            [0, 0],
            [0, 1],
            [1, 0],
            [1, 1],
        ]
        labels = [[0], [1], [1], [0]]
        self.setup(2, 5, 1)
        self.train(cases, labels, 10000, 0.05, 0.1)
        for case in cases:
            print(self.predict(case))


if __name__ == '__main__':
    nn = BPNeuralNetwork()
    nn.test()

结果：

输出结果：

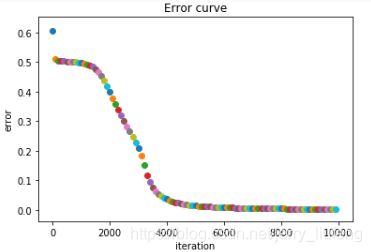
误差迭代图：

说明：

在迭代到1400次的时候误差明显开始降低，迭代到4000次的时候误差降低不太明显。（不同的初始化参数其下降的效率不同）

来都来了，点个赞给个建议再走呗