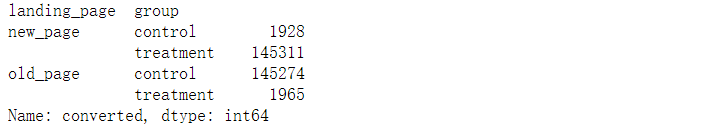Python数据分析案例-利用AB test分析转化率是否存在差异

1. AB test简介

AB测试是为Web或App界面或流程制作两个（A/B）或多个（A/B/n）版本，在同一时间维度，分别让组成成分相同（相似）的访客群组（目标人群）随机的访问这些版本，收集各群组的用户体验数据和业务数据，最后分析、评估出最好版本，正式采用。

方法通俗讲就是控制变量，然后通过统计学中的假设检验来分析来自两个或多个组样本均值的差异性，从而判断它们各自代表的总体的差异是否显著。

2. 案例

2.1 背景

案例数据为对网页新、旧页面的AB测试结果，目标是判断两版页面的日转化率是否存在显著区别。
数据来源：点击链接

2.2 数据清洗

数据导入

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from scipy import stats
plt.rcParams['font.sans-serif'] = ['SimHei']  
plt.rcParams['axes.unicode_minus'] = False 
# 加载数据集
df = pd.read_csv('ab_data.csv')
df.head()

# 加载用户国家分布数据集
df1 = pd.read_csv('countries.csv')
df1.head()

去重

# 去重
df.drop_duplicates( inplace=True)

合并

# 合并
data = df.merge(df1, on='user_id', how='inner')
data.head()

查看新旧两组页面成分

# 查看两组的页面成分
data.groupby(['landing_page','group']).converted.count()

• 可以看到新网页中有对照组和旧网页中有实验组，删去这部分数据

# 删除实验组中的旧网页与对照组中的新网页
data = data.query("(group == 'control' & landing_page == 'old_page') | (group == 'treatment' & landing_page == 'new_page')")

检验

# 再次查看两组的页面成分---已全部删除
data.groupby(['landing_page','group']).converted.count()

• 可以看到已删除实验组中的旧网页与对照组中的新网页

# 查看user_id重复项
data.user_id.value_counts().loc[data.user_id.value_counts() >1]

删除重复的用户id，保留最近的一条记录

# 删除重复值
data.drop_duplicates('user_id', keep = 'last', inplace = True)

时间格式转换

# 由于不清楚数据集的背景，所以将美国和加拿大的时间转换为美国中部时区时间，平衡下美国五个时区的时差，英国则无需转换
# 此转换操作是否合适待讨论
data['date'] = pd.to_datetime(data.timestamp.tolist(), utc=True).strftime("%Y-%m-%d")
data['date'].loc[data.query("country !='UK'").index] = pd.to_datetime(data.query("country !='UK'").timestamp.tolist(), utc=True).tz_convert("US/Central").strftime("%Y-%m-%d")

• 数据清洗完毕

2.3 数据分析

查看总体转化率

# 查看总体转化率
data.converted.mean()

• 总体转化率：0.11959708724499628

查看实验组与对照组的转化率

# 查看实验组与对照组的转化率
data.groupby(['group']).converted.mean()

• 对照组的总体转化率较高

查看每日的转化率对比

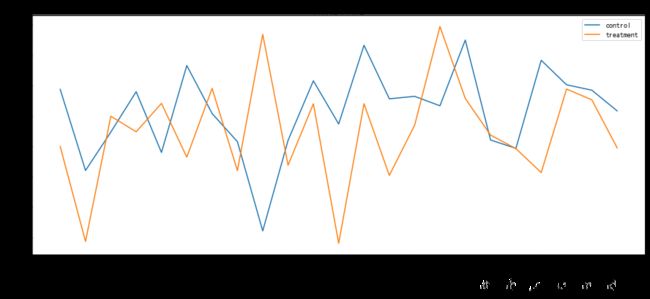
# 查看每日的转化率对比
fig,ax = plt.subplots(figsize=(15, 6))
ax.plot(data.query("group =='control'").groupby('date').converted.mean(), label='control')
ax.plot(data.query("group =='treatment'").groupby('date').converted.mean(), label='treatment')
ax.tick_params(axis='x', which='major', labelrotation=60)
ax.set_title("日转化率对比")
ax.legend()
plt.show()

• 从上图可以看到，对照组与实验组每日的转化率有一定的波动

为避免辛普森悖论，将转化率细分到国家进行对比

# 分别查看每个地区的总体转化率对比
data.groupby([ 'country','group']).converted.agg({
     'count', 'mean'})

观察上表：

• 总体转化率日实验组低于对照组，加拿大与美国与其一致；而英国相反，实验组较高。
• 三个国家的样本量不均匀。

避免新奇效应，细分到每天进行观察

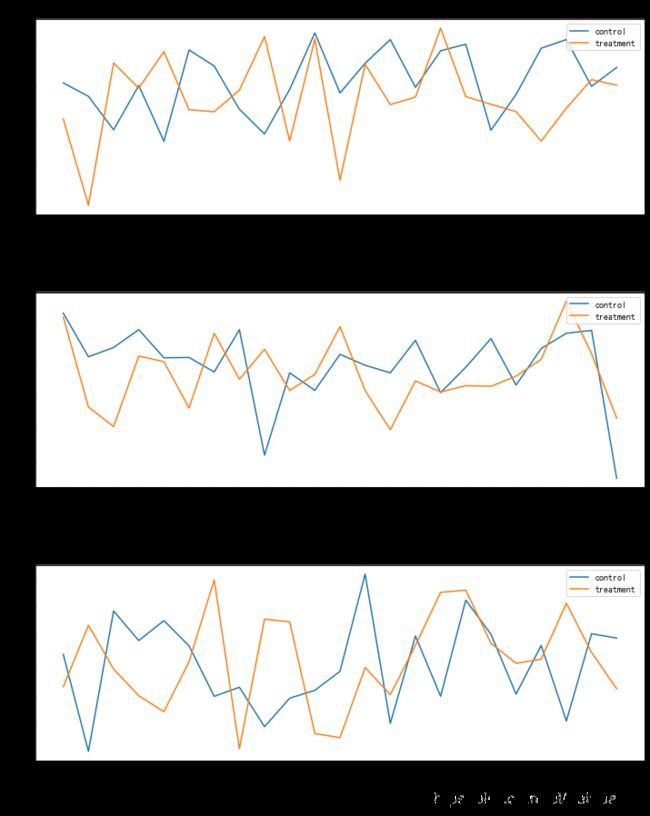
# 分别查看每个地区每日的转化率对比
fig,ax = plt.subplots(ncols=1, nrows=3, figsize=(12, 15))
for i,j in enumerate(data.country.unique()):
    ax[i].plot(data.query("group =='control' & country == @j").groupby('date').converted.mean(), label='control')
    ax[i].plot(data.query("group =='treatment' & country == @j").groupby('date').converted.mean(), label = 'treatment')
    ax[i].tick_params(axis='x', which='major', labelrotation=60)
    ax[i].legend(loc='upper right')
    ax[i].set_title(j)
    plt.subplots_adjust(hspace =0.4)
plt.show()

细分到每日进行对比后：

• 美国与英国的两组转化率起伏相对较小
• 加拿大的两组数据波动较大，对照组的最后一天转化率可能存在异常

查看样本量，避免数量不均衡带来的影响

data.groupby(['country', 'group','date']).converted.count().unstack().T

• 从上表可以看到，除去第一天和最后一天，其余的天数各国均分配较均匀。可能与之前的转换的时区有关？我尝试了多数的时区，也没能减少一天，so，如果有人解决这个问题的话，若能留言告知不胜感激。
• 加拿大最后一天的数量较少，可能是其对照组转化率较差的原因，所以剔除掉最后一天的数据。

2.4 假设检验

2.4.1 独立双样本t检验

问题：

• 实验组与对照组的日转化率是否有差异

零假设与备择假设：

• H0：实验组与对照组的日转化率没有差异，U0 = U1
• H1: 实验组与对照组的日转化率有差异， U0 ≠ U1

检验类型：

• 样本量n=22，小于30, 选择独立双样本t检验，双尾

显著性水平选取：

• p值选取0.05

2.4.1.1 正态性检验

# 剔除最后一天的数据
data =data.query("date != '2017-01-24'")
# 对照组的日转化率
control_DCVR = data.query("group == 'control'").groupby('date').converted.mean()
# 实验组的日转化率
treatment_DCVR = data.query("group == 'treatment'").groupby('date').converted.mean()

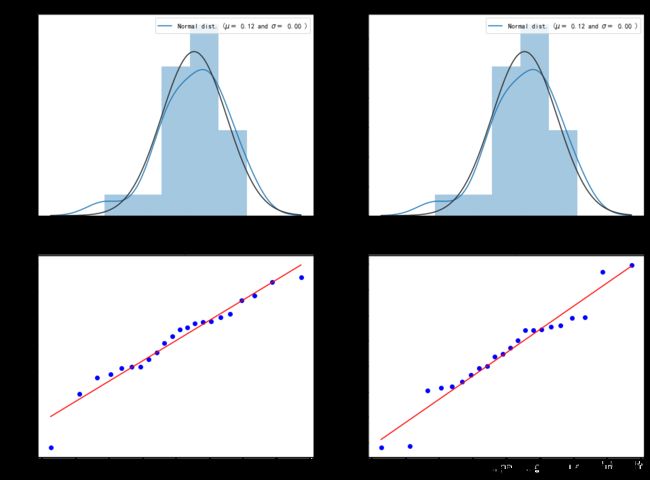
查看核密度估计图和QQ图

# 查看核密度估计图
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(16, 12))
title_list = ['control', 'treatment']
for i,j in enumerate([control_DCVR, treatment_DCVR]):
    sns.distplot(control_DCVR, fit=stats.norm, ax=ax[0][i])
    (mu, sigma) = stats.norm.fit(j)
    ax[0][i].legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],loc='best')
    ax[0][i].set_title(title_list[i])
    stats.probplot(j, plot=ax[1][i])

两组数据大致符合正态分布

Shapiro-Wilk检验正态性

print('control Shapiro-Wilk test p-value:', stats.shapiro(control_DCVR).pvalue)
print('treatment Shapiro-Wilk test p-value:', stats.shapiro(treatment_DCVR).pvalue)

结果：

• control Shapiro-Wilk test p-value: 0.4410777688026428

• treatment Shapiro-Wilk test p-value: 0.37171587347984314

• Shapiro-Wilk检验 原假设为指定数据服从正态分布

• p值均大于0.05，不能拒绝原假设，说明对照组与实验组数据均符合正态分布

2.4.1.2 方差齐性检验

# levene test
print('levene test p-value:', stats.levene(control_DCVR, treatment_DCVR, center='mean').pvalue)

结果：

• levene test p-value: 0.5175103523245008

• levene检验 原假设为两独立样本来自的总体方差相等

• p值大于0.05，不能拒绝原假设，认为对照组与实验组数据均具有齐次性

满足t检验的前提条件，于是接下来进行t检验

2.4.1.3 t检验

import statsmodels.stats.weightstats as sw
t_value, p_value, df = sw.ttest_ind(control_DCVR, treatment_DCVR)
print('t值：{}\np值：{}\n自由度：{}'.format(t_value, p_value, df))

结果：

• t值：1.323987309557865
• p值：0.19266812808059422
• 自由度：42.0

结论：

• p值大于0.05，不能拒绝原假设，所以认为实验组与对照组的日转化率没有差异。

2.4.2 Kruskal-Wallis检验

问题：

• 各国的实验组与对照组的日转化率是否有差异

检验类型：

• 若能通过正态性检验和方差齐性检验，使用多因素方差分析，没有通过则使用非参检验—Kruskal-Wallis检验

查看每个国家日转化率的相关统计量

# 描述统计
(data.groupby(['group', 'country', 'date'])
     .converted
     .mean()
     .reset_index()
     .groupby(['group', 'country'])
     .converted
     .agg({
     'mean', 'std', 'count'})
     .round(4)
)

• 对照组中：美国的日均转化率最高
• 实验组中：英国的日均转化率最高

正态性检验

# 正态性检验
data_temp = data.groupby(['group', 'country', 'date']).converted.mean().unstack([0,1])
for i in data_temp.columns:
    print('{} {} Shapiro-Wilk test p-value:'.format(i[0], i[1]), stats.shapiro(data_temp[i]).pvalue)

• 默认p值为0.05，所以加拿大的对照组数据没有通过正态性检验

查看加拿大对照组数据的峰度与偏度

print('control CA kurtosis: ', abs(data_temp[('control', 'CA')].kurtosis()))
print('control CA skew: ', abs(data_temp[('control', 'CA')].skew()))

• 一般来讲，如果峰度绝对值小于10并且偏度绝对值小于3，则说明数据虽然不是绝对正态，但基本可接受为正态分布。
• 加拿大的对照组数据其峰度与偏度绝对值满足要求。

方差齐性检验

# levene test---测试对照组各国间的方差齐性
print('levene test between control group p-value:',stats.levene(*data_temp.T.values[:3], center='mean').pvalue)
# 测试实验组各国间的方差齐性
print('levene test between treatment group p-value:',stats.levene(*data_temp.T.values[3:], center='mean').pvalue)

• p值小于0.05，没有通过方差齐性测试，认为至少存在一组数据与其他数据方差不齐，所以接下来使用Kruskal-Wallis检验

零假设与备择假设：

• H0：各国实验组与对照组的日转化率没有差异，U0 = U1 = U2
• H1: 各国实验组与对照组的日转化率有差异， U0, U1, U2不全相等

显著性水平选取：

• p值选取0.05

Kruskal-Wallis检验

stats.kruskal(*data_temp.T.values)

结论：

• p值大于0.05，不能拒绝原假设，认为各国实验组与对照组的日转化率没有差异，并且无需事后多重检验。

2.5 结论

经过检验，新旧两版本网页的日转化率没有显著性差异，各国两版本网页的日转化率也没有显著性差异。