生存分析及R语言实现(三)：Cox模型及R实现

本系列旨在对生存分析及在R中的实践进行介绍，主要侧重理解与应用。由于参考的是英文文献，所以许多名词都直接用了英文，以免翻译有误给大家造成误解。文中错误之处欢迎批评指正。

本文介绍的模型全称为：Cox比例风险回归模型(Cox Proportional Hazards Regression Model)，为简便起见，在不引起歧义的情况下我们称之为Cox模型。

1.1 模型建立

1.1.1 模型假设

引入$p$维随机向量$Z\in {\mathbb{R}}^p$，用于表示协变量(解释变量)，可能表示我们感兴趣的患者用药情况、性别、年龄等特征。考虑条件危险率函数：
$$\lambda (t|Z)\mathrm{d}t=\mathrm{Pr}[t\le T<t+\mathrm{d}t|T\ge t,Z].$$

我们之前介绍过生存分析中的模型：
$$\mathrm{d}N(t)=\mathbb{I}[X\ge t]\lambda (t)\mathrm{d}t+\mathrm{d}M(t),$$
其中$N(t)=\mathbb{I}[X\le t,\delta =1]$，$M(t)$为鞅残差。

现在我们引入了$Z$,那么$\lambda (t)$就变为$\lambda (t|Z)$。Cox模型对其形式作出假设：
$$\lambda (t|Z)={\lambda }_0(t)\exp ({\beta }^{T}Z),$$
其中$\beta \in {\mathbb{R}}^p$是$p$维参数，${\lambda }_0(t)$是基线危险率函数。

该模型很重要的特点是，不同$Z$值对应的$\lambda (t|Z=z)$的比例，是不随时间变化的。也就是，考虑$Z=z_i$和$Z=z_j$这两个不同的小组(这里$z_i$和$z_j$都是$p$维向量)，则
$$\frac{\lambda (t|Z=z_j)}{\lambda (t|Z=z_i)}=\exp ({\beta }^T(z_j-z_i))$$

1.1.2 参数化${\lambda }_0(t)$与极大似然估计

上文提到的模型中，我们可以参数化${\lambda }_0(t)$，使之变成一个具体的函数。比如
$${\lambda }_0(t;\eta )=\alpha {\gamma }^{-\alpha }{t}^{\alpha -1},$$
其中$\eta =(\alpha ,\gamma {)}^T$称为冗余参数(nuisance parameter)。

有了具体的${\lambda }_0(t)$之后，我们就可以求参数的极大似然估计(MLE)。因为现在模型是基于$Z$，因此我们可以放宽对独立性的限制，仅假设删失时间$C$和事件发生时间$T$条件独立，即
$$C\perp T|Z.$$

假设我们观测到一组数据
$$(X_i,{\delta }_i,Z_i),i=1,\cdots ,n,$$

可以通过对令分数函数(score function)等于零的方式得到参数$\theta =(\beta ,\eta )$的极大似然估计。略过中间计算过程，极大似然估计为如下方程的解：

$$n^{-1}\sum _{i=1}^n\{{\int }_0^{\infty }[Z_i^T,\frac{\partial }{\partial {\eta }^T}\log {\lambda }_0(t;\eta ){]}^T\mathrm{d}{M}_t(t;\theta )\}=0$$

1.2.3 R语言求解

在survival包里的coxph函数可用于求Cox模型的参数估计、置信区间等。例如：

library(survival)
mod = coxph(Surv(time, status) ~., data = rats)
summary(mod)

1.2 偏似然函数(Partial Likelihood Function)

假设事件只在离散的时刻$t_1<t_2<\cdots <t_m$时发生，且每个$t_j$只有一个个体有事件发生。用 $\mathcal{R}(t_j)=\{i:X_i\ge t_j\}$ 代表在$t_j$仍“有风险”的个体数量，也就是$t$时刻既没有发生outcome event(如死亡，肿瘤)也没有删失的个体数。
那么对于$t_j$时刻而言，每个个体partial likelihood (偏似然，或部分似然)定义为
$$P{L}_j=\mathrm{Pr}[该个体在t_j发生事件|在\mathcal{R}(t_j)中，t_j时刻有一人发生事件]$$
我们用$Z_{(}j)$表示$t_j$时刻发生事件的个体的解释变量，则
$$P{L}_j=\frac{\lambda (t)j|Z_{(}j)\mathrm{d}t}{{\sum }_{i\in \mathcal{R}(t_j)}\lambda (t_j|Z_i)\mathrm{d}t}=\frac{\exp ({\beta }^T{Z}_j)}{{\sum }_{i\in \mathcal{R}(t_j)}\exp ({\beta }^T{Z}_i)}$$

于是对$n$组观测$(X_i,{\delta }_i,Z_i$，偏似然函数为
$$P{L}_n(\beta )=\prod _{j=1}^m\frac{\exp ({\beta }^T{Z}_{(j)})}{{\sum }_{i\in \mathcal{R}}\exp ({\beta }^T{Z}_i)}.$$

则$\beta$的极大偏似然函数估计(Maximum Partial Likelihood Estimation,简称MPLE)为：
$${\hat{\beta }}_{MPLE}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}P{L}_n(\beta )$$

1.3 Breslow估计

1.3.1 理论推导

通过前文的模型我们知道，给定解释变量$Z$后的生存函数$S(t)$可写作:
$$S(t|Z=z;\beta ,{\Lambda }_0)=\exp (-\exp ({\beta }^{T}z){\Lambda }_0(t))$$
因此我们只需找到${\Lambda }_0(t)$的估计，就可以估计$S(t|Z=z;\beta ,{\Lambda }_0)注意到$$\mathbb{E}[d{M}_i(t;\beta ,{\Lambda }_0)]=0,$$于是有
$$\mathrm{d}{\Lambda }_0(t)=\frac{\mathbb{E}[\mathrm{d}{N}_i(t)]}{\mathbb{E}[\mathbb{I}(X_i\ge t)]\exp ({\beta }^T{Z}_i)}$$
对cumulative hazard function ${\Lambda }_0(t)$的Breslow估计即为
$${\hat{\Lambda }}_0(t)={\int }_0^t\frac{{\sum }_{i=1}^n\mathrm{d}{N}_i(s)}{{\sum }_{i=1}^n\mathbb{I}(X_i\ge s)\exp (\widehat{{\beta }^T{Z}_i})}$$
将其带入$S(t|Z;\beta ,{\Lambda }_0)$即可得到$\hat S(t|Z;\beta,\Lambda_0) $

1.3.2 R语言求Breslow估计

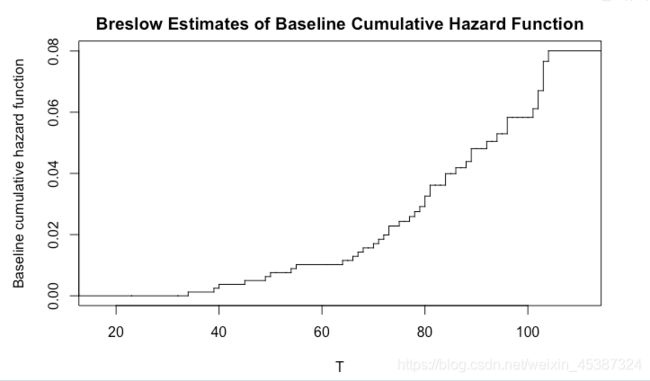
可以将basehaz函数作用于coxph对象，得到${\hat{\Lambda }}_0$，其包括time和hazard两个变量，其曲线如图：

Lambda0 = basehaz(mod)

plot(stepfun(Lambda0$time,c(0,Lambda0$hazard)), do.points = FALSE,
     xlab = 'T',ylab = 'Baseline cumulative hazard function', main = 'Breslow Estimates of Baseline Cumulative Hazard Function')

1.4 残差分析

这里我们考虑此前提及的鞅残差(Martingale Residual)。与普通线性回归模型类似，如果数据满足Cox模型假设的话，鞅残差应当是随机分布在0左右，没有明显的趋势或形状。在R中可以用resid作用在coxph对象上获取残差：

mod = coxph(Surv(time,status)~ph.ecog+age, data = lung)
martingale.resid = resid(mod,type = 'martingale')